- 2022-09-06 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
初中数学竞赛精品标准教程及练习(67)
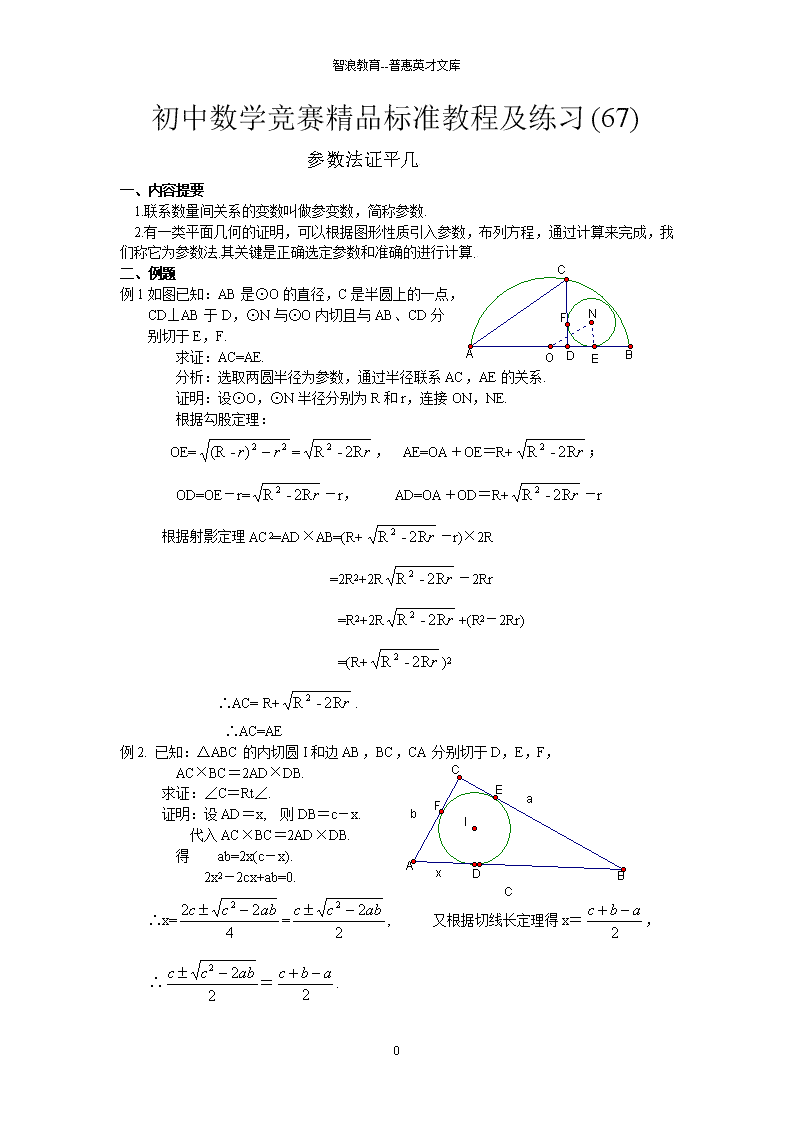
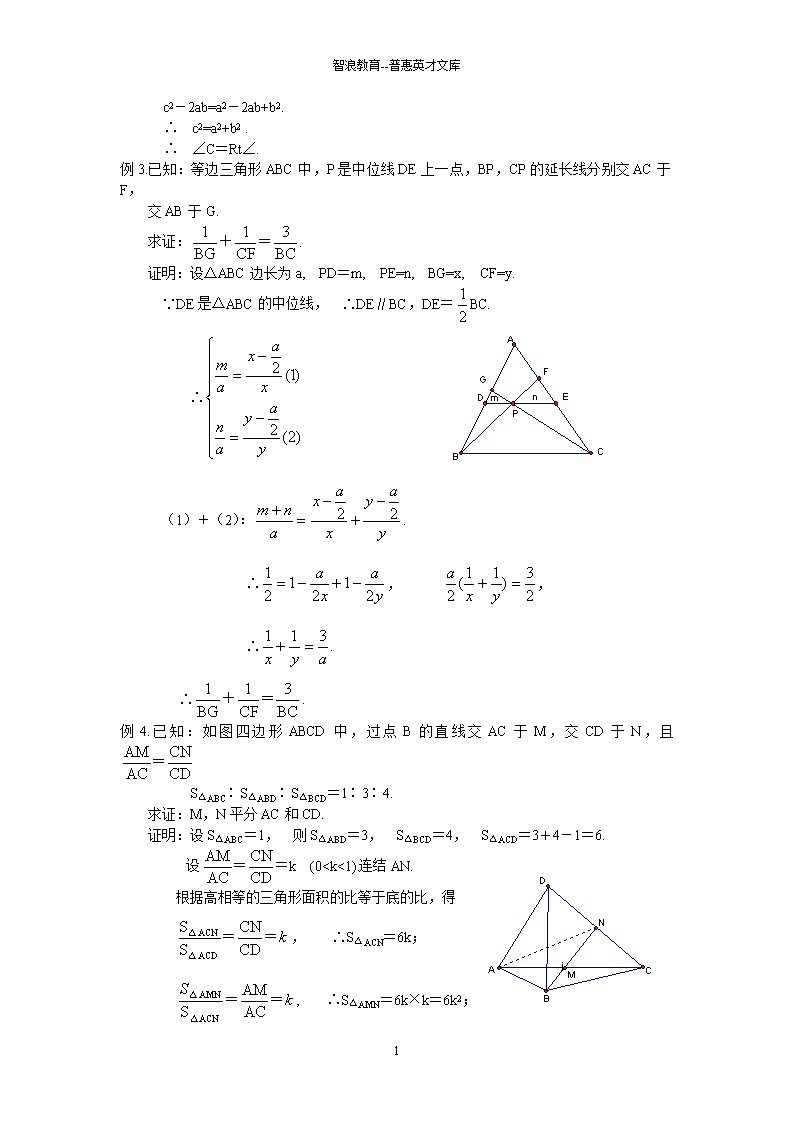
智浪教育--普惠英才文库初中数学竞赛精品标准教程及练习(67)参数法证平几一、内容提要1.联系数量间关系的变数叫做参变数,简称参数.2.有一类平面几何的证明,可以根据图形性质引入参数,布列方程,通过计算来完成,我们称它为参数法.其关键是正确选定参数和准确的进行计算.二、例题例1如图已知:AB是⊙O的直径,C是半圆上的一点,CD⊥AB于D,⊙N与⊙O内切且与AB、CD分别切于E,F.求证:AC=AE.分析:选取两圆半径为参数,通过半径联系AC,AE的关系.证明:设⊙O,⊙N半径分别为R和r,连接ON,NE.根据勾股定理:OE==,AE=OA+OE=R+;OD=OE-r=-r, AD=OA+OD=R+-r根据射影定理AC2=AD×AB=(R+-r)×2R =2R2+2R-2Rr=R2+2R+(R2-2Rr)=(R+)2∴AC=R+. ∴AC=AE例2.已知:△ABC的内切圆I和边AB,BC,CA分别切于D,E,F,AC×BC=2AD×DB.求证:∠C=Rt∠.证明:设AD=x, 则DB=c-x.代入AC×BC=2AD×DB.得 ab=2x(c-x).2x2-2cx+ab=0.∴x==, 又根据切线长定理得x=,∴=. 4\n智浪教育--普惠英才文库c2-2ab=a2-2ab+b2.∴ c2=a2+b2.∴ ∠C=Rt∠.例3.已知:等边三角形ABC中,P是中位线DE上一点,BP,CP的延长线分别交AC于F,交AB于G.求证:.证明:设△ABC边长为a, PD=m, PE=n, BG=x, CF=y.∵DE是△ABC的中位线, ∴DE∥BC,DE=BC.∴ (1)+(2):.∴, , ∴.∴.例4.已知:如图四边形ABCD中,过点B的直线交AC于M,交CD于N,且S△ABC∶S△ABD∶S△BCD=1∶3∶4.求证:M,N平分AC和CD.证明:设S△ABC=1, 则S△ABD=3, S△BCD=4, S△ACD=3+4-1=6.设=k(0查看更多
相关文章
- 当前文档收益归属上传用户