- 2022-09-06 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省初中升学数学练习题
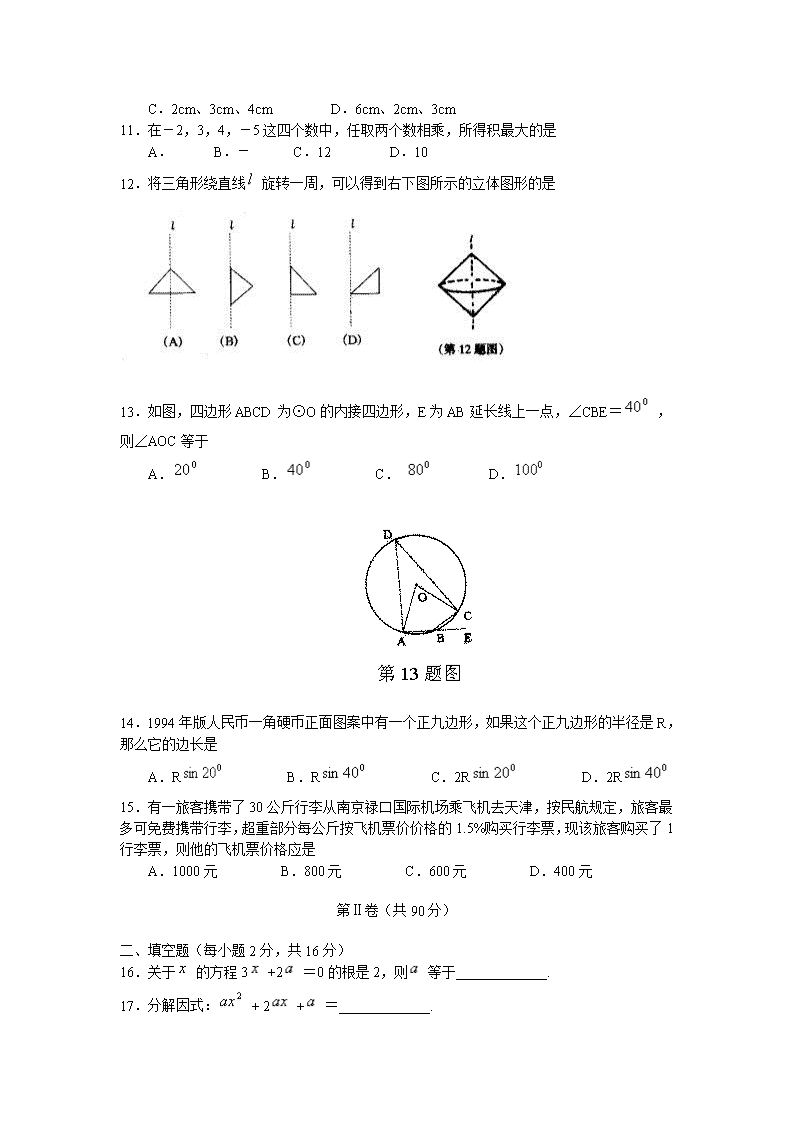
江苏省初中升学数学练习题 第Ⅰ卷(30分)一、选择题(下列各题所附的四个选项中,有且只有一个是正确的,每小题2分,共30分)1.-2的相反数是 A.-2 B.2 C. D.2.我国最长的河流长江全长约为6300千米,用科学记数法表示为 A.63×102千米 B.6.3×102千米 C.6.3×103千米 D.6.3×104千米3.计算的结果是 A.-9 B.9 C. D.4.的一个有理化因式是 A. B. C. D.5.下列二次根式中,与是同类二次根式的是 A. B. C. D.6.的化简结果是 A.2 B.-2 C.2或-2 D.47.已知在Rt△ABC中,∠C=,=,则的值等于 A. B. C. D.8.如果两个等腰直角三角形斜边的比是1:2,那么它们面积的比是 A.1:1 B.1: C.1:2 D.1:49.人数相等的甲、乙两班学生参加了同一次数学测验,班级均分和方差如下:=80,=80,=240,=180,则成绩较为整齐的是 A.甲班 B.乙班 C.两班一样整齐 D.无法确定10.有下列长度的三条线段,能组成三角形的是 A.1cm、2cm、3cm B.1cm、4cm、2cm\n C.2cm、3cm、4cm D.6cm、2cm、3cm11.在-2,3,4,-5这四个数中,任取两个数相乘,所得积最大的是 A. B.- C.12 D.1012.将三角形绕直线旋转一周,可以得到右下图所示的立体图形的是13.如图,四边形ABCD为⊙O的内接四边形,E为AB延长线上一点,∠CBE=,则∠AOC等于 A. B. C. D.14.1994年版人民币一角硬币正面图案中有一个正九边形,如果这个正九边形的半径是R,那么它的边长是 A.R B.R C.2R D.2R15.有一旅客携带了30公斤行李从南京禄口国际机场乘飞机去天津,按民航规定,旅客最多可免费携带行李,超重部分每公斤按飞机票价价格的1.5%购买行李票,现该旅客购买了1行李票,则他的飞机票价格应是 A.1000元 B.800元 C.600元 D.400元第Ⅱ卷(共90分)二、填空题(每小题2分,共16分)16.关于的方程3+2=0的根是2,则等于_____________.17.分解因式:+2+=_____________.\n18.用换元法解方程-+6=0,若设=,则原方程变为 ___________________.19.如图,矩形ABCD中,A(-4,1),B(0,1)C(0,3),则D点坐标是(_____)京长江二桥连续七天的车流量(每日过桥车辆次数)分别为(单位:千辆/日) :.这七天平均车流量为_____________千辆/日.21.请写出两个既是轴对称图形,又是中心对称图形的正多边形:_____________.22.在△ABC中,AB=AC,∠BAC=1⊙A与BC相切于D,与AB相交于E,则∠ADE等于 _____________度.23.已知⊙O的半径为4cm,AB是⊙O的弦,点P在AB上,且OP=2cm,PA=3cm,则 PB=__________cm.三、解下列各题(每小题5分,共24.计算:+.25.解不等式组,并写出不等式组的整数解.26.已知:关于的方程+-1=0.(1)求证:方程一定有两个不相等的实数根;(2)若方程的两根分别为、,且=2,求的值.27.在某一电路中,保持电压不变,电流(安培)与电阻(欧姆)成反比例,当电阻=5欧姆时,电流=2安培。(1)求与之间的函数关系式;\n(2)当电流=0.5安培时,求电阻的值.四、(本题6分)28.以长为2的定线段AB为边作正方形ABCD,取AB的中点P,连结PD,在BA的延长线上取点F, 使PF=PD,以AF为边作正方形AMEF,点M在AD上,如图所示. (1)求AM、DM的长; (2)求证:AM2=AD·DM.五、(本题7分)29.如图,AB是⊙O的直径,P在AB的延长线上,PD与⊙O相切于D, C在⊙O上,PC=PD. (1)求证:PC是⊙O的切线; (2)连结AC,若AC=PC,PB=1,求⊙O的半径.六、(本题7分)30.某医药研究所开发了一种新药,在试验药效时发现,如果成人按规定剂量服用,那么服药后2小时时血液中含药量最高,达每毫升6微克(1微克=毫克),接着逐步衰减,10小时时血液中含药量为每毫升3微克,每毫升血液中含药量(微克)随时间(小时)的变化如图所示.当成人按规定剂量药后,(1)分别求出≤2和≥2时与之间的函数关系式;(2)如果每毫升血液中含药量为4微克或4微克以上时 在治疗疾病时是有效的,那么这个有效时间是多长?七、(本题7分)31.如图1,在平面上,给定了半径为的圆O,对于任意点P,在射线OP上取一点P′,使得OP·OP′=,这种把点P变为点P′的变换叫做反演变换,点P与点P′叫做互为反演点. (1)如图2,⊙O内外各一点A和B,它们的反演点分别为A′和B′, 求证:∠A′=∠B;(2)如果一个图形上各点经过反演变换得到的反演点组成另一个图形,那么这两个图形叫做互为反演图形. ①选择:如果不经过点O的直线与⊙O相交,那么它关于⊙O的反演图形是().\n A.一个圆 B.一条直线 C.一条线段 D.两条射线 ②填空:如果直线与⊙O相切,那么它关于⊙O的反演图形是_________,该图形与圆O的位置关系是______________.八、(本题8分)32.某农户种植花生,原来种植的花生亩产量为克,出油率为50%(即每100千克花生可加工成花生油50千克).现在种植新品种花生后,每亩收获的花生可加工成花生油132千克,其中花生出油率的增长率是亩产量的增长率的.求新品种花生亩产量的增长率.九、(本题8分)33.如图,E、F分别是边长为4的正方形ABCD的边BC、CD上的点,CE=1,CF=,直线FE交AB的延长线于G.过线段FG上的一个动点H作HM⊥AG,HN⊥AD,垂足分别为M、N.设HM=,矩形AMHN的面积为.(1)求与之间的函数关系式;(2)当为何值时,矩形AMHN的面积最大,最大面积是多少?十、(本题11分)34.(1)如图1,已知A点坐标为(0,3),⊙A的半径为1,点B在轴上. ①若B点坐标为(4,0),⊙B的半径为3,试判断⊙A与⊙B的位置关系; ②若⊙B过点M(2,0),且与⊙A相切,求B点坐标. (2)如图2,点A在轴上,⊙A在轴的上方.\n 问:能否在轴的正半轴上确定一点B,使⊙B与轴相切,并且与⊙A外切,为什么?江苏省初中升学数学练习题答案第I卷(30分)一、选择题(每小题2分,共30分)题号123456789101112131415答案BCDCAAADBCCBCCB第II卷(90分)二、填空题(每小题2分,共16分)16.-3 17. 18.-+6=0 19.-4,3 .521.边数为偶数的两个正多边形(例如正方形和正六边形) 22.60 23.4三、解下列各题(每小题5分,共24.(本题5分)解:原式= (2分) =(3分) =(5分)25.(本题5分)解:解不等式2+5≤3(+2),得≥-1. 解不等式<,得<3. (3分) ∴原不等式组的解集是-1≤<3. (4分) ∴不等式组的整数解是:-1,0,1,2. (5分)26.(本题5分)(1)证明:△=+4. (1分) ∵≥0,∴+4>0.即△>0. ∴方程一定有两个不相等的实数根. (2分)(2)解:∵、是方程的两根, (3分)\n ∴+=-,=-1. (3分) ∵=2-, ∴==2. ∴=2. ∴=2. (5分)27.(本题5分)解:(1)设=.(1分) 当R=5时,=2,可得=10. (2分) ∴=. (3分) (2)当=0.5时,可得R=姆). (5分)四、(本题6分)28.(1)解:∵正方形ABCD边长为2,P是AB中点, ∴AB=AD=2,AP=1,∠BAD=90O. ∴PD=. (1分) ∵PF=PD,∴AF=-1. 在正方形AMEF中,AM=AF=-1. (2分) MD=AD-AM=3-. (3分)(2)证明:由(1),得 AD·DM=2(3-)=6-2, (4分) AM2=(-1)2=6-2. (5分) ∴AM2=AD·DM.(6分)五、(本题7分)29.(1)证明:连结OD、OC. (1分) ∵PC=PD,OC=OD,PO=PO, ∴△PCO≌△PDO. ∴∠PCO=∠PDO. (2分) ∵PD切⊙O于点D, ∴∠PDO=90O.∴∠PCO=90O. ∴PC是⊙O的切线. (3分)\n(2)解法一:连结BC. ∵AC=PC,∴∠A=∠CPA. ∵∠A=∠PCB,∴∠PCB=∠CPA. ∴∠CBA=2∠CPA=2∠A.BC=PB=1. (5分) ∵AB是⊙O的直径,∴∠ACB=90O. ∵3∠A=90O.∴∠A=30O. (6分) ∴AB=2BC=2. ∴⊙O的半径是1. (7分)解法二:同解法一,得BC=1. (5分) 设⊙O的半径是. ∵PC是⊙O的切线, ∴PC2=PB·PA=1·(1+2). 在Rt△ABC中,AC2=AB2—BC2=(2)2—1. (6分) ∴1·(1+2)=(2SS)2—1. ∴⊙O的半径=1. (7分)六、(本题7分)30.解:(1)设≤2时,=. (1分) 把(2,6)代入上式,得=3, ∴≤2时,=3.(2分) 设≥2时,=+. (3分) 把(2,6)、(10,3)代入上式,得=,=.∴≥2时,=-+. (4分) (2)把=4代入=3中,得= (5分) 把=4代入=-+中, 得=. (6分) ∴由正比例函数和一次函数的性质,得=-=-=6(小时). ∴这个有效时间是6小时. (7分)七、(本题7分)\n31.(1)证明:∵A、B的反演点分别是、, ∴=,=. ∴=.即. (1分) ∵∠O=∠O,∴△ABO∽△.(2分) ∴∠=∠. (3分) (2)①A. (5分) ②圆;内切. (7分)八、(本题8分)32.解:设新品种花生亩产量的增长率为. (1分) 根据题意,得 1+)·50%(1+)=132. (4分) 解得=0.2,=-3.2(不合题意,舍去). (7分) 答:新品种花生亩产量的增长率为 (8分)九、(本题8分)33.解:(1)∵正方形ABCD的边长为4,CE=1,CF=, ∴CF∥AG,BE=3. ∴,∴BG=4. (2分) ∵HM⊥AG,CB⊥AG,∴HM∥BE. ∴=,∴MG=. (4分) ∴. (5分) (2)∵== (7分) ∴当=3时,最大,最大面积是12. (8分)十、(本题11分)34.解:(1)①在Rt△AOB中,\n AB==5>1+3, ∴⊙A与⊙B外离. (2分) ②设B点坐标为(,0),显然<2.根据题意,得⊙B的半径为2-, 两圆圆心距AB==. 当两圆外切时,=(2-)+1. ∴=0,此时,B点坐标为(0,0) (4分) 当两圆内切时,=(2-)-1. ∴=-4此时,B点坐标为(-4,0). (6分)(2)答:能 设⊙A的半径为. 解法一: ①在轴的负半轴上截取OD=. ②连结AD. ③作AD的垂直平分线MN交轴于点B. ∴点B即为所求的点.(9分) 理由:连结AB交⊙A于点C. ∵MN垂直平分AD,∴AB=BD. ∵AB≥OA>OD, ∴BD>OD. ∴B点在轴正半轴上. ∴CB+=OB+.∴CB=OB. ∴AB=OB+. ∵OB⊥轴, ∴以OB长为半径的⊙B与⊙A外切,且与轴相切.(11分) 解法二: ①作AD⊥轴,交⊙A的右半圆于点D. ②连结OD,交⊙A于点C. ③连结AC,并延长AC交轴的正半轴于点B. ∴点B即为所求的点. 理由:∵AD⊥轴,BO⊥轴,∴AD∥BO.∴∠ADC=∠BOC. ∵AC=AD,∴∠ADC=∠ACD. 又∵∠ACD=∠BCO, ∴∠BOC=∠BCO.∴CB=OB. ∴AB=OB+.\n ∵BO⊥轴, ∴以OB长为半径的⊙B与⊙A外切,且与轴相切.(11分)查看更多