2016年初中数学能力达标练习07

2016年初中数学能力达标练习07

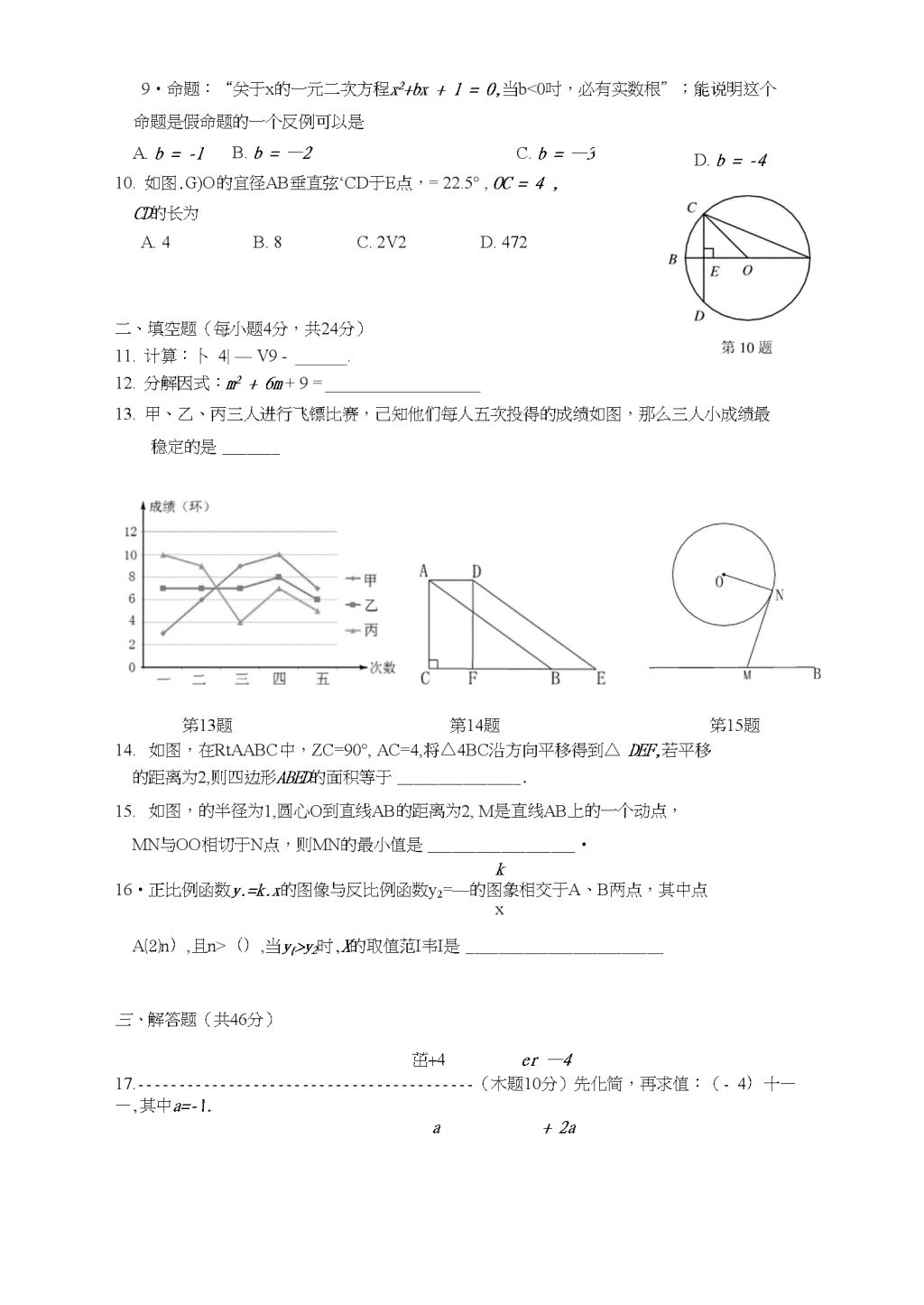
2016年初中数学能力达标练习（七）（满分：100分；考试时间：120分钟）一、选择题（每小题3分，共30分）1.-3的倒数是A.B.—C.3D.—3332.新亚欧人陆桥东起太平洋西岸屮国连云港，四达人西洋东岸荷兰鹿特丹等港口，横贯亚欧两人洲屮部地带，总长约为1090（）公里，1090（）用科学记数法表示为A.1.09xlO2B.1.09xlO3C.1.09X104D.0.109xl05A.ZA的平分线B.4C边的中线C.BC边的髙线D.AB边的乖直平分线3.一个不透明的盒了屮装启3个红球，2个黄球和1个绿球，这些球除了颜色外无其他差别,从中随机摸出一个小球，恰好是黄球的概率为1112A.一B.—C.—[)•一63234.卜-列计算错课的是.••A.3a/3-a/3=2V3B.x2-x3=x6C.-2+1-21=0D.(-3)-2=-5.如图,在AABC中，分別以点A,B为圆心，大于长为半径画弧，两弧分别交于点1）,E,6.小刚身高1・7m,测得他站立在阳光卜-的影子长为0.85m，紧接着他把手臂竖直举起，测D・2.2m得影子长为1.1m,那么小刚举起的手臂超出头顶A.0.5mB.0-55mC.0.6m7•如图，在正方体的平而展开图中A、B两点间的距离为6,折成正方体后4、〃两点是正方体的顶点，则这两个顶点的距离是A.3^23^2A\B.B第7题&如图，在MBC中，ZCAB=65°,在同一平面内，将\ABC绕点A逆时针旋转到\ABC的位置，使得CC//AB，则ZBAB等于A.50°B.60°C.65°D.70°\n9•命题：“关于x的一元二次方程x2+bx+l=0,当b<0吋，必有实数根”；能说明这个命题是假命题的一个反例可以是A.b=-lC.b=—3B.b=—210.如图.G)O的宜径AB垂直弦‘CD于E点，=22.5°,OC=4,CD的长为A.4B.8C.2V2D.472二、填空题（每小题4分，共24分）11.计算：卜4|—V9-.12.分解因式：m2+6m+9=D.b=-413.甲、乙、丙三人进行飞镖比赛，己知他们每人五次投得的成绩如图，那么三人小成绩最笫13题第14题笫15题稳定的是14.如图，在RtAABC中，ZC=90°,AC=4,将△4BC沿方向平移得到△DEF,若平移的距离为2,则四边形ABED的面积等于.15.如图，的半径为1,圆心O到直线AB的距离为2,M是直线AB上的一个动点，MN与OO相切于N点，则MN的最小值是•k16•正比例函数y.=k.x的图像与反比例函数y2=—的图象相交于A、B两点，其中点xA⑵n）,且n>（）,当y{>y2时,X的取值范I韦I是三、解答题（共46分）茁+4er—417.（木题10分）先化简，再求值：（-4）十——,其中a=-\.a+2a\n17.（本题10分）如图，直线y=kx+h经过A（-3,寸）、B（5,一4）两点，过点A作AD丄兀轴于£＞点，过点3作BC丄y轴于C点,断四边形BCDE的形状，并加以证明.19.（本题13分）已知二次函数y=x2+bx-^-c（b,c为常数）.（1）当b=2,c=—3时，求二次函数的最小值；（2）当c=5时，若在函数值y=l的情况下，只有一个口变量兀的值与其对应，求此时二次函数的解析式；（3）当c=b2时，若在口变量x的值满足bW«rWb+3的情况下，与其对应的函数值y的最小值为21,求此时二次函数的解析式.\n20.（木题13分）如图，在MBC中，ZACB=90°，点P到Z4CB两边的距离相等，RPA=PB.（1）先用尺规作出符合要求的点F（保留作图痕迹，不需要写作法），然后判断△加沪的形状，并说明理由；（2）设PA=m,PCm,试用加、〃的代数式表示AABC的周长和面积;（3）设CP与交于点Q,试探索当边AC>BC的长度变化时，£2+£2的值是ACBC否发生变化，若不变，试求出这个不变的值，若变化，试说明理山.（第20题图）BB（备用图）\n参考答案及评分标准一、选择题(每小题3分，共30分)1.A2.C3.B4.B5.D6.A7.D二、填空题(每小题4分，共24分)11.112.0+3)213.乙14.815.V3三、解答题.4_+4八(i~—417.解：(4)4-—atz2-4«+48.A9.A10.D16.-22a(a+2)+2)(。一4分a-a-28分当a=-\吋原工弋=_310分207AD丄尢轴于Q点，丄y轴于C点，A(-3,—).B(5,-4)_3R+b=—-18.解：根据题意得：32分5k+h=-4k=——解得：J34分348直线为：y=—x+—5分33当y=0时，x=2:.E(2,0)6分3・・・D(―3,0),C(0,—4)8分・•・DE=5,BC=5,CD=^OC2+OD2=a/42+32=59分乂JDE//CB10分・・・l川边形BCDE是菱形19.解：(1)当b=2,c=—3时，二次函数为：y=x2+2x-31分即)，=(兀+1)2—42分所以，当x=-l时，二次函数的最小值为-4.3分(2)当c=5时，二次函数为：y=x2+bx-^54分\n由题意得：方程x2+bx+5=l有两个相等的实数根5分\n所以△=/?2—16=0解得：仇=4,b2=—46分此时，二次函数的解析式为：y=兀‘+4兀+5或y=兀‘一4兀+57分(3)当c=h2吋，二次函数的解析式为：y=x2+hx+h2f图象的开口向上，对称轴为直线：x=--b.2①若—丄b(),在bJWb+3的情况下，y随着兀的增大而增大…8分2当x=b时，y=b2^-b2^b2m小，3/?2=21解得:b\=药，b2=-V7(不合舍去)…9分②若丄bb+3,即b<-2,在bWxWb+3的情况下，y随着兀的增大而减小…12分当x=b+3时，y=(b+3)2+〔@+3)+^2=3b2+9b+9的值最小3戸+%+9=21,解得：b}=1(不合舍去),b2=-4综上所述：b=4i戰b=—4此时，二次函数为：y=兀？+J7x+7或y=兀？一4兀+1620.解：(1)依题意，点戶既在Z4CB的平分线上，又在线段昇〃的垂直平分线上.如图1,作ZACB的平分线C7),作线段AB的垂直平分线MN,CD与MN的交点即为所求的P点。3分AABP是等腰直角三角形.理由：过点P分别作PE1AC.PF丄CB,垂足为F、尸如图2.VPC平分乙4CB,PE丄AC.PF丄CB,垂足为F、F,・・・PE=PF.XVPA=PB,・・・RtAAPE^RtABPF.4分・・・ZAPE=ZBPF.•:APEC=90°,ZPFC=90°,ZECF=90°,13分M：卜.J・・・ZEPF=90°,从而ZAPB=90°.又PA=PB:.AABP是等腰直角三角形.5分\n(2)如图2,在RtAPCE中，"EC=90。,PA—PB,PA=m.••AB—y[2m.由RtAAPERtABPF,APCE^APCF,可得AE=BF,CE=CF.:.CA+CB=CE+EA-}-CB=CE+CF=2CE.ePE耳2在RtAPCE+,APEC=90°,ZPCE=45°,PC=n,・°・CA+CB=2CE=yj~2n.6分所以△ABC的周长为：AB+BC+CA=4im+同.7分因为△ABC的面积=APAC的面积+APBC的面积—△P4B的面积=-•AC•PE-BC•PF•PA-PB=-(AC+BC)-PE--PA222222=—y[2n•丄匚〃一丄加？=—n2-—m2(n>m)9分222222、F).或S^Bc=^ACBC=|[(AC+BC)2-(AC2+BC2)]=|(/?(3)方法一：过点D分别作DW丄AC、DN丄BC,垂足为M、W如图3.•••DM=DN=:C£>-sin45°=-CD••2・・・10分由DN//AC得DNDB⑪.--11分ACAB111W//BC得DM_AD②12分BCAB①+②，得DNDMDB+AD1=ACBCAB即竺+竺ACBC・・・返(竺+竺2ACBC13分方法二:・・・DM-DNYDW匹CD.210分乂SmbCCD+SmcD12分13分S^BC•:S^CD+S遊D二丄ACDM+=BCDN=丄(AC+BC)•返CD11分4^24^・・・-(AC+BC)・乜CD=-ACBC.222・・・(AC+BC)CQ=q即CD+CD=^\CBCACBC方法三：过点£>作£>2丄BC,垂足为W如图4.\n在RtACDN中，ADCN=45°,DN=CN=—CD—2——10分由DN//AC得DNDB©:CN_AD(2>—11分ACABBCAB①+②，得DN+CN-DB+AD即DNJN_1—12分y—1•ACBCABACBC恥+竺)=1,2ACBC13分G方法四：过点3作BG//DC,交射线AC于点G如图5.・・・Z.G=ZACD=ZBCD=Z.CBG=45°,BG=42BC=V2CG.10分VBG//DC9・・・竺=竺.11分CDAC...41BCAC+BC(AC+BC)CQ二込丄分…CDAC，ACBC_°即竺+££=71.13分ACBCC图5方法五：过点A作CB的平行线，交射线CD于点K如图6.得CK=近AC,DK=CK-CD=42AC-CD——10分又竺=匹,即BCAK所以仅佞丝BCACCD_41AC-CD~BC~AC竺+竺W-ACBC12分•13分方法六：分别过点A、B分别作CD的平行线,交射线BC于点H,交射线AC于点G如图7.WAW=V2AC,BG=V2BC乂CDADCDBDBG~AB'AH~AB10分11分・・・竺+SAHBG12分即CD*CD42AC42BC器+器皿I?分