2016年初中数学能力达标练习03
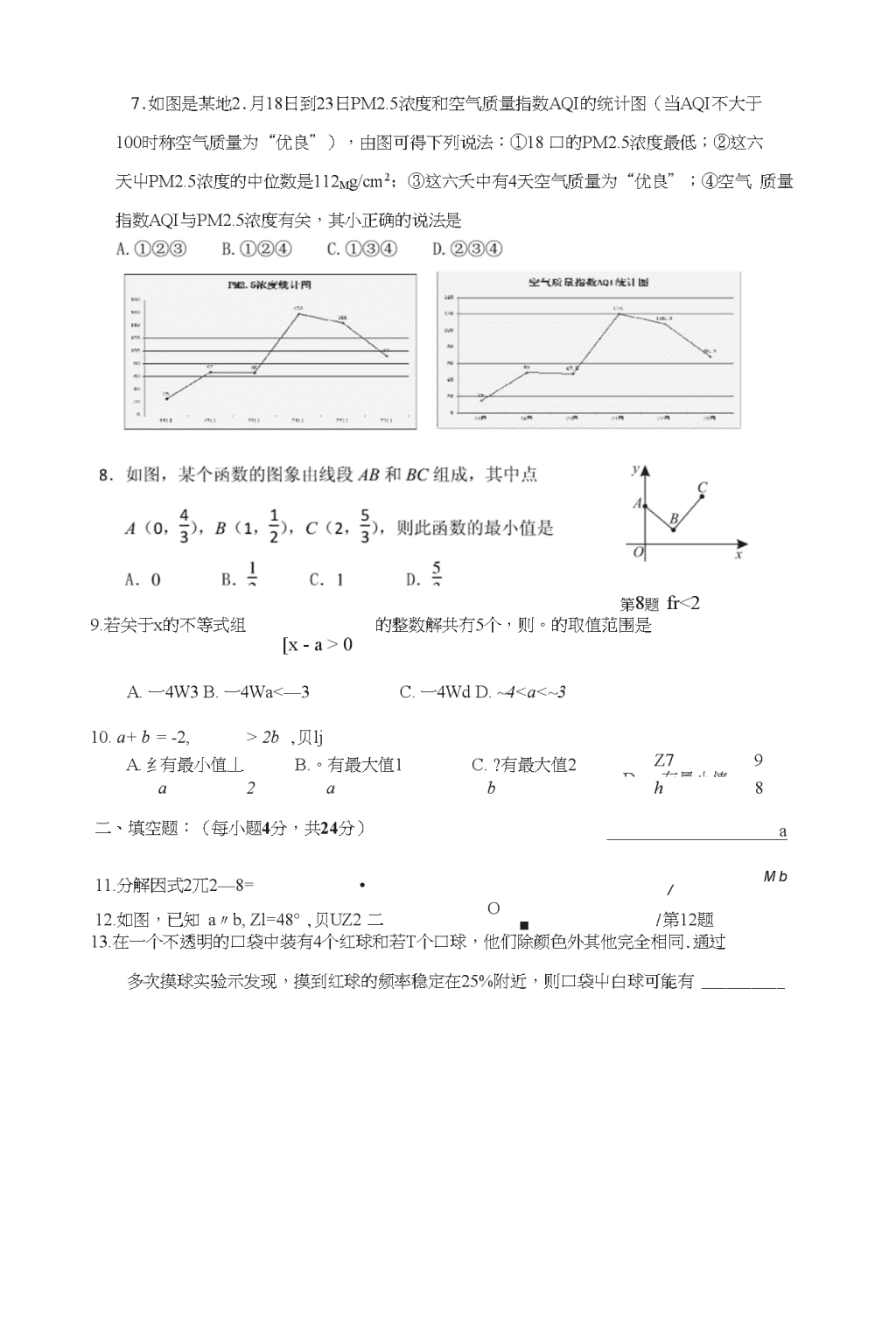
2016年初中数学能力达标练习(三)(满分:100分;考试时间:120分钟)选择题:(每小题3分,共30分)1.9的算术平方根是A.3B.一3C.±3D.812.如图是将正方体切去一个角后形成的几何体,则该几何体的左视图为ABC0/面第2题3.已知5ABC中,Z/二20。,ZB二乙C,那么三角形5ABC是A.锐角三角形B.直角三角形C.钝角三角形D.正三角形4.计算(6/2)3的结果是A.3/B.2/C.a5D.J5.已知一组数据:-2,5,2,-1,0,4,则这组数据的中位数是B.1-2A.6・如图,是用围棋了摆出的图案(围棋子的位置用有序数对表示,如A点在(5,1)),如果再摆放一黑一口两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则卜•列摆放正确的是A.黑(3,3),白(3,1)B.黑(3,1),白(3,3)C.黑(1,5),白(5,5)D•黑(3,2),白(3,3)\n7.如图是某地2.月18日到23日PM2.5浓度和空气质量指数AQI的统计图(当AQI不大于100时称空气质量为“优良”),由图可得下列说法:①18口的PM2.5浓度最低;②这六天屮PM2.5浓度的中位数是112Mg/cm2;③这六夭中有4天空气质量为“优良”;④空气质量指数AQI与PM2.5浓度有关,其小正确的说法是第8题fr<29.若关于x的不等式组的整数解共冇5个,则。的取值范围是[x-a>0A.一4W3B.一4Wa<—3C.一4WdD.~4
2b,贝ljA.纟有最小值丄B.。有最大值1C.?有最大值2Z79D.一有最小值-一a2abh8二、填空题:(每小题4分,共24分)a11.分解因式2兀2—8=•Mb/12.如图,已知a〃b,Zl=48°,贝UZ2二O■/第12题13.在一个不透明的口袋中装有4个红球和若T个口球,他们除颜色外其他完全相同.通过多次摸球实验示发现,摸到红球的频率稳定在25%附近,则口袋屮白球可能有\n个.14.如图,四边形ABCD是OO的内接四边形,若ZC=65°,则厶二°.\n15・一辆客车和一辆卡年同时从A地出发沿同一公路同方向行驶,客车的行驶速度是70km/h.卡车的行驶速度是60km/h,客车比卡车早lh到达3地.设客车经过x小时到达B地,依题意可列方程.(不必求解)16.如图①,己知肚是矩形纸片力BCD的对角线,/B=3,BC=4.现将矩形沿对角线/C剪开,再把沿着/D方向平移,得到图②中△4BC,当四边形A'ECF是菱形时,平移距离儿T的长是.三、解答题:(共46分)2317.(本题1()分)解方程:=+1,x-12%-2请川运算律和运算法则说明你求解的合理性.18.(本题12分)我们知道当人的视线与物体表面互相垂肓时的视觉效果最佳.如图是小明站在距离墙壁1.60米处观察装饰画时的示意图,此时小明的眼睹与装饰画底部力处于同一水平线上,视线恰好落在装饰画中心位置E处,且与/D垂直.己知装饰画的高度AD为0.66米.\n求:⑴装饰呵与墙壁的夹角ZCAD的度数(精确到1°⑵装饰画顶部到墙壁的距离DC(精确到0.01X)・16.(木题12分)已知。>一2,若当1WxW2时,函数夕=¥(占°)的最人值与最小值之差是1,求Q的值.17.(木题12分)定义:三边长和面积都是整数的三角形称为“整数三角形”数学学习小组的同学从32根等长的火柴棒(每根长度记为1个单位)中取出若干根,首尾依次相接组成三角形,进行探究活动.小亮用12根火柴棒,摆成如图所示的“整数三角形”;小颖分别用24根和30根火柴棒摆出岂角“整数三角形”;小辉受到小亮、小颖的启发,分别摆出三个不同的等腰“整数三角形”•⑴请你画出小颖和小辉摆出的“整数三角形”的示意图;⑵你能否也从屮取出若干根,按下列要求摆出“整数三角形”,如果能,请画出示意图;如果不能,请说明理由.①画出等边“整数三角形”;②摆出一个非特殊(既非直角三角形,也非等腰三角形),整数三角形”.\n参考答案及评分标准一、选择题:(每小题3分,共30分)I.A2.C3.A4.D5.B6.B7・C8・B9・A10・C二、填空题:(每小题4分,共24分)II.2(x+2)(x-2)12.13213.1214.11515.70x=60(x+1)16.2.5三、解答题:(共46分)9317.解方程:=+1x~12x—2解:方程两边都乘以2(x-1),得4=3+2(x~l)①1分去括号,得4=3+2x-2②—2分移项、合并同类项,得2x=3③3分方程两边都除以2,得3x=—④4分2检验:当X=—时,左边二4二右边23・・・兀=—是原方程的解.⑤……5分2第①步依据:等式基本性质2……6分第②步依据:去括号法则……7分第③步依据:等式基本性质1、合并同类项则……8分第④步依据:等式基本性质2……9分第⑤步依据:等式基本性质2……10分18.解:(1)・・・血)=0.66,:.AE=-CD=0.33.2分2在Rt/XABE中,・.丿AE0.33・smZABE=——=,AB1.6\n;・ZABES2。.・・・3分9:ZCAD+ZDAB=90°,ZABE+ZD4B=90°,:.ZCAD=ZABE=12°.・・・镜框与墙壁的夹角ACAD的度数约为12°.-6分(2)解法一:在RtACJD'P,cn9:s\nZCAD=—f・・・9分AD:.CD=AD・sinZC4D=0.66Xsinl2°^0.14.-12分解法二:•:ZCAD=ZABE,ZACD=ZAEB=90°,:.5ACDs/\BEA.9分.CD_AD.CD_0.66**033_TT*・・・C"0.14.・•・镜框顶部到墙壁的距离CD约是0.14米.……12分17.解1:(1)当一2VaV0时,在1WxW2范围内,随x的增大而增大,a•I2_df=1-/.a=—2不合题意,舍去.……6分(2)当a>0时,在1WxW2范围内丿随x的增大而减小,a••ci—空=1.ci—2..综上所述a=2.12分解2:(1)当dVO时,在1W/W2范围内夕随x的增人而增人,.a・・空—cz=1.<7=—2.\n又・・・-2VdV0:・a=—2不合题意,舍去.6分(2)当°>0吋,在范围内尹随x的增大而减小,\n•Ia=2.b=2.而血+2=4>0,符合题意,a=2.综上所述,a=2.12分17.解:⑴小颖摆出如图1所示的“幣数三也形”:6图1°小辉摆出如图2所示三个不同的等腰“整数三角形”:每摆出一个1分,共5分⑵①不能摆出等边“整数三角形”.理由如下:V3°设等边三角形的边长为g则等边三角形面积为—a2.因为,若边长a为整数,那么血积<3/一定非整数.4所以不存在等边“整数三角形”・•••9分②能摆出如图3所示一个非特殊“整数三角形”:……12分