- 2022-09-06 发布 |
- 37.5 KB |
- 11页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
100817初中阶段函数类基础练习题
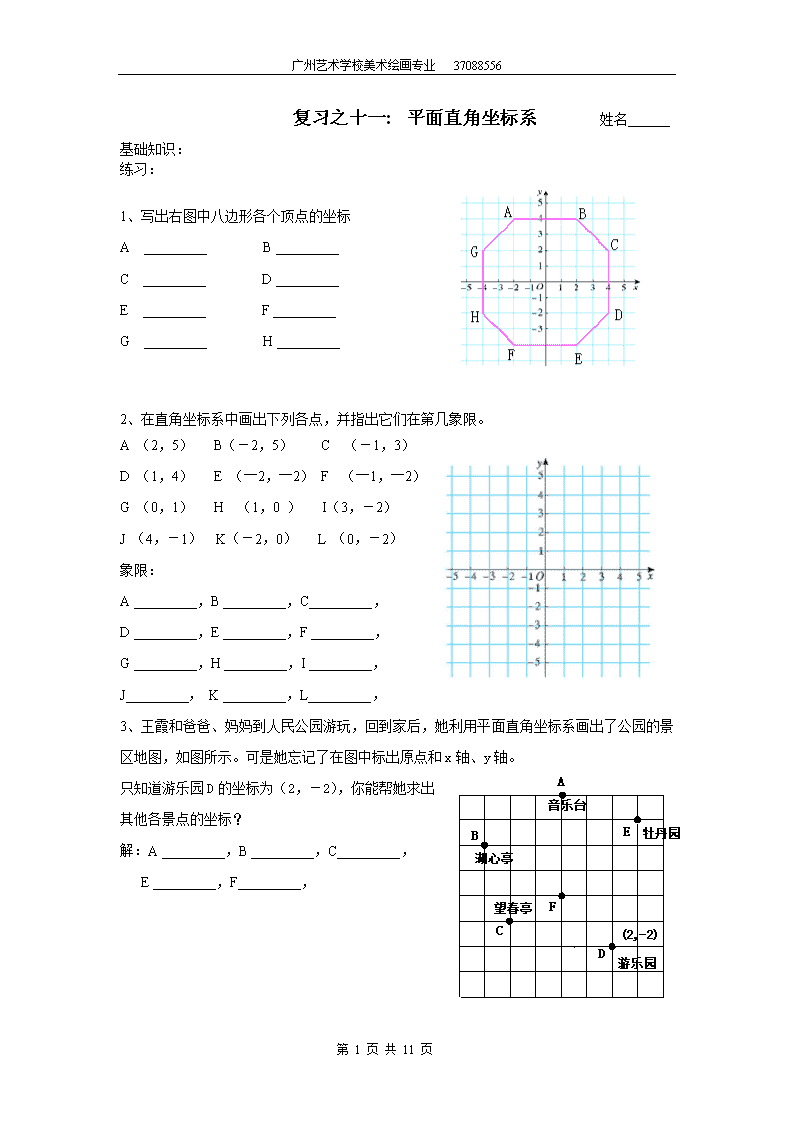
广州艺术学校美术绘画专业37088556复习之十一:平面直角坐标系姓名______基础知识:练习:1、写出右图中八边形各个顶点的坐标A_________B_________C_________D_________E_________F_________G_________H_________2、在直角坐标系中画出下列各点,并指出它们在第几象限。A(2,5)B(-2,5)C(-1,3)D(1,4)E(―2,―2)F(―1,―2)G(0,1)H(1,0)I(3,-2)J(4,-1)K(-2,0)L(0,-2)象限:A_________,B_________,C_________,D_________,E_________,F_________,G_________,H_________,I_________,J_________,K_________,L_________,3、王霞和爸爸、妈妈到人民公园游玩,回到家后,她利用平面直角坐标系画出了公园的景区地图,如图所示。可是她忘记了在图中标出原点和x轴、y轴。只知道游乐园D的坐标为(2,-2),你能帮她求出其他各景点的坐标?解:A_________,B_________,C_________,E_________,F_________,第11页共11页\n广州艺术学校美术绘画专业370885564、填空:(注意很多题目都要画图)(1)如果用(7,8)表示七年级八班,那么八年级七班可表示成.(2)已知点A(2,0)和点B(0,6)两点,且直线AB与坐标轴围成的三角形的面积等于_______;已知点A(a,0)和点B(0,5)两点,且直线AB与坐标轴围成的三角形的面积等于10,则a的值是________________(3)将点P(-3,y)向下平移3个单位,得到点Q(-3,0)则y=___________.(4)如果p(a+b,ab)在第二象限,那么点Q(a,-b)在第象限.(5)已知线段MN=4,MN∥y轴,若点M坐标为(-1,2),则N点坐标为.(6)点A(-3,5)在第_____象限,到x轴的距离为______,到y轴的距离为_______。(7)已知轴上点P到轴的距离是3,则点P坐标是_________。(8)将点P(-3,2)向下平移3个单位,向左平移2个单位后得到点Q(x,y),则xy=___________(9)如果点M(a,b)第二象限,那么点N(b,a)在第 象限。(10)已知点M与点N关于轴对称,则x+y=____。(11)已知点M在轴上,则点M的坐标为。(12)若点P到轴的距离为2,到轴的距离为3,则点P的坐标为_________5、如图,三角形AOB中,A、B两点的坐标分别是(2,4),(6,2)求三角形AOB的面积。第11页共11页\n广州艺术学校美术绘画专业37088556复习之十二:一次函数姓名______基础知识:一次函数和正比例函数:正比例:,()只有一个参数,所以只要一个点就能确定这个函数一次函数:,()有2个参数,所以要2个点来确定这个函数练习:1、画出下面几个函数的图像:(1)y=2x与y=2x+3;(2)y=2x+1与y=+1.观察(1)的两个图像,这两条直线的关系是________,观察(2)的两个图像,这两条直线的交点是_________,交点和b的值有关吗?_____有的话,根据规律,写出一条过交点的一次函数___________________________2、已知一个正比例函数经过点,求它的解析式。3、已知一个一次函数经过点和点,求它的解析式。4、已知是的一次函数,且当=8时,=15:当=-10时,=-3,求:⑴这个一次函数的解析式;⑵当=-2时,求的值;第11页共11页\n广州艺术学校美术绘画专业370885565、一个函数是经过原点的直线,并且这条直线经点(2,-3a)和点(1,a-5),求这个一次函数的解析式。6、已知函数(1)若函数图象经过原点,求的值(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围.7、在直角坐标系中有两条直线:L1:和L2:,它们的交点为P,第一条直线与轴交于点A,与轴交于点C,第二条直线与轴交于点B,与轴交于点D。(1)、求A、B两点的坐标;(2)求C、D两点的坐标;(3)求点P的坐标;(4)求△PAB的面积;(5)求△PCD的面积;(6)求四边形ABCD的面积;(提示:画简图来看)第11页共11页\n广州艺术学校美术绘画专业37088556复习之十三:反比例函数姓名______基础知识:1、右边是反比例函数的图像,左边一个为时的图像(1)当时,在图像的每一支上,随着的增大而__________(2)当时,在图像的每一支上,随着的增大而__________(3)点在反比例函数的图像上,则=_______,在图像的每一支上,随着的增大而__________(4)点在反比例函数的图像上,则=_______,在图像的每一支上,随着的增大而__________2、已知一次函数y=ax+b的图像与反比例函数的图像交于A(2,2),B(-1,m),求一次函数的解析式;3、(2009年广东省)如图所示,在平面直角坐标系中,一次函数的图象与反比例函数的图象在第一象限相交于点.过点分别作轴、轴的垂线,垂足为点、.如果四边形是正方形,求一次函数的关系式.ACOBx第11页共11页\n广州艺术学校美术绘画专业370885564、直线与反比例函数(<0)的图象相交于点A、点B,与x轴交于点C,其中点A的坐标为(-2,4),点B的横坐标为-4.(1)试确定反比例函数的关系式;(2)求△AOC的面积.5、如图,已知,是一次函数的图像和反比例函数的图像的两个交点.(1)求反比例函数和一次函数的解析式;(2)求直线与轴的交点的坐标及三角形的面积.(3)当为何值时,一次函数的值小于反比例函数的值?6、为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量(mg)与燃烧时间(分钟)成正比例;燃烧后,与成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.据以上信息解答下列问题:(1)求药物燃烧时与的函数关系式.第11页共11页\n广州艺术学校美术绘画专业37088556(2)求药物燃烧后与的函数关系式.(3)当每立方米空气中含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,经多长时间学生才可以回教室?复习之十四:二次函数姓名______基础知识:二次函数:一般式:有3个点,一般需要三个未知数来确定顶点式:其中为顶点坐标,为对称轴图像:为抛物线(主要是确定:开口方向和顶点位置)如右图为对应的两个函数的图像如果能把一个函数画出顶点式,那么它的对称轴、顶点。图像都很容易就确定下来了。把函数的解析式写成顶点式的方法有2种:配方法和公式法其中公式法:对称轴,最大(最小值):1、画出下面两个函数的图像:(1)(2)第11页共11页\n广州艺术学校美术绘画专业370885562、配方法求二次函数的最大(小)值,和对称轴例:(1)(2)解:对称轴:,最小值:(3)(4)3、用公式法求二次函数的最大(小)值,和对称轴(1)(2)4、求二次函数的解析式(1)已知二次函数的解析式为,它的图像经过点,求出它的解析式;(2)已知二次函数的解析式为,它的图像经过点和点,求出它的解析式;(3)已知二次函数的解析式为,它的图像经过点和点和点,求出它的解析式;第11页共11页\n广州艺术学校美术绘画专业37088556(4)已知二次函数的顶点式为,它的图像的最高点为,而且经过点,求它的解析式。5、二次函数与一元二次方程:(1)一元二次方程的韦达定理:设是方程的两根,那么有,(2)二次函数与轴的交点,即,得到所以得到2个交点为,它们的距离:根据完全平方公式可以得到:即:(套用韦达定理)(3)由于与轴相交得到,所以可以根据判别式判断出二次函数与轴的交点个数。:1个交点:2个交点:没有交点练习:1、填空:(1)已知一元二次方程的两根分别为1和2,那么______,______;已知一元二次方程的两根分别为和,那么____,___(2)已知抛物线与轴的两根交点为A和B,那么线段AB的长度为________。(3)已知抛物线,那么这个抛物线与轴有几个交点?_________已知抛物线,那么这个抛物线与轴有几个交点?_________已知抛物线,那么这个抛物线与轴有几个交点?_________(4)已知抛物线,则它与轴的交点为__________________已知抛物线,则它与轴的交点为__________________第11页共11页\n广州艺术学校美术绘画专业370885562、已知二次函数,它与轴相交于点和点(1)求,(2)求,3、已知抛物线y=x2+x-.(1)用配方法求出它的顶点坐标和对称轴;(2)若抛物线与x轴的两个交点为A、B,求线段AB的长.yxBACO4、如图:二次函数()的图象与轴交于两点,与轴交于点,的面积为.(1)求该二次函数的关系式;5、如图,已知抛物线与交于A(-1,0)、E(3,0)两点,与轴交于点B(0,3)。(1)求抛物线的解析式;(2)设抛物线顶点为D,求四边形AEDB的面积;第11页共11页\n广州艺术学校美术绘画专业37088556第11页共11页查看更多