初中数学点线面专项练习

初中数学点线面专项练习

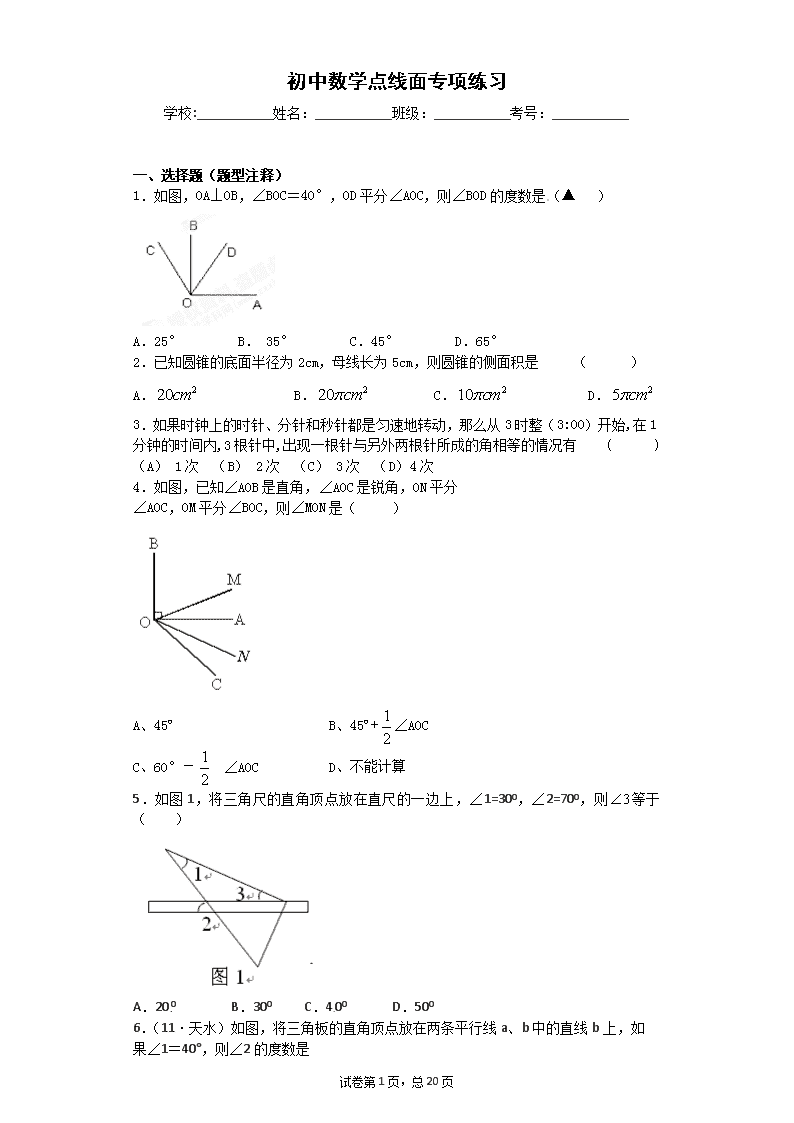
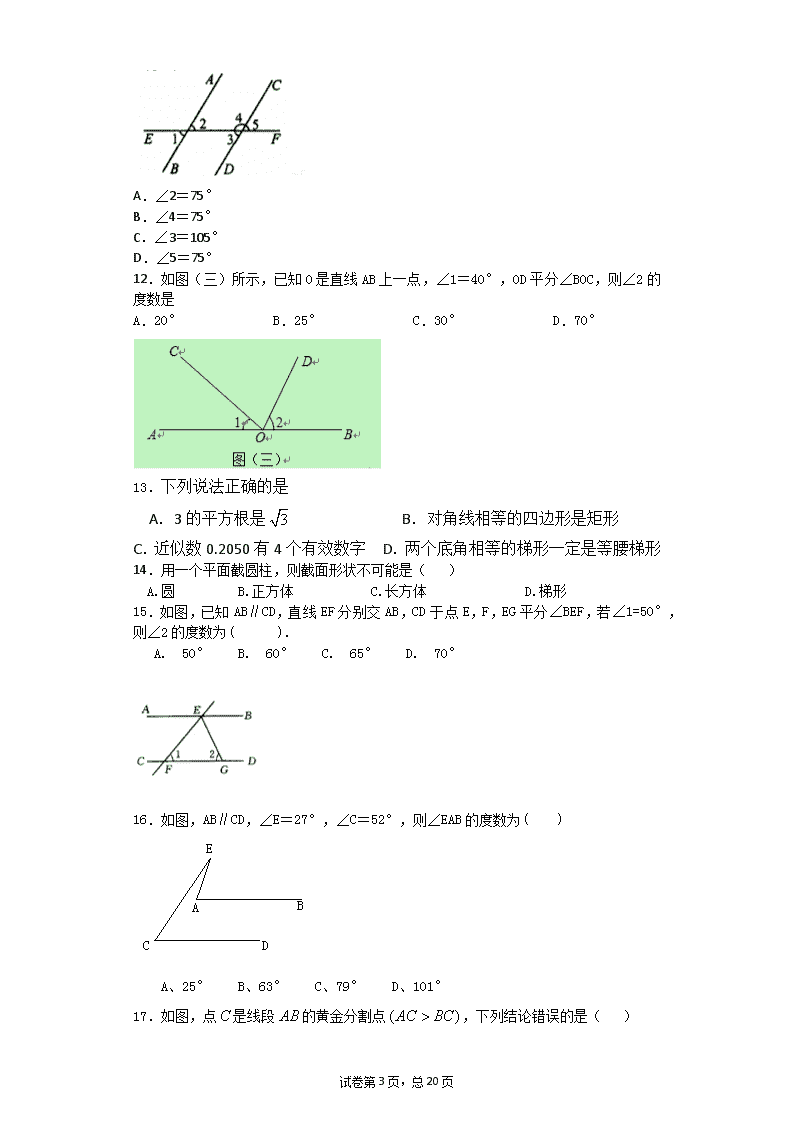
初中数学点线面专项练习学校:___________姓名：___________班级：___________考号：___________一、选择题（题型注释）1．如图，OA⊥OB，∠BOC＝40°，OD平分∠AOC，则∠BOD的度数是（▲）A．25°　　B．35°　　C．45°　　　D．65°2．已知圆锥的底面半径为2cm，母线长为5cm，则圆锥的侧面积是（）A．B．C．D．3．如果时钟上的时针、分针和秒针都是匀速地转动，那么从3时整（3:00）开始,在1分钟的时间内,3根针中,出现一根针与另外两根针所成的角相等的情况有()（A）1次（B）2次（C）3次（D）4次4．如图，已知∠AOB是直角，∠AOC是锐角，ON平分∠AOC，OM平分∠BOC，则∠MON是（）A、45ºB、45º+∠AOCC、60°－∠AOCD、不能计算5．如图1，将三角尺的直角顶点放在直尺的一边上，∠1=300，∠2=700，则等于（）A．200B．300C．400D．5006．（11·天水）如图，将三角板的直角顶点放在两条平行线a、b中的直线b上，如果∠1＝40°，则∠2的度数是试卷第19页，总20页\nA．30°B．45°C．40°D．50°7．（2011广西崇左，13，3分）如图所示BC//DE，∠1=108°，∠AED=75°，则∠A的大小是（）A．60°B．33°C．30°D．23°8．（2011•德州）如图，直线l1∥l2，∠1=40°，∠2=75°，则∠3等于（　　）A、55°B、60°C、65°D、70°9．如图1，∠1＋∠2等于A．60°B．90°C．110°D．180°10．下面四个图形中，∠1=∠2一定成立的是（）．11．如图所示，两条直线AB、CD被第二条直线EF所截，∠1＝75°，则下列条件，能使AB∥CD的是（）试卷第19页，总20页\nA．∠2＝75°B．∠4＝75°C．∠3＝105°D．∠5＝75°12．如图（三）所示，已知O是直线AB上一点，∠1＝40°，OD平分∠BOC，则∠2的度数是A．20°B．25°C．30°D．70°13．下列说法正确的是A．3的平方根是B．对角线相等的四边形是矩形C．近似数0.2050有4个有效数字D．两个底角相等的梯形一定是等腰梯形14．用一个平面截圆柱，则截面形状不可能是（）A.圆B.正方体C.长方体D.梯形15．如图，已知AB∥CD，直线EF分别交AB，CD于点E，F，EG平分∠BEF，若∠1=5O°，则∠2的度数为(　)．　A.　50°B.　6O°C.　65°D.　7O°16．如图，AB∥CD，∠E＝27°，∠C＝52°，则∠EAB的度数为()ECABDA、25°B、63°C、79°D、101°17．如图，点是线段的黄金分割点，下列结论错误的是（）试卷第19页，总20页\nA.B.C.D.18．如右图所示，从A地到达B地，最短的路线是（）．（A）A→C→E→B（B）A→F→E→B（C）A→D→E→B（D）A→C→G→E→B19．下列说法中：①过两点有且只有一条直线，②两点之间线段最短，③到线段两个端点距离相等的点叫做线段的中点，④线段的中点到线段的两个端点的距离相等。其中正确的有（）A、1个B、2个C、3个D、4个20．如图，AB、CD相交于点O，EOAB于O，则图中1与2的关系是（）（无图）A、对顶角，B、互补的两角，C、互余的两角，D、一对相等的角21．下列不正确的几何语句是（）直线AB与直线BA是同一条直线射线OA与射线OB是同一条射线射线OA与射线AB是同一条射线D．线段AB与线段BA是同一条线段22．如果正五边形绕着它的中心旋转角后与它本身重合，那么角的大小可以是（）．36°；．45°；．72°；．90°．23．如图，已知线段AB=8cm，点C是AB上任一点，点M、N分别是AC和CB的中点，则MN的长度为A．5cmB．4cmC．3cmD．2cm24．下列叙述正确的是（）（A）画直线AB=10厘米（B）若AB=6，BC=2，那么AC=8或4（C）河道改直可以缩短航程，是因为“经过两点有一条直线，并且只有一条直线”。（D）在直线AB上任取4点，以这4个点为端点的线段共有6条试卷第19页，总20页\n25．图中是形状、大小都相同的两个长方形，第一个长方形的阴影面积为m，第二个长方形的阴影面积为n，则m与n关系为（）A.m＞nB.m＝nC.m＜nD.不确定26．已知：如图，BD平分∠ABC，点E在BC上，EF∥AB．若∠CEF=100°，则∠ABD的度数为（　　）　　A．60°　　B．50°　　C．40°　　D．30°27．如图,直线，垂足为点，平分，则的度数为　　　（　　）　　　　Ａ．　　　Ｂ．　　　　　　Ｃ．　　　　　Ｄ．28．如图，平分，，图中相等的角共有（）Ａ．3对　　　　Ｂ．4对　　　　　　Ｃ．5对　　　　　Ｄ．6对29．点为直线外一点，点、、为直线上三点，，，，则点到直线的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）　　　　Ａ．　　　　Ｂ．小于　　　　Ｃ．不大于　　　　Ｄ．试卷第19页，总20页\n第II卷（非选择题）请点击修改第II卷的文字说明二、填空题（题型注释）30．(15届江苏初一1试)一条一条直街上有5栋楼，按从左至右顺序编号为1、2、3、4、5，第k号楼恰好有k（k=1、2、3、4、5）个A厂的职工，相邻两楼之间的距离为50米.A厂打算在直街上建一车站，为使这5栋楼所有A厂职工去车站所走的路程之和最小，车站应建在距1号楼米处.31．下面是六个推断：①因为平角的两条边在一条直线上，所以直线是一个平角；②因为周角的两条边在一条射线上，所以射线是一个周角；③因为扇形是圆的一部分，所以圆周的一部分是扇形；④因为平行的线段没有交点，所以不相交的两条线段平行；⑤因为正方形的边长都相等，所以边长相等的四边形是正方形；⑥因为等腰三角形有两个内角相等，所以有两个内角相等的三角形是等腰三角形；其中正确的结论有,个，其序号是；32．如图，∠C=45°，∠B=45°+2，∠C=45°+3，AE平分∠BAD，则∠CAE=；ABCDE33．34．下列命题①不相交的直线是平行线；②同位角相等；③矩形的对角线相等且互相平分；④平行四边形既是中心对称图形又是轴对称图形；⑤同圆中同弦所对的圆周角相等。其中错误的序号是。35．（2011山东济南，19，3分）如图，直线l与直线a、b分别交与点A、B，a∥b，若∠1=70°，则∠2=　　°．试卷第19页，总20页\n36．（11·佛山）已知线段AB＝6，若C为AB中点，则AC＝；37．（2011广西崇左，5，2分）在修建崇钦高速公路时，有时需要将弯曲的道路改直，依据是___________.38．如图2，点B、C、D在同一条直线上，CE//AB，∠ACB＝90°，如果∠ECD＝36°，那么∠A＝_________．39．（2011•湛江）已知∠1=30°，则∠1的补角的度数为____________度40．如图，直线AB、CD相交于点O，∠EOC=70°，OA平分∠EOC，则∠BOD=.41．（2011•衢州）如图，直尺一边AB与量角器的零刻度线CD平行，若量角器的一条刻度线OF的读数为70°，OF与AB交于点E，那么∠AEF=___________．42．如图（五）所示，AB∥CD，MN分别交AB、CD于点F、E．已知∠1＝35°，∠2＝．MBFACDEN12图（五）43．正多边形的每个内角等于，则这个正多边形的边数为______________条．44．图形是由________,__________,____________构成的.45．如图，在中，边的垂直平分线分别交、于点、，已知，，则的周长为．试卷第19页，总20页\n46．一个承重架的结构如图所示，如果，那么度．47．在中，，于点，cm，则cm.48．已知是2和6的比例中项，则．49．已知α，β都是钝角，甲、乙、丙、丁四人计算(α+β)的结果依次为28º，48º，88º，60º，其中只有一个是正确的，那么算的正确的是。50．如图，O是直线AB上的一点，OD平分∠AOC，OE平分∠BOC,则∠DOE=______.51．已知：P是线段AB的中点，PA=3cm,则AB=______cm.52．度分秒53．如图，∠AOC=∠BOD=90°，且∠AOB=162°，则∠COD=度。54．正十五边形的内角等于度．55．如图：PC//AB，QC//AB，则点P、C、Q在一条直线上。理由是：.56．如下图，已知AB=20cm，C是AB的中点，D为BC上一点，E为BD的中点，BE=3cm，则CD等于____cm．57．如图，，，.则的度数为.试卷第19页，总20页\n58．如果一个正多边形的一个外角是60°，那么这个正多边形的边数是．59．已知一个多边形的内角和是外角和的，则这个多边形的边数是.60．如图，在△ABC中，BD是∠ABC的角平分线，已知∠ABC=80°，则∠DBC=．61．如图，△ABC中，∠A=96°，延长BC到D,∠ABC与∠ACD的平分线相交于A1点，则∠A1的大小是,∠A1BC与∠A1CD的平分线相交于A2点，依次类推，∠A2012BC与∠A2012CD的平分线相交于∠A2012的大小是BACDA1A2三、计算题（题型注释）四、解答题（题型注释）62．如图，线段AB的端点在边长为1的小正方形网格的格点上，现将线段AB绕点A按逆时针方向旋转90°得到线段AC．⑴请你在所给的网格中画出线段AC及点B经过的路径；⑵若将此网格放在一平面直角坐标系中，已知点A的坐标为(1，3)，点B的坐标为(-2，-1)，则点C的坐标为；⑶线段AB在旋转到线段AC的过程中，线段AB扫过的区域的面积为；⑷若有一张与⑶中所说的区域形状相同的纸片，将它围成一个几何体的侧面，则该几何体底面圆的半径长为.63．（10分，当总分已达95分时，此题得分不计入总分；当总分不到95分时，计入总分．但计入总分后，总分不得超过95分.）试卷第19页，总20页\n　　如图为3×3的正方形，求∠1+∠2+∠3+…+∠7+∠8+∠9的和．64．在同一平面内有n条直线，任何两条不平行，任何三条不共点。当n=1时，如图⑴，一条直线将一个平面分成两个部分；当n=2时，如图⑵，两条直线将一个平面分成四个部分；则：当n=3时，三条直线将一个平面分成部分；当n=4时，四条直线将一个平面分成部分；若n条直线将一个平面分成个部分，n+1条直线将一个平面分成个部分。试探索、、n之间的关系。65．已知，AB∥ED，α=∠A+∠E，β=∠B+∠C+∠D，证明：β=2α.66．已知，如图，AB∥ED，点F、点C在AD上，AB=DE,AF=DC.求证：BC=EF.67．如图，要在一块形状为直角三角形（∠C为直角）的铁皮上裁出一个半圆形的铁皮，需先在这块铁皮上画出一个半圆，使它的圆心在线段AC上，且与AB、BC都相切.请你用直尺和圆规画出来（要求用尺规作图，保留作图痕迹，不要求写作法）．68．如图，给出下列论断:试卷第19页，总20页\n(1)AB∥DC；(2)AD∥BC；(3)∠A+∠B=180°；(4)∠B+∠C=180°，以其中一个作为题设，一个作为结论，写出一个真命题.想一想，若连接BD，你能自已写出一个真命题吗?试写出—个真命题并写出推理过程.69．认真阅读下面关于三角形内外角平分线所夹的探究片段，完成所提出的问题.探究1：如图1，在中，是与的平分线和的交点，通过分析发现,理由如下:∵和分别是和的角平分线(1)探究2：如图2中,是与外角的平分线和的交点，试分析与有怎样的关系？请说明理由.(2)探究3：如图3中，是外角与外角的平分线和的交点，则与有怎样的关系？（直接写出结论）(3)拓展:如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？（直接写出结论）70．如图，如果平分，，相等吗？请说明理由．71．如图1，射线OC、OD在∠AOB的内部，且∠AOB=150°，∠COD=30°，射线OM、ON分别平分∠AOD、∠BOC，（1）求∠MON的大小，并说明理由；试卷第19页，总20页\n（2）如图2，若∠AOC=15°，将∠COD绕点O以每秒x°的速度逆时针旋转10秒钟，此时∠AOM︰∠BON=7︰11，如图3所示，求x的值．72．根据题意，将证明过程的理由填写在后面的括号内。已知：如图,AB∥CD，AD∥BC.求证：∠A＝∠C.证明：∵AB∥CD（_________）∴∠B+∠C=180°（）∵AD∥BC（已知）∴∠A+∠B=180°（）∴∠A＝∠C.()73．如图，点C在线段AB上，线段AC=8cm，BC=4cm，点M、N分别是AC、BC的中点，求：线段MN的长度。根据（1）的计算过程和结果，设AC+BC=，其它条件不变，你能猜测出MN的长度吗？请证明你的猜测。74．如图，∠AOB=110°，∠COD=70°，OA平分∠EOC，OB平分∠DOF，求∠EOF。75．已知线段a、b，请画一条线段等于2a-b。（不写画法，保留作图痕迹）76．A,B,C,D四点如图所示,读下列语句,按要求作出图形(不写画法):(1)连接AD,并延长线段DA;(2)连接BC,并反向延长线段BC;(3)连接AC,BD,它们相交于O;试卷第19页，总20页\n(4)DA延长线与BC反向延长线交于点P.77．已知∠AOB=80°，过O作射线OC（不同于OA、OB），满足∠AOC=∠BOC，求∠AOC的大小。（注：本题中所说的角都是指小于平角的角）78．一个角的余角比它的补角的还少40º，求这个角.79．如图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，OE⊥OD．ABCOED（1）求∠BOD的度数；（2）请通过计算说明OE是否平分∠BOC。80．如图所示已知，，OM平分，ON平分；；如图∠AOB＝900，将OC绕O点向下旋转，使∠BOC＝，仍然分别作∠AOC，∠BOC的平分线OM，ON，能否求出∠MON的度数，若能，求出其值，若不能，试说明理由．试卷第19页，总20页\n(3)，，仍然分别作∠AOC，∠BOC的平分线OM，ON，能否求出∠MON的度数，若能，求的度数；并从你的求解中看出什么什么规律吗？81．直线AB、CD被直线所截，EF分别交于M，N,平分．（1）如图1，若，求的度数．（2）如图2，若，求的度数．82．如图，点O在直线AD上，∠EOC=90°，∠DOB=90°，若，求∠AOC的度数OAＤＢＣＥ83．如图，点P是的边OB上的一点。试卷第19页，总20页\n⑴过点P画OA的垂线，垂足为H；⑵过点P画OB的垂线，交OA于点C；⑶线段PH的长度是点P到　　的距离；_____　　是点C到直线OB的距离。因为直线外一点到直线上各点连接的所有线段中，垂线段最短，所以线段PC、PH、OC这三条线段大小关系：是　　　　　　　　。（用“<”号连接）84．如图，在△ABC中，CD与C，分别是△ABC的内角、外角平分线，DF//BC交AC于点E．试说明(1)△DCF为直角三角形；(2)DE=EF．85．作图题（要求：画出图形，保留作图痕迹，并简要说明画法，不要求证明）.已知∠AOB及其内部一点P.（1）如图1，若点P在∠AOB的角平分线上，请你在图1中过点P作直线，分别交OA、OB于点C、D，使△OCD为等腰三角形，且CD是底边；（2）若点P不在∠AOB的角平分线上（如图2），请你在图2中过点P作直线，分别交OA、OB于点C、D，使△OCD为等腰三角形，且CD是底边.86．已知：直线AB与直线CD相交于点O，∠BOC=，试卷第19页，总20页\n（1）如图1，若EO⊥AB，求∠DOE的度数；（2）如图2，若EO平分∠AOC，求∠DOE的度数．87．已知，为上一点．（1）过点画一条直线，使∥；（2）过点画一条直线，使⊥交于点；（3）若，则°．88．如图，点C在线段AB上，AC=16cm，CB=12cm，点M、N分别是AC、BC的中点。（1）求线段MN的长；（2）若C为线段AB上任一点，满足AC+CB=acm，其它条件不变，你能猜想MN的长度吗？并说明理由。（3）若C在线段AB的延长线上，且满足ACBC=bcm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，不要说明理由。89．作图题：（1）作四边形ABCD关于直线a的对称图形。（2）已知∠AOB，试在∠AOB内确定一点P，使P到OA、OB的距离相等，并且到M、N两点的距离也相等。（要求：保留作图痕迹，不写作法）。90．如下图，O为直线AB上一点，∠AOC=50°，OD平分∠AOC，∠DOE=90°（1）求出∠AOD的补角的度数；试卷第19页，总20页\n（2）试判断OE是否平分∠BOC，并说明理由。91．实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等。（2+2+2+2+2+4分，共14分）(1)如图,一束光线m射到平面镜a上,被a反射到平面镜b上,又被b反射.若被b反射出的光线n与光线m平行,且∠1=38°,则∠2=°,∠3=°。(2)在(1)中,若∠1=55°,则∠3=°;若∠1=40°,则∠3=°。(3)由(1)、(2),请你猜想:当两平面镜a、b的夹角∠3=___°时,可以使任何射到平面镜a上的光线m,经过平面镜a、b的两次反射后,入射光线m与反射光线n平行.你能说明理由吗?92．如图：两个同心圆的半径所截得的弧长AB=6cm，CD=10cm，且AC=12cm。（1）求两圆的半径长。（2）阴影部分的面积是多少？93．如图，已知点在直线上，点在直线上，若．，则与相等吗？为什么？94．如图，，，．问吗？为什么？95．如图所示，A、B两村在一条公路的同一侧，现在要在路边建一垃圾回收站，（1）若要使垃圾回收站M到两村的距离之和最短，回收站M应选在哪个位置最合适；（2）若要使垃圾回收站M到两村的距离相等，回收站M应选在哪个位置最合适。（在图中作出M的位置，并保留作图痕迹）试卷第19页，总20页\n96．在下列解题过程的空白处填上适当的内容（推理的理由或数学表达式）如图，已知AB∥CD，BE、CF分别平分∠ABC和∠DCB，求证：BE∥CF．ABCDFE证明：∵AB∥CD，（已知）∴∠_____=∠_____．（）∵，（已知）∴∠EBC=∠ABC．（角的平分线定义）同理，∠FCB=．∴∠EBC=∠FCB．（等式性质）∴BE∥CF．（）97．在△ABC中，D为BC的中点，E为AC上任一点，BE交AD于O，某学生在研究这一问题时，发现了如下事实：　　（1）当==时，有=；　　（2）当==时，有=；　　（3）当==时，有=；　　1）当=时，按照上述的结论，请你猜想用n表示AO/AD的一般性结论（n为正整数）；　　2）若＝，且AD=18,求AO.试卷第19页，总20页\n98．如图，AB为⊙O的直径，弦CD⊥AB，垂足为点E，CF⊥AF，且CF=CE．（1）求证：CF是⊙O的切线；（2）若sin∠BAC=，求的值．99．已知：点A、B分别在直角坐标系的x、y轴的正半轴上，O是坐标原点，点C在射线AO上，点D在线段OB上，直线AD与线段BC相交于点P，设=a，=b，=k。（1）如图1，当a=，b=1时，请求出k的值；（2）当a=，b=1时(如图2)，请求出k的值；当a=，b=时，k=▲；（3）根据以上探索研究，请你解决以下问题：①请直接写出用含a，b代数式表示k=▲；②若点A(8,0)，点B（0，6），C（－2，0），直线AD为：y=－x+4，则k=▲。100．（1）在图①正方形网格中，已知∠AOB及点E、F，现要求只用直尺，分别以E、F为顶点.画∠CEH、∠PFK，使∠CEH与∠AOB互余，且CE与OB互相垂直；使∠PFK与∠AOB互补，且FP∥OA，FK∥OB.（2）在图②中，已知∠AOB，点E在OB上，请先用量角器画射线EC，使EC⊥EB于E，交OA于C，再用尺规作射线EH，使∠CEH与∠AOB互余，且EH∥OA.（保留痕迹，不写作或画法，不说明理由）.试卷第19页，总20页\n试卷第19页，总20页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。参考答案1．A【解析】略2．C【解析】圆锥的侧面积=，故选C3．D【解析】略4．A【解析】略5．C【解析】略6．D【解析】略7．B【解析】略8．C【解析】略9．B【解析】略10．B【解析】略11．D【解析】略12．D【解析】∵∠1+∠COB=∠2=∠COD∴∠2=13．C【解析】略14．D【解析】解：用平行于底的平面截，截面为圆，用垂直于底的平面截，截面为长方形或正方形，但无法截到梯形，故选D。15．C【解析】因为AB∥CD，所以又因为EG平分∠BEF，所以°，因为AB∥CD，所以∠2=°。故选C16．C【解析】延长EA交CD于F．答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。根据三角形的一个外角等于和它不相邻的两个内角和，得∠EFC=∠C+∠E=79°．再根据平行线的性质：两条直线平行，同位角相等，得：∠EAB=79°．故选C．17．B【解析】解：∵AC＞BC，∴AC是较长的线段，根据黄金分割的定义可知：，故A正确，不符合题意；，故B错误，，故C正确，不符合题意；，故D正确，不符合题意．故选B．18．B【解析】两点之间线段最短，故从A地到达B地，最短的路线是A→F→E→B，故选B19．C【解析】分析以上语句，①②④正确，到线段两个端点距离相等的点在线段的垂直平分线上，而不一定是线段的中点，故③错误。故选C20．C【解析】，因为与2互余，所以1与2互余。故选C21．C【解析】解：A正确，因为直线向两方无限延伸；B正确，射线的端点和方向都相同；C错误，因为射线的端点不相同；D正确．故选C．22．C【解析】正五边形绕着它的中心旋转后与它本身重合，最小的旋转角度数是360/5=72度．故选C．23．B【解析】解：∵M是AC的中点，N是BC的中点，∴MC=AM=AC，CN=BN=BC，∴MN=MC+CN=AC+BC=（AC+BC）=AB=4cm．答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。故选B．【答案】D【解析】A、直线没长度，故本选项错误；B、若AB=6，BC=2，不能确定C在不在直线AB上，那么AC=不一定为8或4，故本选项错误；C、河道改直可以缩短航程，是因为“两点之间线段最短”，故本选项错误；D、在直线AB上任取4点，以这4点为端点的线段共有6条，故本选项正确．故选D．25．B【解析】解：由图形可得：第一个矩形中阴影部分的面积m=；第二个矩形中阴影部分的面积n=；∴m=n．故选B．26．B【解析】解：∵EF∥AB，∠CEF=100°，∴∠ABC=∠CEF=100°，∵BD平分∠ABC，∴∠ABD=∠ABC=×100°=50°．故选B．27．C【解析】∵EO⊥CD，∴∠EOD=90°，∵AB平分∠EOD，∴∠AOD=45°，∴∠BOD=180°-45°=135°，故选C．28．C【解析】∵DE∥BC，∴∠DEB=∠EBC，∠ADE=∠ABC，∠AED=∠ACB，又∵BE平分∠ABC，∴∠ABE=∠EBC．即∠ABE=DEB．所以图中相等的角共有5对．故选C．29．C【解析】∵根据点到直线的距离为点到直线的垂线段（垂线段最短），2＜4＜5，∴点P到直线l的距离小于等于2，即不大于2，故选C．30．150【解析】略31．1，⑥【解析】略32．126°【解析】略33．45°【解析】略34．①②④⑤【解析】略35．110【解析】答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。∵a∥b，∠1=70°，∴∠3=∠1=70°，∵∠2+∠3=180°，∴∠2=110°．故答案为：110．36．3【解析】略37．两点之间线段最短【解析】略38．54【解析】略39．150【解析】∵∠1=30°，∴∠1的补角的度数为=180°﹣30°=150°．故答案为：150．40．35°【解析】略41．70°【解析】略42．35°【解析】两直线平行，同位角相等。43．12【解析】多边形内角和为180º（n-2）,则每个内角为180º（n-2）／n＝,n=12,所以应填12.44．点、线、面【解析】解：图形是由点、线、面构成的。45．18【解析】解：是边的垂直平分线，，46．65【解析】解：根据“三角形的外角等于与它不相邻的两个内角的和”得，则47．3答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。【解析】解：，，根据“三线合一”可得48．【解析】解：由题意得，，，49．乙【解析】解：∵α，β都是钝角，∴90°＜α＜180°，90°＜β＜180°，∴180°＜α+β＜360°，∴30°＜（α+β）＜60°，∴28°，48°，88°，60°四个结果中，只有48°是正确的．所以算的正确的是乙．50．900【解析】因为角AOB是平角，OD平分∠AOC，OE平分∠BOC,，所以∠DOE=180÷2=90°。51．6【解析】AB=2PA=6cm52．362512【解析】0.42°=25分12秒，所以36度25分12秒53．18【解析】解：∵∠BOC=∠AOB-∠AOC=162°-90°=72°，∴∠COD=∠BOD-∠BOC=90°-72°=18°．54．156【解析】先利用外角和360°除以边数求出每一个外角的度数，然后根据外角与内角是平角列式进行计算即360°÷15=24°，180°-24°=156°，55．过直线外一点有且只有一条直线和已知直线平行【解析】解：∵PC∥AB，QC∥AB，∵PC和CQ都过点C，∴P、C、Q在一条直线上（过直线外一点有且只有一条直线平和已知直线平行）。56．4【解析】解：∵AB=20cm，C是AB的中点，∴AC=10cm，又∵E为BD的中点，BE=3cm，∴BD=2BE=6cm，∴CD=AB-AC-BD=20-10-6=4cm．57．100°【解析】因为，所以°，又因为，所以°，所以=100°58．6【解析】设所求正n边形边数为n，则60°•n=360°，答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。解得n=6．故正多边形的边数是6．59．5【解析】根据内角和与外角和之间的关系列出有关边数n的方程求解即可：设该多边形的边数为n则（n﹣2）×180=×360。解得：n=5。60．40°【解析】解：∵BD是∠ABC的角平分线，∠ABC=80°，∴∠DBC=∠ABD=∠ABC=×80°=40°。61．48°,【解析】解：∵A1B平分∠ABC，A1C平分∠ACD，∴∠A1BC=∠ABC，∠A1CA=∠ACD，∵∠A1CD=∠A1+∠A1BC，即∠ACD=∠A1+∠ABC，∴∠A1=（∠ACD-∠ABC），∵∠A+∠ABC=∠ACD，∴∠A=∠ACD-∠ABC，∴∠A1=∠A，∴∠A1=×96°=48°，∵∠A1=∠A，∠A2=∠A1=∠A，…以此类推∠A2012=∠A=62．⑴略；⑵（5，0）；⑶；⑷；【解析】（1）线段AB绕点A按逆时针方向旋转90°得到线段AC．线段AC及点B经过的路径是一段弧，根据弧长公式计算路径；（2）根据点A的坐标为（1，3），点B的坐标为（-2，-1），可建立直角坐标系，从直角坐标系中读出点C的坐标为（5，0）；（3）线段AB在旋转到线段AC的过程中，线段AB扫过的区域的面积为一个扇形，根据扇形公式计算；（4）将它围成一个几何体即圆锥的侧面，则该几何体底面圆的周长就等于弧长，利用此等量关键可计算出半径．63．4050【解析】略答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。64．当n=3时分成7部分；…………………2′当n=4时分成11部分；…………………4′之间的关系是…………………8′【解析】略【答案】易证∠A+∠E=180°∠B+∠C+∠D=360°∴β=2α【解析】略66．略【解析】略67．（作出角平分线得3分，作出半圆再得2分，小结1分，共6分）解：如图即为所求作图形【解析】略68．见解析【解析】本题考查的是平行线的判定与性质根据平行线的性质：两直线平行，同旁内角互补，得到：若（1）AB∥DC则有（4）∠B+∠C=180；由（2）AD∥BC可以得到（3）∠A+∠B=180°．反之，根据平行线的判定，也成立．连接BD，则BD截AD和BC，因而可以得到：若AD∥BC，则可以得到∠ADB=∠DBC．以一个作题设，一个作结论，写出一个真命题是：若AB∥DC则有∠B+∠C=180；若连接BD，写出一个真命题是：若AD∥BC，则可以得到∠ADB=∠DBC．证明：∵AD∥BC，∴∠ADB=∠DBC（两直线平行，内错角相等）．69．解：探究2结论：∠BOC=理由如下：∵BO和CO分别是∠ABC和∠ACD的角平分线答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。探究3：结论∠BOC=90°－拓展：结论【解析】（1）根据提供的信息，根据三角形的一个外角等于与它不相邻的两个内角的和，用∠A与∠1表示出∠2，再利用∠O与∠1表示出∠2，然后整理即可得到∠BOC与∠O的关系；（2）根据三角形的一个外角等于与它不相邻的两个内角的和以及角平分线的定义表示出∠OBC与∠OCB，然后再根据三角形的内角和定理列式整理即可得解．（3）拓展：结论.70．解：.理由是【解析】只要得出∠B=∠C，就可以证明AB=AC；由AE平分∠DAC得出∠DAE=∠CAE，由两直线平行，内错角、同位角分别相等可以得出∠CAE=∠C，∠DAE=∠B，即可证∠C=∠B，所以AB=AC．71．（1）∠MON=60°（理由略）；（2）由题意，∠BOD=105°-10x°；∠AOC=15°+10x°；∴∠BOC=135°-10x°，∠AOD=45°+10x°，∵∠AOM：∠BON=7：11，且OM、ON分别平分∠AOD、∠BOC，∴∠AOD：∠BOC=7：11，即（45°+10x°）：（135°-10x°）=7：11；解之得x=2.5【解析】（1）根据∠AOC=60°，∠DOC=30°，得出∠DOC、∠DOM和∠MOC的度数，再根据∠AOC=60°，∠AOB=150°，得出∠BOC、∠NOC和∠NOD=45°-30°的度数，即可求出∠MOC=∠NOD；（2）①如图（1）所示，按题意，∠MON=∠MOD+∠NOC-∠COD=（∠AOD+∠BOC）-∠COD=答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。（∠AOB+∠COD）-∠COD=60°，即∠MON=60°；②先令∠MOC=∠AOC=x，得出∠DOM=30°-x，求出x的值，即可求出∠DOM、∠NOD和∠AOC的值，即可求出∠NOD与∠MOC的数量关系．72．已知；两直线平行，同旁内角互补；两直线平行，同旁内角互补；等量代换.【解析】根据平行线的性质即可证得。73．【解析】（1）根据点M、N分别是AC、BC的中点，先求出MC、CN的长度，再利用MN=CM+CN即可求出MN的长度即可，（2）根据点M、N分别是AC、BC的中点，可知CM=AC，CN=BC，再利用MN=CM+CN即可求出MN的长度．74．【解析】由∠AOB=110°，∠COD=70°，易得∠AOC+∠BOD=40°，由角平分线定义可得∠AOE+∠BOF=40°，那么∠EOF=∠AOB+∠AOE+BOF．75．解：作图如下：答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。【解析】根据线段的和、差的作法，先作出2a的长度，然后在2a上作出b的长度，即可得到2a-b．76．解：如图所示．【解析】根据线段，延长线和反向延长线的基本作图方法直接进行画图即可．77．解：当OC落在∠AOB内部时，如下图①由∠AOC=∠BOC得：∠AOC=80°×=30°当OC落在∠AOB外部时，如下图②，反向延长OA、OB。若OC落在∠BON内，此时∠AOC＞∠BOC，而∠AOC=∠BOC，这不可能，舍去。若OC落在∠MOA内部时，则∠BOC-∠AOC=80°，且∠AOC∶∠BOC=3∶5，∠BOC=200°＞180°，舍去.答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。若OC落在∠MON内部时，此时，∠AOC+∠BOC=360°–80°=280°，故∠AOC=280°×=105°.综上所述，∠AOC=30°或105°.【解析】首先根据题意画出图形，然后跟情况进行讨论解答，（1）当OC落在∠AOB内部时，如下图①，（2）当OC落在∠AOB外部时，如下图②：①若OC落在∠BON内，根据图形推出AOC＞∠BOC，由∠AOC=∠BOC，可知这种情况不存在，②若OC落在∠MOA内部时，根据图形可知∠BOC-∠AOC=80°，由∠AOC：∠BOC=3：5，推出∠BOC=200°＞180°，可知这种情况也不存在，③若OC落在∠MON内部时，根据周角的定义和∠AOC：∠BOC=3：5，即可推出结果，综合所分析的结果即可推出∠AOC的度数．78．解：设这个角为x，依题意可得方程：90º-x=解得：答：所求的这个角为30度.【解析】设这个角为x，即可表示出它的余角和补角，根据余角和补角的关系列出方程即可求得这个角。【题型】解答题79．（1）155°（2）OE平分∠BOC【解析】解：(1)∵OD平分∠AOC∴∠AOD=∠DOC=∠AOC=50°=25°…………………(2分)∴∠BOD=180°-∠AOD=180°-25°=155°………………(2分)（2）∵∠DOE=90°∠DOC=25°∴∠COE=∠DOE-∠DOC=90°-25°=65°………………(2分)又∵∠BOE=∠BOD-∠DOE=155°-90°=65°∴∠COE=∠BOE即OE平分∠BOC………………………………………………(2分)（1）由角平分线的性质即可推出∠AOD=25°，然后根据邻补角的性质即可推出∠BOD的度数，（2）首先根据垂线的性质和（1）所得的结论，即可推出∠COE和∠BOE的度数，然后根据角平分线的定义即可确定OE平分∠BOC．80．（1）；（2）能，因为∠AOB＝900，∠BOC＝，所以∠AOC＝900＋，因为OM、ON平分∠AOC,∠BOC的线所以∠MOC＝∠AOC＝(900＋)＝450＋x所以∠CON＝∠BOC＝x所以∠MON＝∠MOC－∠CON＝450＋x－x＝450答案第17页，总18页\n本卷由【在线组卷网www.zujuan.com】自动生成，请仔细校对后使用，答案仅供参考。（3）能，因为∠AOB＝，∠BOC＝，所以∠AOC＝＋，因为OM、ON平分∠AOC,∠BOC的线所以∠MOC＝∠AOC＝(＋)所以∠CON＝∠BOC＝所以∠MON＝∠MOC－∠CON＝(＋)－＝即．【解析】（1）根据角平分线的以求出∠MOC与∠NOC的度数，然后相减即可求出∠MON的度数；（2）根据（1）的求解思路，先利用角平分线的定义表示出∠MOC与∠NOC的度数，然后相减即可得到∠MON的度数；（3）根据前两题的求解思路把具体数据换为α、β，然后整理即可得出规律．81．（1）∵∠BMF+∠EMB=180°∴∠BMF=180°-∠EMB∵∠EMB=50°∴∠BMF=180°-50°=130°∵MG平分∠BMF∴∠BMG=∠GMN=∠BMF=65°∵AB∥CD∴∠1=∠BMG=65°（2）∵∠MNC=∠1+∠GMN∴∠1=∠MNC-∠GMN∵∠MNC=140°，∠GMN=65°∴∠1=140°-65°=75°【解析】（1）根据两角互补及角平分线的性质可求出∠BMG的度数，再根据平行线的性质即可求解；（2）先根据两角互补及角平分线的性质可求出∠NMG的度数，再由三角形内角与外角的性质及∠MNC=140°即可求出∠1的度数．82．∠AOC=140°【解析】根据图形即可推出∠EOD=∠BOC=50°，由∠DOB=90°，可求出∠AOB=90°，即可求出∠AOC的度数．83．（1）图略(2)图略(3)OA，垂线段CP的长度，PH

查看更多