初中数学测试题(含答案)
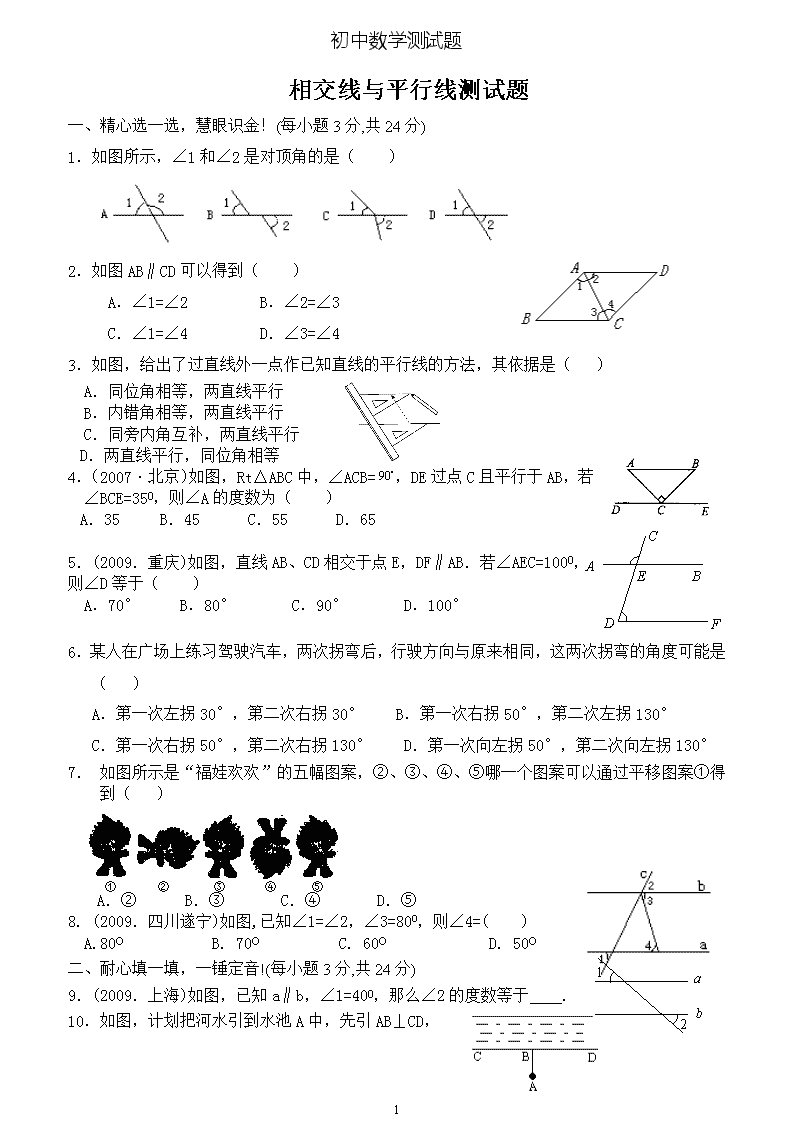
初中数学测试题相交线与平行线测试题一、精心选一选,慧眼识金!(每小题3分,共24分)1.如图所示,∠1和∠2是对顶角的是()2.如图AB∥CD可以得到()A.∠1=∠2B.∠2=∠3C.∠1=∠4D.∠3=∠43.如图,给出了过直线外一点作已知直线的平行线的方法,其依据是()A.同位角相等,两直线平行B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.两直线平行,同位角相等4.(2007·北京)如图,Rt△ABC中,∠ACB=,DE过点C且平行于AB,若∠BCE=350,则∠A的度数为( )CAEBFDA.35B.45C.55D.655.(2009.重庆)如图,直线AB、CD相交于点E,DF∥AB.若∠AEC=1000,则∠D等于()A.70°B.80°C.90°D.100°6.某人在广场上练习驾驶汽车,两次拐弯后,行驶方向与原来相同,这两次拐弯的角度可能是()A.第一次左拐30°,第二次右拐30°B.第一次右拐50°,第二次左拐130°C.第一次右拐50°,第二次右拐130°D.第一次向左拐50°,第二次向左拐130°7.如图所示是“福娃欢欢”的五幅图案,②、③、④、⑤哪一个图案可以通过平移图案①得到()A.②B.③C.④D.⑤8.(2009.四川遂宁)如图,已知∠1=∠2,∠3=80O,则∠4=()A.80OB.70OC.60OD.50O12ab二、耐心填一填,一锤定音!(每小题3分,共24分)9.(2009.上海)如图,已知a∥b,∠1=400,那么∠2的度数等于.10.如图,计划把河水引到水池A中,先引AB⊥CD,42\n初中数学测试题垂足为B,然后沿AB开渠,能使所开的渠道最短,这样设计的依据是_________________________________________.11.如图,直线AB、CD相交于点O,∠1-∠2=64°,则∠AOC=______.12.如图,一张宽度相等的纸条,折叠后,若∠ABC=110°,则∠1的度数为_________.13.把命题“锐角的补角是钝角”改写成“如果……,那么……”的形式是:______________________________________.14.(2007.金华)如图,直线AB∥CD,EF⊥CD,F为垂足。如果∠GEF=20,那么∠1的度数是.15.(2009.湖南常德)如图,已知AE∥BD,∠1=130o,∠2=30o,则∠C=.16.(2006·长春)将直尺与三角尺按如图所示的方式叠放在一起,在图中标记的角中,所有与∠1互余的角一共有 个。三、用心做一做,马到成功!(本大题共52分)17.(8分)如图所示,AD∥BC,∠1=78°,∠2=40°,求∠ADC的度数.18.(8分)如图,直线AB、CD相交于O,OD平分∠AOF,OE⊥CD于点O,∠1=50°,求∠COB、∠BOF的度数.42\n初中数学测试题19.(8分)如图14,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏西111°32′。如果A、B两地同时开工,那么在B地按北偏东多少度施工,才能使公路在山腹中准确接通?为什么?AEBCDF20.(8分)如图,BD是∠ABC的平分线,ED∥BC,∠FED=∠BDE,则EF也是∠AED的平分线。完成下列推理过程:证明:∵BD是∠ABC的平分线(已知)∴∠ABD=∠DBC()∵ED∥BC(已知)∴∠BDE=∠DBC()∴(等量代换)又∵∠FED=∠BDE(已知)∴∥()∴∠AEF=∠ABD()∴∠AEF=∠DEF(等量代换)∴EF是∠AED的平分线()21.(9分)已知:如图,AB//CD,试解决下列问题:(1)∠1+∠2=______;(2分)(2)∠1+∠2+∠3=_____;(2分)(3)∠1+∠2+∠3+∠4=_____;(2分)42\n初中数学测试题(4)试探究∠1+∠2+∠3+∠4+…+∠n=;(4分)22.(11分)已知AD与AB、CD交于A、D两点,EC、BF与AB、CD交于E、C、B、F,且∠1=∠2,∠B=∠C(如图).(1)你能得出CE∥BF这一结论吗?(2)你能得出∠B=∠3和∠A=∠D这两个结论吗?若能,写出你得出结论的过程.七年级数学第一章测试卷一、选择题:(每题2分,共30分)1.下列说法正确的是()A.所有的整数都是正数B.不是正数的数一定是负数C.0不是最小的有理数D.正有理数包括整数和分数2.的相反数的绝对值是()42\n初中数学测试题A.-B.2C.-2D.3.有理数a、b在数轴上的位置如图1-1所示,那么下列式子中成立的是()A.a>bB.a
0D.4.在数轴上,原点及原点右边的点表示的数是()A.正数B.负数C.非正数D.非负数5.如果一个有理数的绝对值是正数,那么这个数必定是()A.是正数B.不是0C.是负数D.以上都不对6.下列各组数中,不是互为相反意义的量的是()A.收入200元与支出20元B.上升10米和下降7米C.超过0.05mm与不足0.03mD.增大2岁与减少2升7.下列说法正确的是()A.-a一定是负数;B.│a│一定是正数;C.│a│一定不是负数;D.-│a│一定是负数8.如果一个数的平方等于它的倒数,那么这个数一定是()A.0B.1C.-1D.±19.如果两个有理数的和除以它们的积,所得的商为零,那么,这两个有理数()A.互为相反数但不等于零;B.互为倒数;C.有一个等于零;D.都等于零10.若0b>0B.b>c>a;C.b>a>cD.c>a>b15.若│x│=2,│y│=3,则│x+y│的值为()A.5B.-5C.5或1D.以上都不对二、填空题:(每空2分,共30分)16.某地气温不稳定,开始是6℃,一会儿升高4℃,再过一会儿又下降11℃,这时气温是__.17.一个数的相反数的倒数是,这个数是________.18.数轴上到原点的距离是3个单位长度的点表示的数是______.19.-2的4次幂是______,144是__________的平方数.20.若│-a│=5,则a=________.21.若ab>0,bc<0,则ac________0.22.绝对值小于5的所有的整数的和_______.23.用科学记数法表示13040000应记作_______________________,若保留3个有效数字,则近似值为__________.24.若│x-1│+(y+2)2=0,则x-y=___________;25.(-5)×=_________.42\n初中数学测试题26.=___________;27.=___________.28.=_______.三、解答题:(共60分)29.列式计算(每题5分,共10分)(1)-4、-5、+7三个数的和比这三个数绝对值的和小多少?(2)从-1中减去的和,所得的差是多少?30.计算题(每题5分,共30分)(1)(-12)÷4×(-6)÷2;(2);(3);(4);(5);(6)1+3+5+…+99-(2+4+6+…+98).42\n初中数学测试题31.若│a│=2,b=-3,c是最大的负整数,求a+b-c的值.(10分)32.检修组乘汽车,沿公路检修线路,约定向东为正,向西为负,某天自A地出发,到收工时,行走记录为(单位:千米):+8、-9、+4、+7、-2、-10、+18、-3、+7、+5回答下列问题:(每题5分,共10分)(1)收工时在A地的哪边?距A地多少千米?(2)若每千米耗油0.3升,问从A地出发到收工时,共耗油多少升?答案:一、1.C2.D3.A4.D5.B6.D7.C8.B9.A10.B11.A12.C13.D14.C15.C二、16.评析:负数的意义,升高和降低是一对意义相反的量,借助数轴可以准确无误地得出正确结果-1℃,数无数不形象,形无数难入微,42\n初中数学测试题数形结合是数学的基本思想,在新课标中有重要体现,是中考命题的重要指导思想,多以综合高档题出现,占分比例较大.17.评析:利用逆向思维可知本题应填.18.评析:绝对值的几何意义.在数轴上绝对值的代名词就是距离,绝对值是一个“一学就会一做就错”的难点概念,其原因是没有把握好绝对值的几何意义.19.1620.评析:可以设计两个问题理解本题.①什么数的绝对值等于5,学生可顺利得出正确结论±5.②什么数的相反数等于±5,学生也可顺利得出正确结论-5和5,在解题的过程中学生自然会概括出│-a│=│a│,把一个问题转化成两个简单的问题,这种方法和思想是数学学习的核心思想,这一思想在历届中考中都有体现.21.<22.023.用科学记数法表示一个数,要把它写成科学记数的标准形式a×,这里的a必须满足1≤a<10条件,n是整数,n的确定是正确解决问题的关键,在这里n是一个比位数小1的数,因为原数是一个8位数,所以可以确定n=7,所以13040000=1.304×107,对这个数按要求取近似值,显然不能改变其位数,只能对其中的a取近似值,保留3个有效数字为1.30×107,而不能误认为1.30,通过这类问题,学生可概括出较大的数取近似值的基本模式应是:先用科学记数法将其表示为a×(1≤a<10,n是整数),然后按要求对a取近似值,而n的值不变.24.325.2126.27.28.4三、29.本题根据题意可列式子:(1)(│-4│+│-5│+│7│)-(-4-5+7)=18.42\n初中数学测试题(2).30.(1)属同一级运算,计算这个题按题的自然顺序进行(-12)÷4×(-6)÷2=(-12)××(-6)×=9.(2)是一个含有乘方的混合运算=.这里把-4同0.25结合在一起,利用了凑整法可以简化计算.(3)这一题只含同一级运算,计算中要统一成加法的计算,然后把可以凑整的结合在一起进行简便计算,具体做法是:==(4)本题是一个混合运算题,具体解法如下:==(5)==(6)1+3+5+…99-(2+4+6+…+98)42\n初中数学测试题=1+(3-2)+(5-4)+…(99-98)=1+1+1+…1=50.此题有多种简便方法,请你探索.31.∵│a│=2,∴a=±2,c是最大的负整数,∴c=-1,当a=2时,a+b-c=2-3-(-1)=0;当a=-2时a+b-c=-2-3-(-1)=-4.32.(1)∵8-9+4+7-2+10+18-3+7+5=8+4+7+18+7+5-9-10-2-3=25,∴在A处的东边25米处.(2)∵│8│+│-9│+│4│+│7│+│-2│+│-10│+│18│+│-3│+│7│+│5│=73千米,73×0.3=21.9升,∴从出发到收工共耗油21.9升.第十四、十五章模拟测试题姓名班级一、选择题(每小题3分,共30分)1、直线y=x+3与y轴的交点坐标是()A.(0,3) B.(0,1) C.(3,O) D.(1,0)2、以方程为解的点(x,y)在平面直角坐标系中的位置是( )A.第一象限 B.第二象限 C.第三角限 D.第四象限3、下列各曲线中,不能表示y是x的函数的是( )42\n初中数学测试题A. B. C. D.4、y=(m+3)x+2是一次函数,且y随自变量x的增大而减小,那么m的取值是( )A.m<3 B.m<-3 C.m=3 D.m≤-35、已知正比例函数()的函数值随的增大而增大,则一次函数的图象大致是( ) 6、对于函数y=2x-1,当自变量增加m时,相应的函数值增加 ( ) A.2m B.2m-1 C.m D.2m+17、 直线y=kx+b与两坐标轴的交点如图所示,当y<0时,x的取值范围是()A.x>2 B.x<2 C.x>-1 D.x<-18、 当x=5时一次函数y=2x+k和y=3kx-4的值相同,那么k和y的值分别为( )A.1,11 B.-1,9 C.5,11 D.3,39、已知点,(2,y2)都在直线y=-x+2上,则y1、y2大小关系是( )(A)y1>y2 (B)y1=y2 (C)y1-3 (B)x<-3 (C)x>3 (D)x<3二、填空题(每空?分,共?分)42\n初中数学测试题19、用描点法画函数图象的一般步骤是 。17、由3x-2y=5可得到用x表示y的式子是 .18、函数关系式中的自变量的取值范围是 。20、弹簧的长度y(cm)与所挂物体的质量x(kg)的关系是一次函数,图象如右图所示,则弹簧不挂物体时的长度是___________cm; 21、如图三,直线与轴、轴分别交于、两点,把△绕点顺时针旋转90°后得到△,则点的坐标是 ▲ . 22、函数y=-2x+3的图像是由直线y=-2x向 平移 个单位得到的。23、已知函数是一次函数,则m=__________.24、若函数y=4x+3-k的图象经过原点,那么k= 。25、若点P(a,b)在第二象限内,则直线y=ax+b不经过第_____限26、当x=_________时,函数y=3x+1与y=2x-4的函数值相等。27、直线y=-x+a与直线y=x+b的交点坐标为(m,8),则a+b=______.42\n初中数学测试题28、图是一次函数的图象,则关于x的不等式的解集为_________________. 29、孔明同学在解方程组的过程中,错把看成了6,他其余的解题过程没有出错,解得此方程组的解为,又已知直线过点(3,1),则的正确值应该是 .30、已知某个一次函数的图象与x轴、y轴的交点坐标分别是(-2,0)、(0,4),则这个函数的解析式为 .31、已知:一次函数的图象与直线平行,并且经过点 ,那么这个一次函数的解析式是___________________.32、(2009年桂林市、百色市)如图,是一个正比例函数的图像,把该图像向左平移一个单位长度,得到的函数图像的解析式为 . 12、当时,;13、下面计算:中,其中错误的结果的个数是________42\n初中数学测试题14、计算:= .15、已知:,,化简的结果是 .16、.观察下列等式:,,,……(1)猜想并写出第n个等式;(2)证明你写出的等式的正确性.17、已知则____________.18、如果x2-2(m+1)x+m2+5是一个完全平方式,则m= ;19、若x-y=3,x·y=10,则x2+y2=______.20、________________;21、(2x-3)( )=4x2-9.22、计算:=________.23、若3n=2,3m=5,则32m+n-1=___________.24、计算:(-2xy2)2・3x2y÷(-x3y4)=____________22、分解因式:x2-9= ▲ .23、分解因式: .24、实数x、y满足,则x—y= __________.25、(2010四川乐山)下列因式分解:①;②;③;④.其中正确的是_______.(只填序号)42\n初中数学测试题26、·( )=—.27、若展开后不含x的一次项,则m=____________.28、=____________。29、化简= .30、计算:=________________.31、计算:(-2xy2)2・3x2y÷(-x3y4)=____________。32、计算:=___________. 33、计算:=________.34、(2x-3)( )=4x2-9.35、如图是由边长为a和b的两个正方形组成,通过用不同的方法,计算下图中阴影部分的面积,可以验证的一个公式是 .36、已知a2+b2=13,ab=6,则a+b的值是________.三、计算、简答题(每空?分,共?分)26、已知,求n的值.27、 28、计算:.29、计算: .30、化简:(a+1)(a-1)-a(a-1).42\n初中数学测试题31、先化简,再求值:,其中32、化简:33、化简:34、先化简,再求值。 ,其中.35、先化简,再求值,其中;36、化简:.37、先化简再求值:[(x+2y)(x-2y)-(x+4y)2]÷(4y),其中x=5,y=2.38、已知求代数式的值。39、计算(-1)2009+(3.14)0++12、先化简,再求值:[(x+2y)2-2y(x+2y)-8xy]÷2x,其中x=-4,y=1.13、因式分解 ; 14、分解因式: .15、因式分解:2x3y-8x2y2+8xy3.16、.因式分解:42\n初中数学测试题17、计算题: ;18、先化简,再求值:(本小题4分),其中,.19、计算:20、化简:.21、计算33、在一次运输任务中,一辆汽车将一批货物从甲地运往乙地,到达乙地卸货后返回.设汽车从甲地出发(h)时,汽车与甲地的距离为(km),与的函数关系如图所示.根据图象信息,解答下列问题:(1)这辆汽车的往、返速度是否相同?请说明理由;(2)求返程中与之间的函数表达式;(3)求这辆汽车从甲地出发4h时与甲地的距离.34、 已知直线y=(5-3m)x+m-4与直线y=x+6平行,求此直线的解析式。35、 已知函数y=(8—2m)x+m-2(1)若函数图象经过原点,求m的值(2)若这个函数是一次函数,且y随着x的增大而减小,求m的取值范围.(3)若这个函数是一次函数,且图象经过一、二、三象限,求m的取值范围.36、已知羊角塘服装厂有A种布料70m,B种布料52m,现计划用这两种布料生产甲、乙两种型号的时装共80套,已知做一套甲型号的时装需用A种布料0.6m,B种布料0.9m,可获利润45元;做一套乙型号的时装需用A种布料1.1m,B种布料0.4m,可获利润50元,若生产乙型号的时装x套,用这批布料生产这两种型号的时装所获的总利润为y元。42\n初中数学测试题 (1)求y(元)与x(套)之间的函数关系式,并求自变量x的取值范围; (2)羊角塘服装厂在生产这批时装时,当乙型号的时装为多少套时,所获总利润最大?最大总利润是多少?四、计算题(每空?分,共?分)37、如下图是某汽车行驶的路程S(km)与时间t(min)的函数关系图。观察图中所提供的信息,解答下列问题: (1)汽车在前9分钟内的平均速度是多少?(2)汽车在中途停了多久?(3)当16≤t≤30时,求S与t的函数关系式.五、综合题(每空?分,共?分)38、某商场欲购进A、B两种品牌的饮料共500箱,此两种饮料每箱的进价和售价如下表所示。设购进A种饮料箱,且所购进的两种饮料能全部卖出,获得的总利润为元。品牌AB进价(元/箱)5535售价(元/箱)6340(1)求关于的函数关系式;(2)如果购进两种饮料的总费用不超过20000元,那么该商场如何进货才能获利最多?并求出最大利润。(注:利润=售价-进价)4、下面是按一定规律排列的一列数:第1个数:;第2个数:;42\n初中数学测试题第3个数:;……第个数:.那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是( )A.第10个数 B.第11个数 C.第12个数 D.第13个数评卷人得分二、计算题(每空?分,共?分)5、先化简,再求值:,其中.7、柜台上放着一堆罐头,它们摆放的形状见图:第一层有听罐头,第二层有听罐头,第三层有听罐头,……根据这堆罐头排列的规律,第(为正整数)层有 听罐头(用含的式子表示).6、阅读下面的材料: ①,反过来,得42\n初中数学测试题②,反过来,得③,反过来,得利用上面的材料中的方法和结论计算下题: 先化简,再求值:,其中.1、已知,如图,延长的各边,使得,,顺次连接,得到为等边三角形.求证:(1);(2)为等边三角形.2、如图所示,在△ABC中,∠A=90°,DE⊥BC,BD平分∠ABC,AD=6cm,BC=15cm,△BDC的面积为___________cm2.安洲中学七年级第二章整式加减测试题班级:号次:姓名:一、选择题:(每小题3分,共30分)42\n初中数学测试题1、原产量n吨,增产30%之后的产量应为()A、70%n吨B、130%n吨C、n+30%吨D、30%n吨2、买一个足球需要m元,买一个篮球需要n元,则买4个足球和7个篮球共需要多少元()元A、4m+7nB、28mnC、7m+4nD、11mn3、下列各组式子中,是同类项的是()A、与B、与C、与D、与4.单项式的系数和次数分别是( )A、-3π,5 B、-3,7 C、-3π,6 D、-3,6 5、下列说法中正确的是()A、5不是单项式B、是单项式 C、的系数是0D、是整式6、下列各式中,正确的是()A、B、C、D、7、将合并同类项得()A、B、C、D、8.已知和是同类项,则m的值是( )A、1 B、2 C、3 D、49.如果一个多项式是五次多项式,那么它任何一项的次数()A、都小于5 B、都等于5C、都不小于5D、都不大于510.若代数式2x2+3y+7的值为8,那么代数式6x2+9y+8的值为()A、1 B、11 C、15 D、23二、填空:(每格3分,共18分)11、计算:12.单项式的系数是,次数是.13.多项式是_______次_______项式.14.三个连续偶数中,2n是中间的一个,这三个数的和为 .15.已知轮船在静水中前进的速度是千米/时,水流的速度是2千米/时,则这轮船在逆水中航行2小时的路程是千米.16.如右上图,将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,……如此继续下去,结果如下表:所剪次数1234…n42\n初中数学测试题正三角形个数471013…an则an=________________(用含n的代数式表示)三、解答题(共52分,要有解答步骤。)17.计算:(每题4分)(1);(2)st+4+3st-4(3)2(2+3)-3(2-)(4)-[-4+(-)]-2(以下每题6分,共36分)18、化简求值:.19、已知三角形第一边长为(2+)cm,第二边比第一边长(-)cm,第三边比第一边短cm,求这个三角形的周长.(1)填空:第二边的长度为cm,第三边的长度为cm(2)求三角形的周长.42\n初中数学测试题20、某工厂第一车间有人,第二车间比第一车间人数的少30人,如果从第二车间调出10人到第一车间,那么:(1)两个车间共有人?(2)调动后,第一车间的人数为人,第二车的人数为人;(3)求调动后,第一车间的人数比第二车的人数多几人?21、人在运动时心跳次数通常和人的年龄有关.用表示一个人的年龄,用表示正常情况下,这个人在运动时承受的每分钟心跳的最高次数,则.(1)正常情况下,在运动时一个14岁少年所能承受的每分钟心跳的最高次数是多少?(2)一个45岁的人运动时,10秒心跳的次数为22次,请问他有危险吗?为什么?23、(10分)仙居三江超市出售一种商品,其原价元,现有两种调价方案:方案(1)先提价20%,再降价20%;方案(2)先降价20%,再提价20%;(1)请分别计算两种调价方案的最后结果。(2)如果调价后商品的销售数量都一样,请直接回答该选择那种调价方案赚的利润多?24、张华在一次测验中计算一个多项式加上时,不小心看成减去,计算出错误结果为,试求出原题目的正确答案。一次函数综合测试题(一)一、选择题。(3分×10)42\n初中数学测试题1、已知一次函数,若随着的增大而减小,则该函数的图像经过:A.第一、二、三象限B.第一、二、四象限C.第二、三、四象限D.第一、三、四象限2、若函数是一次函数,则的值为:A.B.的全体实数C.全体实数D.不能确定3、如图,有一个装有进、出水管的容器,单位时间内进、出的水量都是一定的,已知容器的容积为600L,又知单开进水管10min可以把容器注满,若同时打开进、出水管,20min可以把满容器的水放完,现已知水池内有水200L,先打开进水管5min,再打开出水管,两管同时开放,直到把容器中的水放完,则正确反映这一过程中容器的水量Q(L)随时间t(min)变化的图像是:t/min5Q/L200500Q/L0t/min2005005t/minQ/L02005500t/minQ/L020050ABCD4、无论为何实数,直线与直线的交点不可能在:A.第三象限B.第四象限C.第一象限D.第二象限5、与的图像交于轴上一点,则为:A.2B.C.D.6、已知两个一次函数的图像重合,则一次函数的图像所经过的象限为:A.第一、二、三象限B.第二、三、四象限C.第一、三、四象限D.第一、二、四象限S/cm2F/N07、两个物体A、B所受的压强分别为与(P)(、为常数),它们所受压力F(N)与受力面积S(㎡)的函数关系图像分别是射线、,(公式),如图所示,则:A.>B.<C.≥D.≤xyxyxyxyABCD8、下列四个图像,不表示某一函数图像的是:9、若<0,且的图像不过第四象限,则点(c)所在象限为()A、一B、二C、三D、四10、如果一次函数当自变量的取值范围是-1<<3时,函数y的取值范围是-2<<6,那么此函数解析式为:A、B、C、或D、或二、填空题。(3分×8)42\n初中数学测试题11、某种储蓄的月利率是0.2%,存入100元本金后,则本息和y(元)与储存月数x之间的函数关系为:________________12、已知正比例函数的图象经过第二、四象限,则m=_____________13、直线向上平移3个单位,再向左平移2个单位后直线解析式为:_____________14、已知函数,则自变量x的取值范围是:_____________15、某风景区集体门票的收费标准是:20人以内(含20人),每人25元;超过20人,超过部分,每人10元,写出应收门票y(元)与游览人数(人)之间的函数关系式________________。利用该函数关系计算某班54名学生去该风景区游览时,购门票共花了_______元。16、关于的一次函数的图像与y轴的交点在轴的上方,则y随的增大而减小,则a的取值范围是。17、在弹性限度内,一弹簧长度(cm)与所挂物体的质量x(kg)之间的函数关系是,如果该弹簧最长可以拉伸到20cm,则它所挂物体的最大质量是________________。18、2与成正比例,且=3时,1,则与的函数关系式为________________。三、解答题。(66分)19、已知一次函数的图像交x轴于A(-6,0),交正比例函数图像于B,且B在第二象限,其横坐标是-4,若△AOB的面积是15(平方单位),求正比例数和一次函数的解析式。(8分)AB20、如图,已知直线的图象与x轴、y轴交于A、B两点,直线经过原点与线段AB交于点C,且把△AOB的面积分成2:1两部分,求直线的解析式。(8分)21、如图,表示甲、乙两名选手在一次自行车越野赛中,路程y(km)随时间(min)变化的图象(全程)根据图像回答。(12分)334348155Oy(km)765(1)比赛开始多少分钟时,两人第一次相遇?(2)这次比赛全程多少千米?(3)比赛开始多少分钟时,两人第二次相遇?22、(8分)直线过点A(-1,5)且平行于直线。42\n初中数学测试题(1)求这条直线的解析式;(2)若点B(m,-5)在这条直线上,O为坐标原点,求m及△AOB的面积。23、121484O5/hy/㎡2535(8分)某贮水塔在工作期间,每小时的进水量与出水量都是固定不变的,每日从凌晨4点到8点只进水,不出水;8点到12点既进水又出水;14点至次日凌晨只出水不进水,经测定,水塔中贮水量y(m3)与时间(h)的函数关系如图所示。(1)求每小时的进水量;(2)当8≤≤12时,求y与的函数关系式;(3)当14≤≤18时,求y与的函数关系式。24、(10分)如图所示,直线,相交于点A,与轴的交点坐标为(-1,0),与y轴的交点坐标为(0,-2),结合图像解答下列题:-3-1-243211234Ay(1)求出直线表示的一次函数的表达式。(2)当为何值时,,表示的两个一次函数值都大于0?LBLA710t/miny/海里0525、(12分)某边防部队接到情报,近海处有一可疑船只A正向公海方向行驶,边防部队迅速派出快艇B追赶,在追赶过程中,设快艇B相对于海岸的距离为y1(海里),可疑船只A相对于海岸的距离为y2(海里),追赶时间为t(min),图中、分别表示y2、y1与t之间的关系,结合图像回答下列问题:(1)请你根据图中标注的数据,分别求出y2、y1与t之间的函数关系式,并写出自变量的取值范围。(2)15分钟内B能否追上A?说明理由。(3)已知当A逃到距海岸12海里的公海时,B将无法对其进行检查,照此速度计算,B能否在A逃入公海前将其拦截?42\n初中数学测试题一次函数测试题四川邹川东一、选择题:1、下列函数中,是正比例函数的是(B)A、y=B、y=C、y=D、y=2、在函数y=,y=,y=,y=x+8中,一次函数有(B)A、1个B、2个C、3个D、4个3、若函数y=(m+1)+2是一次函数,则m的值为(C)A、m=±1B、m=-1C、m=1D、m≠-14、已知直线y=2x与直线y=kx+3互相平行,则k的值为(B)A、k=-2B、k=2C、k=±2D、无法确定k的值5、一次函数y=kx+b,若k+b=1,则它的图象必经过点(D把数带进去)A、(-1,-1)B、(-1,1)C、(1,-1)D、(1,1)6、下列各组函数中,与y轴的交点相同的是(C)A、y=5x与y=2x+3B、y=-2x+4与y=-2x-4C、y=+3与y=-2x+3D、y=4x-1与y=x+17、已知函数y=(+2)x,y随x增大而(A)A、增大B、减小C、与m有关D、无法确定8、若一次函数y=(1-2m)x+3的图象经过A(,)和B(,),当<时,<,则m的取值范围是A、m<0B、m>0C、m<D、m>(C)9、已知直线y=中,若ab>0,ac<0,那么这条直线不经过(B)A、第一象限B、第二象限C、第三象限D、第四象限10、直线y=-2x+b与两坐标轴围成的三角形的面积为4,则b的值为(C)A、4B、-4C、±4D、±2二、填空题:1、一次函数y=2x+6的图象与y轴相交,则交点坐标为(0,6)2、已知一次函数y=kx+b的图象经过(-1,1)、(2,3)两点,则这个一次函数的关系式为3、将直线y=3x-1向上平移3个单位,得直线_。4、一次函数的图象经过点P(1,3),且y随x的增大而增大,写出一个满足条件的函数关系式_。5、已知点A(1,a)在直线y=-2x+3上,则a=_。42\n初中数学测试题6、已知点P在直线y=上,且点P到y轴的距离等于3个单位长度,则点P的坐标为_。7、某个一次函数y=kx+b的图象位置大致如下图(1)所示,则k的取值范围为_,b的取值范围为_。(图1)(图2)8、(2006·绍兴)如图(2),一次函数y=x+5的图象经过P(a,b)和Q(c,d),则a(c-d)-b(c-d)的值为_。9、(2006·杭州)已知y是x的一次函数,下表中列出了部分对应值,则m=_。x-101y1m-110、点A(2,a)在一次函数y=-x+3的图象上,且一次函数的图象与y轴的交点为B,则△AOB的面积为_。三、解答题:1、直线=kx+b与y轴的交点和直线=2x+3与y轴的交点相同,直线与x轴的交点和直线与x轴的交点关于原点对称,求:直线的关系式。2、已知y=+,与x+2成正比,是x+1的2倍,并且当x=0时,y=4,试求函数y与x的关系式。3、已知直线y=-x+4与直线y=2x-2相交于点A,且直线y=-x+4与y轴相交于点B,直线y=2x-2与x轴相交于点C,求四边形ABOC的面积。4、已知一次函数y=kx+b的自变量x的取值范围是-1≤x≤5,相对应的函数值范围为-6≤y≤0,求此函数的关系式。5、(2006·衡阳)为了鼓励市民节约用水,自来水公司特制定了新的用水收费标准,每月用水量x(吨)与应付水费(元)的函数关系如图所示。(1)求出当月用水量不超过5吨时,y与x之间的函数关系式;(2)某居民某月用水量为8吨,求应付水费是多少?42\n初中数学测试题(图3)6、已知一次函数y=-x+12。(1)求其图象与坐标轴的两个交点间的线段的长度;(2)求原点到该图象的距离。7、某校新买了一批桌椅,桌、椅的高度满足一次函数关系,当椅子的高度为50㎝时,桌子的高度为80㎝;当椅子的高度为55㎝时,桌子的高度为85㎝,根据要求,桌子的高度不低于70㎝,不高于100㎝,经测量有一把椅子的高度45㎝,问该椅子是否符合要求?请运用相关知识说明理由。附答案:一、1—5BBCBD,6—10CACBC二、1、(0,6),2、,3、y=3x+2,4、答案不唯一,5、1,6、(-3,5)或(3,3),7、k>0,b<0,8、25,9、m=0,10、3.三、1、y=-2x+3,2、y=4x+6,3、5(单位面积)4、①当x=-1,y=-6;x=5,y=0时解得∴一次②当x=-1,y=0;x=5,y=-6时解得∴一次函数的关系式为y=x-5或y=-x-1;5、(1)y=x;(2)超过5吨时的关系式为y=1.5x-2.5,8>5,∴当x=8时y=1.5×8-2.5=9.5∴该居民应付水费9.5元。6、(1)设一次函数与x轴、y轴的交点分别为A、B(图略)当y=0时由0=-x+12,解得x=5,得A点坐标为(5,0),同理可得B点坐标为(0,12),∴OA=5,OB=12,由勾股定理得AB==13(2)设原点到该图象的距离为OC,∴S△AOB=AB×OC=OA×OB∴13OC=5×12∴OC=7、设一次函数的关系式为y=kx+b,根据题意得42\n初中数学测试题解得∴一次函数的关系式为y=x+30当x=45时y=45+30=75而70<75<100,∴该椅子符合要求。一、填空:(每小题2分,共24分)1、对角线___平行四边形是矩形。2、如图⑴已知O是□ABCD的对角线交点,AC=24,BD=38,AD=14,那么△OBC的周长等于___ABDCO⑴ADBCFE⑷ABDCE⑶ABDCO⑵3、在平行四边形ABCD中,∠C=∠B+∠D,则∠A=___,∠D=___。4、一个平行四边形的周长为70cm,两边的差是10cm,则平行四边形各边长为____cm。5、已知菱形的一条对角线长为12cm,面积为30cm2,则这个菱形的另一条对角线长为__________cm。6、菱形ABCD中,∠A=60o,对角线BD长为7cm,则此菱形周长_____cm。7、如果一个正方形的对角线长为,那么它的面积______。8、如图2矩形ABCD的两条对角线相交于O,∠AOB=60o,AB=8,则矩形对角线的长___。9、如图3,等腰梯形ABCD中,AD∥BC,AB∥DE,BC=8,AB=6,AD=5则△CDE周长___。10、正方形的对称轴有___条11、如图4,BD是□ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需增加的一个条件是______12、要从一张长为40cm,宽为20cm的矩形纸片中,剪出长为18cm,宽为12cm的矩形纸片,最多能剪出____张。二、选择题:(每小题3分,共18分)13、在□ABCD中,∠A:∠B:∠C:∠D的值可以是( )A、1:2:3:4 B、1:2:2:1 C、2:2:1:1 D、2:1:2:114、菱形和矩形一定都具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分 D、对角线互相平分且相等15、下列命题中的假命题是( )A、等腰梯形在同一底边上的两个底角相等B、对角线相等的四边形是等腰梯形C、等腰梯形是轴对称图形D、等腰梯形的对角线相等16、四边形ABCD的对角线AC、BD交于点O,能判定它是正方形的是( )A、AO=OC,OB=OD B、AO=BO=CO=DO,AC⊥BDC、AO=OC,OB=OD,AC⊥BD D、AO=OC=OB=OD42\n初中数学测试题17、给出下列四个命题⑴一组对边平行的四边形是平行四边形 ⑵一条对角线平分一个内角的平行四边形是菱形⑶两条对角线互相垂直的矩形是正方形 ⑷顺次连接等腰梯形四边中点所得四边形是等腰梯形。其中正确命题的个数为( )A、1个 B、2个 C、3个 D、4个18、下列矩形中按虚线剪开后,能拼成平行四边形,又能拼成直角三角形的是( )中点中点中点三、解答题(58分)19、(8分)如图:在□ABCD中,∠BAD的平分线AE交DC于E,若∠DAE=25o,求∠C、∠B的度数。ECDAB20、(8分)已知在梯形ABCD中,AD∥BC,AB=DC,∠D=120o,对角线CA平分∠BCD,且梯形的周长20,求AC。ADBC21、证明题:(8分)如图,△ABC中∠ACB=90o,点D、E分别是AC,AB的中点,点F在BC的延长线上,且∠CDF=∠A。ABDCFE求证:四边形DECF是平行四边形。EADBFC22、如图△ABC中,∠ACB=900,CD平分∠ACB,DE//BC,DF//AC,分别交AC、BC于E,F。求证:四边形DECF是正方形(8分)23、(8分)已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是________试证明:这个多边形是菱形。A42\n初中数学测试题EFCDB八年级数学单元测试答案一、⑴相等;⑵45;⑶∠A=120o,∠D=60o;⑷22.5,12.5;⑸5;⑹28;⑺1;⑻16;⑼15;⑽4;⑾略;⑿3。二、⒀D;⒁C;⒂B;⒃B;⒄B;⒅B19、解:∠BAD=2∠DAE=2×25o=50o (2分)又∵□ABCD ∴∠C=∠BAD=50o (4分)∴AD∥BC∴∠B=180o-∠BAD (6分)ADBC123=180o-50o=130o (8分)20、解:∵AD∥BC ∴∠1=∠2 又∠2=∠3∴∠1=∠3 AD=DC (2分)又AB=DC 得AB=AD=DC=在△ADC中∵∠D=120o ∠1=∠3=又∠BCD=2∠3=60o∴∠B=∠BCD=60o(4分)∠BAD=180o-∠B-∠2=90o ∠2=30o则BC=2AB=2x(6分)AB=4 BC=8 在Rt△ABC中AC= (8分)21、⑴△BCE≌△DCF (1分) 理由:因为四边形ABCD是正方形∴BC=CD,∠BCD=90o∴∠BCE=∠DCF 又CE=CF ∴△BCE≌△DCF (4分)⑵∵CE=CF∴∠CEF=∠CFE ∵∠FCE=90o∴∠CFE=又∵△BCE≌△DCF ∴∠CFD=∠BEC=60o (6分)∴∠EFD=∠CFD-∠CFE=60o-45o=15o (8分)22、证明:∵D、E分别是AC、AB的中点 ∴DE∥BC (1分)∵∠ACB=90o∴CE=AB=AE (3分)∵∠A=∠ECA ∴∠CDF=∠A (4分)∴∠CDF=∠ECA∴DF∥CE(7分)42\n初中数学测试题∴四边形DECF是平行四边形 (8分)23、答条件AE=AF(或AD平分角BAC,等) (3分)证明:∵DE∥AC DF∥AB∴四边形AEDF是平行四边形 (6分)又AE=AF∴四边形AEDF是菱形(8分)七下数学第十章二元一次方程组测试题一、选择题(每题2分,共24分)1.方程x+2y=4的正整数解有()A.1个B.2个C.3个D.0个2.已知与都是方程x+cy=0的解,则c的值为()A.1B.2C.3D.43.若方程组的解是二元一次方程3x-2y=10的解,则b的值为()A.1lB.7C.4D.14.若方程组的解是二元一次方程3x-5y=28的一组解,则的值为()A.3B.2C.7D.65.如果37xxby+7与22-4yb2x的和是单项式,则x、y的值分别为()A.-3、2B.2、-3C.-2、3D.3、-26.若,则x的值为()A.-lB.1C.2D.-27.当x=2时.代数式x3+bx+l的值为6,那么当x=-2时这个式子的值为()A.6B.-4C.5D.18.如图,将正方形ABCD的一角折叠,折痕为AE,∠BAD比∠BAE大48°.设∠BAE和∠BAD的度数分别为x、y,那么x、y所适合的一个方程组是()A.B.C.D.9.已知x、y、z同时满足方程x+3y-5z=0,2x-y-3z=0.则x:y:z的值为.()A.2:l:lB.3:2:1C.1:2:1D.2:3:542\n初中数学测试题10.王林同学两次从盘子中共拿出6只苹果,第一次拿出x只,第二次拿出y只,且每次至少拿出1只,不同的拿法共有()A.3种B.4种C.5种D.6种11.6年前,小虎的年龄是明明的3倍,现在小虎的年龄是明明的2倍,则小虎现在的年龄为()A.12岁B.18岁C.24岁D.30岁12.为确保信息安全,信息需要加密传输,发送方由明文→密文(加密),接收方由密文→明文(解密).已知加密规则为:明文、b、c对应的密文+1、2b+4、3c+9.例如明文1、2、3对应的密文2、8、18.如果接收方收到密文7、18、15,则解密得到的明文为()A.4、5、6B.6、7、2C.2、6、7D.7、2、6二、填空题(每题2分,共20分)13.若方程4x=2y+1,则用含x的代数式表示y=_______________.14.是方程3x-3y=m和5x+y=n的公共解,则m2-n的值为____________.15.方程组的解中x与y的值相等,则k=_____________.16.已知方程组如果不解方程组,那么x-y=_____________.17.如果关于x的方程4x-2m=3x+2和x=2x-3m的解相同,则m=____________.18.已知二元一次方程组的解是则+b=_____________.19.已知s=2x,t=2-x,则用含t的代数式表示s,应该是______________________.20.已知一个梯形的面积为25cm2,高为5cm,它的下底比上底的2倍多1cm,则梯形的上底和下底长分别为____________________.21.三个同学对问题“若方程组的解是求方程组的解.”提出各自的想法·甲说:“这个题目好象条件不够,不能求解.”乙说:“它们的系数有一定的规律,可以试试.”丙说:“可以把第二个方程组的两个方程的两边都除以5,通过换元替换的方法来解决.”参考他们的讨论,你认为这个题目的解应该是:_____________.22.如图,周长为68cm的矩形ABCD是由7个相同的小矩形组合而成,则矩形ABCD的面积为____________.三、解答题(共56分)23.(8分)解下列方程组:(1)(2)24.(6分)已知y=x2+px+q,当x=1时,y=2;当x=-2时,y=2.求当x=-3时y的值.42\n初中数学测试题25.(6分)当k为何值时,方程组中x与y互为相反数,求出方程组的解.26.(7分)已知方程组与方程组有相同的解,求、b的值.27.(5分)已知是方程组的解,求+b+c的值.28.(8分)某蔬菜公司收购到某种蔬菜140吨,准备加工上市销售.该公司的加工能力是:每天可以精加工6吨或粗加工16吨.现计划用15天完成加工任务,该公司应安排几天精加工,几天粗加工?29.(8分)抗洪指挥部的一位驾驶员接到一个防洪的紧急任务,要在限定的时间内把一批抗洪物质从物资局仓库运到水库.这辆车如果按每小时30千米的速度行驶,在限定的时间内赶到水库,还差3千米,他决定以每小时40千米的速度前进,结果比限定时间早到18分钟.限定时间是几小时?物资局仓库离水库有多远?30.(8分)某水果批发市场香蕉的价格如下表:购买香蕉数不超过20千克20千克以上但不超过40千克40千克以上每千克价格6元5元4元张强两次共购买香蕉50千克(第二次多于第一次),共付款264元,请问张强第一次、第二次分别购买香蕉多少千克?参考答案一、1.A2.D3.A4.B5.B6.A7.B8.C9.A10.C11.C12.B42\n初中数学测试题二、13.14.23215.216.-817.218.319.s=-2t+420.3cm、7cm21.22.280cm2三、23.(1)(2)24.625.k=826.=14b=227.+b+c=328.10天精加工,5天粗加工29.限定时间为1.5小时,物资局仓库离水库48千米30.张强第一次购买14千克,第二次购买36千克不等式与不等式组一.选择题。(每题3分,共15分)1.已知,则下列不等式中,不一定正确的是()A.B.C.D.2.不等式的解集是()A.B.C.D.3.三个连续自然数的和不大于12,符合条件的自然数共有()A.1组B.2组C.3组D.4组4.已知三角形的两边,第三边是,且,则的取值范围是()A.B.C.D.5.下列说法中,正确的是()A.如果,那么B.如果,那么C.如果,那么D.如果,那么二.填空题。(每题3分,共15分)1.不等式组的解集是。2.若不等式与的解集相同,则。3.在直角坐标系中,点在第四象限,则的取值范围是。4.若,则(填)5.若代数式的值不小于代数式的值,则的取值范围是。三.解不等式(组),并把解集在数轴上表示出来。(每题10分,共40分)1.2.42\n初中数学测试题3.4.四.解答题。(每题15分,共30分)1.某校为了鼓励在数学竞赛中获奖的学生,准备买若干本课外读物送给他们,如果每人送3本,则还剩8本;如果每人送5本,则最后一人得到的课外读物不足3本,求该校的获奖人数及所买的课外读物的本数?2.要使关于的方程的解在-3与2之间,试求适合条件的的整数值。答案:一.DADBA二.1.2.3.4.5.三.1.2.3.4.四.1.该校获奖人数为6人,所买的课外读物为26本2.m=0,142