初中几何专项练习(含答案)资料

初中几何专项练习(含答案)资料

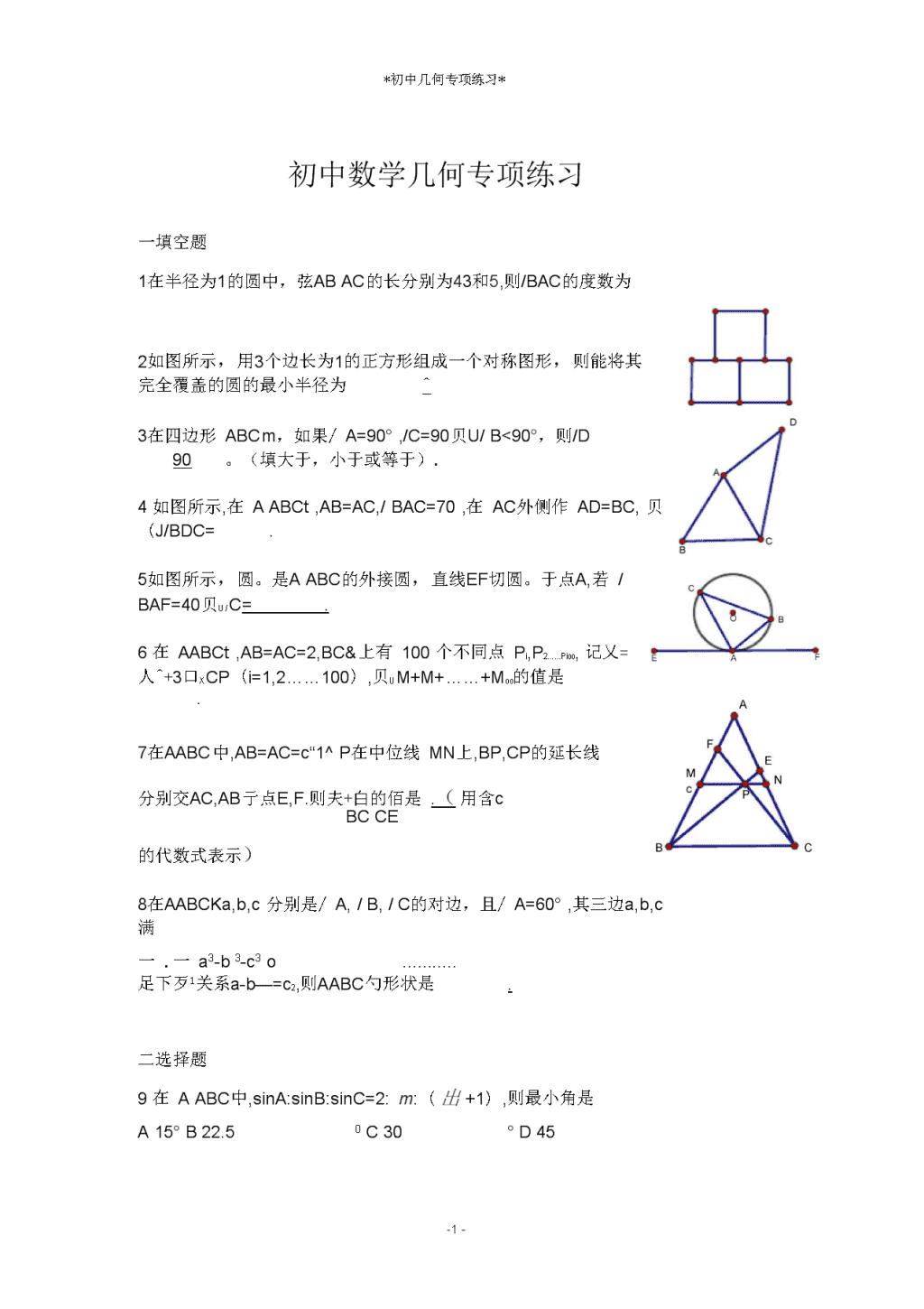
*初中几何专项练习*初中数学几何专项练习一填空题1在半径为1的圆中，弦ABAC的长分别为43和5,则/BAC的度数为2如图所示，用3个边长为1的正方形组成一个对称图形，则能将其完全覆盖的圆的最小半径为^3在四边形ABCm，如果/A=90°,/C=90贝U/B<90°，则/D90。（填大于，小于或等于）.4如图所示,在AABCt,AB=AC,/BAC=70,在AC外侧作AD=BC,贝（J/BDC=.5如图所示，圆。是AABC的外接圆，直线EF切圆。于点A,若/BAF=40贝U/C=.6在AABCt,AB=AC=2,BC&上有100个不同点Pi,P2……Pioo,记乂=人^+3口XCP（i=1,2……100）,贝UM+M+……+Moo的值是.7在AABC中,AB=AC=c“1^P在中位线MN上,BP,CP的延长线分别交AC,AB亍点E,F.则夫+白的佰是.（用含cBCCE的代数式表示）8在AABCKa,b,c分别是/A,/B,/C的对边，且/A=60°,其三边a,b,c满一.一a3-b3-c3o足下歹1关系a-b—=c2,则AABC勺形状是.二选择题9在AABC中,sinA:sinB:sinC=2:m:（出+1）,则最小角是A15°B22.50C30°D45-11-\n*初中几何专项练习*10在AABC中，若a2+b2=c2+ab,则/C的大小为A600B450C35°D22.5-11-\n*初中几何专项练习*则/C的大小为11在AABC中，若(a+b+c)(sinA+sinB-sinC)=3asinB,-11-*初中几何专项练习*A600B45C35D22.5-11-*初中几何专项练习*-11-*初中几何专项练习*12如图所示，在三个等圆上各自有一条劣弧AB,CD,EF,如果劣弧AB+CD=E哪么AB+CDtEF的大小关系是AAB+CD>EFcab+cd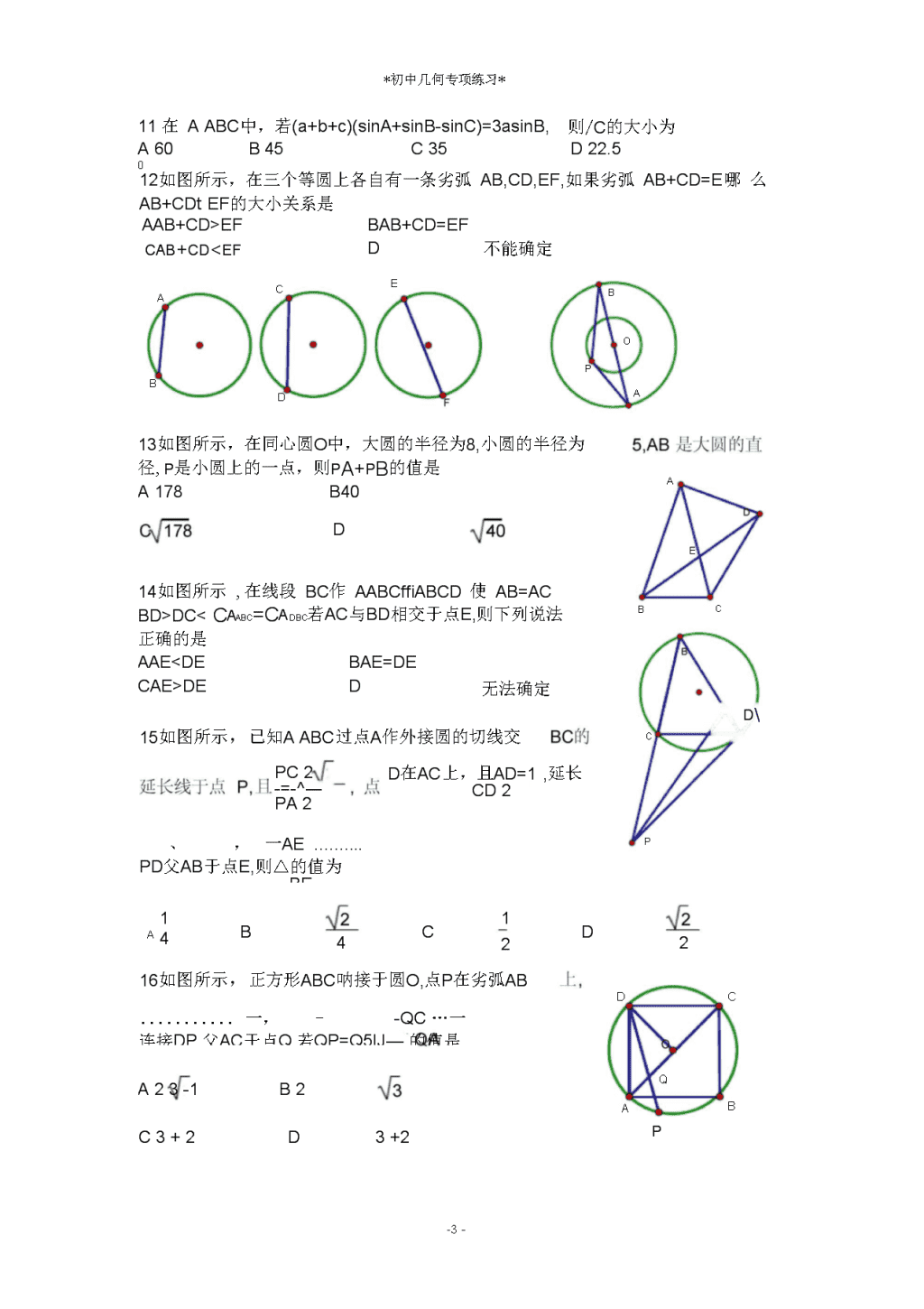DCDE15如图所示，已知AABC过点A作外接圆的切线交16如图所示，正方形ABC呐接于圆O,点P在劣弧AB1A4A23-1一，--QC…一连接DP,父AC于点Q,若QP=Q5IJ—的值是,在线段BC作AABCffiABCD使AB=ACabc=Cadbc若AC与BD相交于点E,则下列说法PC2-=-^―PA213如图所示，在同心圆O中，大圆的半径为8,小圆的半径为径,p是小圆上的一点，则pA+pB的值是A178B40D在AC上，且AD=1,延长CD2d\、，一AEPD父AB于点E,则△的值为BEC3+23+2pD-11-\n*初中几何专项练习*17如图所示，一个六边形有一个外接圆和一个内切圆，并且这两个圆是同心圆则关于这个六边形的形状下列描述最准确的是A正六边形B正方形C普通六边形D对称六边形18如图所示，延长六边形的边AB,CD,EF,两两相交于H,M,N,那么AHMNW六边形ABCDE的面积比是A3:2B2:1C4:3D5:4-11-*初中几何专项练习*-11-*初中几何专项练习*-11-*初中几何专项练习*-11-*初中几何专项练习*三应用题19以。为圆心画大圆，在其直径中，任取一点画小圆（小圆完全在大圆内，且S大圆＞S〃、圆），如图所小，若AB是大圆的弦，且AB与大圆直径平行，且切于小圆，那么阴影部分的面积是多少？（结果可保留n）20在一个平行四边形ABCM，求证:AB2+BC+CD+DA=bD+aC.-11-\n*初中几何专项练习*-11-*初中几何专项练习*21如图所示，在AABC^,AB=AC,E、F分另是ABAC上的点，且有AE=CD若BC=2求EF的最小值。22如图所示,若该圆外接于正方形ABCD,刻劣弧上的一点,设s=pA+pC则S是定值吗？若是求出该PB值,若不是，请说明理由.23如图所示,0为AABC内任意一点，AP,BO,CO的延长线分别交对边于A,Bi,Ci,求证：A0B0C0AA+BB+CC为定值.-11-\n*初中几何专项练习*24如图所示(左)，正方形ABCD勺边长为2,点M是BC上的中点，P是线段MCt的一个动点(至MC点不运动)，以AB为直径作圆O,过点P的切线交AD于点F,切点为E。(1)求四边形CDFPP勺周长(2)请连接OF,OP求证：PF±OP(3)延长DCFP相交于点G连接OE并延长交直线DC于H,如图所示(右)，是否存在点P使AEF8AEHG如果存在，试求此时的BP的长，如果不存在，请说明理由-11-*初中几何专项练习*-11-*初中几何专项练习*-11-*初中几何专项练习*-11-*初中几何专项练习*25如图所示,AB是圆O的直径,BC是其弦，圆0的割线PDELAB于点F,交BC于点G,连接PC,/BACWBCP(1)求证:CP是圆O的切线(2)当/BAC=30,BG=23,CG=4^/3时，求以PD,PE的长度为两根的一元二次方程.(3)若(1)的条件不变，当点C在劣弧AD上运动时，应再具备什么条件可以使结论bG=bfxbo成立？试写出你的猜想，并说明理由.-11-\n*初中几何专项练习*-11-*初中几何专项练习*26-11-*初中几何专项练习*如图，在锐角三角形ABC中，AB上的高CE与AC上的高BD相交于点H,以DE为直径的圆分别交AB、AC于F、G两点，FG与AH相交与点K,已知BC=25,BD=20。BE=7,求AK的长-11-*初中几何专项练习*-11-*初中几何专项练习*27-11-*初中几何专项练习*如图所示，锐角三角形边BC上有两点EF,满足角BAE=HCAF,作FM垂直于AB,FN垂直于AC（M、N为垂足），延长AE交ABC的外接圆于点D,证明四边形AMDN与三角形ABC面积相等-11-\n*初中几何专项练习*-11-*初中几何专项练习*参考答案一选择题115°或7525^2163大于由题得/B+/D=90，因为/B<90,所以/D>904350连接BD,因为AB=AC=AD,以点以/BDC=35540064X100BCDft以点A为圆心,AB长为半径的圆上,所设MP=t,BC=a,所以NP=0.5a-t“、，MPMFNPNE又因为一==BCBFBCCE即上=工但匚」所以工+」=at+°2=31aBFaCE加以BCCE0.5acc8等边A整理得(a-b)(a2+b2-c2+ab)=0当A=B时，AABE等边A.,0001.当a+b-c+ab=0时,cosC=-2,舍去.二选择题9D设sinA:sinB:sinC=2:y]6:(y[3+1)=k,所以cosA=^,贝U/A=45.10A由题得c2=a2+b2-ab=a2+b2-2x(0.5)xab所以cosC=0.5则/C=6011A由题得(a+b+c)(a+b-c)=3ab,口222「a2+b2-c21即a+b-c=ab所以cosC=o.=；2ab2所以/C=60-11-\n*初中几何专项练习*12B13APA2=64+25-2X8X5Xcos/POAPB2=64+25-2X8X5Xcos/(180-POA)因为cos/POA=cos/(180-POA)所以PA2+PB2=2X(64+25)=17814C在BD上取点F,使DF=AC连接AF,AD,所以DB>AC,因为AB+AC=BD+CD=2AC在AABF中,AF>AB-BF=DC又因为/BDA/CAD,所以DC+BF=AC=AB在AADCtAADF中,AC=DFAF>CD所以AE>DE15A16D设半径为r,QO=QP=m,QC=r+m,QA=r-m所以(r-m)(r+m)=mXQD©目交弦定理)得出QDQCr-m3+3所以6=诉=3-3=3+2因为qD=dO+qO得出qD所以(r~~m)2=r2+n2m=-r、m’317A18A三应用题1918n将小圆平移到大圆的圆心。上，在AB中点取一点C,连接OC,由垂径定理得贝UOCLAB,且AC=6,在RtAOAC或AOBC加,设小圆半径OC=a因为AC=6,所以由勾股定理可得OA=36+a21_1_122122所以s阴影=2s大圆-2s小圆=2ii(oa-oc)=2n(36+a-a)=18n20证明如下在ABADP,因为。是BD的重点，由中线定理得AD2+AB=2(AC2+BO)所以AE2+AB=2((2AO)2+2(BO)2)故AC2+BD=2(AB2+AD)所以A寸+BC+CD+DA=BD+AC.211设AE=kAB=AC=a则AF=BE=a-x0BCa-11-\n*初中几何专项练习*所以2a>2a>1故4-2>0a44a--a所以当x=———2(4a2)2i=-时EFa2a最小值=22a2+1=1-11-*初中几何专项练习*-11-*初中几何专项练习*22是定值,且SR2延长PC至M,使CM=PAg接MB所以AMC空APAB故/PBAWMBC/PBM=ABC=90,BP=BM所以APBM^等腰A所以PM=PC+CM2PB即PA+PC=2PBPA+PC—所以s==q2(止值)PB123证明如下已知AO,AA为底边的AAOB,AABA的高相等SAAOBAO日抻SAAOCAO所以SAABA=AAi同理SAACA=AAi一二SAAOB+aAOC=SAAOB+SAOCAAiSAABA+SAACASAABC同理COSAAOB+SAOCCCi=SAABCBOSAAOB+&AOCBBi=SAABCAO+B0+C0=2xSAABC=2AABBCCSAABC24(1)6(2)证明如下连接OE所以OELPF再证明AAOF^AEOF得/AOFWEOF同理/BOP=EOP所以/EOF廿EOP=9O所以/FOP=9O所以OF!OP(3)存在当AEOCAEHG寸，/BOP=60所以BP=/325(1)证明略(2)x2-103x+48=0证明ACP@正A,得PC=CG=43-11-\n*初中几何专项练习*因为pC=PEXPE=48BC=673所以AB=12FD=3/3EG=473所以PD=23PD+PE=103即可得二元一次方程x2-103x+48=0(3)当G为BC的中点,OG±BC,OG/AC或/BOG=BAC寸(凡是能证明ABF中ABGO勺条件皆可)268.64、『…ADDBAB证明AAD改AAEC所以T；-=而=T7kAECEAC因为BC=25BD=20BE=7所以CD=15CE=24AD_5AE+75AE=6AD+15=6所以AD=15AE=18DE=15/DFE=90故AF=9因为GFEDft圆，所以DEBCft圆，所以/AFGWADEWABCGF/CBAKAF延长AH父BC于P,则布=~APAB又因为H为AABC的垂心一一，AFXAP可得BA=BC所以AP=CE=24AK=AB=8.6427证明如下连接MN,BD贝UAMFNH点共圆所以/AMN=AFN所以/AMN+BAE=90_1_S四边形AMD=2ADXMN因为/CAF=/DAB,/ACFWADB所以AAFOAABD则ABXAC=ADCAF因为AF是过AMFI®点的圆的直径所以AFsinZBAC=MN1..所以Saabc=2ABXACXsin/BAC1一一-八ADxAFXsin/BAC212ADXMN=S四边形AMDN所以SaabuS四边形AMDN-11-