实验参考答案

实验参考答案

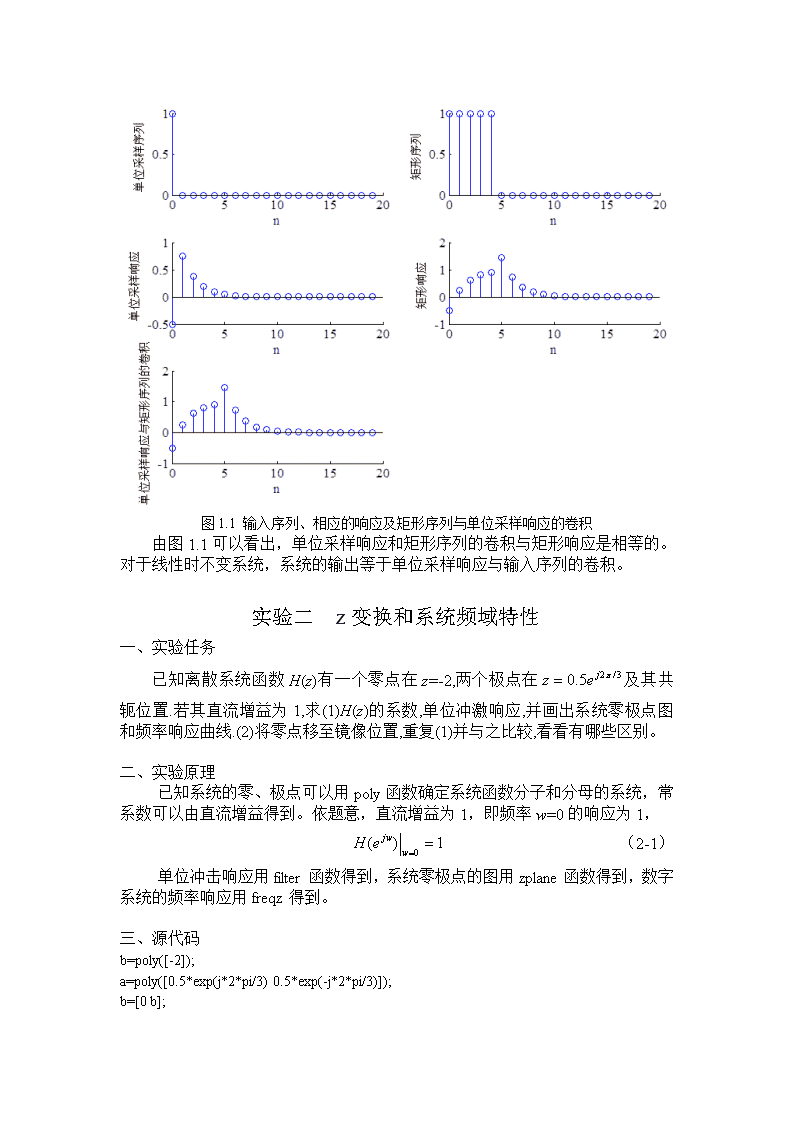
实验一离散时间信号与系统一、实验任务用filter函数计算一全通系统(z-1-0.5)/(1-0.5z-1)的单位采样响应h(n)，矩形序列R5(n)的响应;比较该响应与R5(n)*h(n)的结果.二、实验原理线性时不变系统的响应用filter函数得到:y=filter(b,a,x)x为输入序列，b和a分别为系统函数分子和分母的系数，返回的y为输出序列。卷积用conv函数计算。三、源代码n=0:19;x1=[1,zeros(1,19)];x2=[ones(1,5)zeros(1,15)];subplot(3,2,1);stem(n,x1);xlabel('n');ylabel('');subplot(3,2,2);stem(n,x2);xlabel('n');ylabel('R5(n)');b=[-0.51];a=[1-0.5];y1=filter(b,a,x1);y2=filter(b,a,x2);subplot(3,2,3);stem(n,y1);xlabel('n');ylabel('单位采样响应');subplot(3,2,4);stem(n,y2);xlabel('n');ylabel('矩形响应');y=conv(x2,y1);y3=y(1:20);subplot(3,2,5);stem(n,y3);xlabel('n');ylabel('单位采样响应与矩形序列的卷积');四、结果与讨论n图1.1输入序列、相应的响应及矩形序列与单位采样响应的卷积由图1.1可以看出，单位采样响应和矩形序列的卷积与矩形响应是相等的。对于线性时不变系统，系统的输出等于单位采样响应与输入序列的卷积。实验二z变换和系统频域特性一、实验任务已知离散系统函数H(z)有一个零点在z=-2,两个极点在及其共轭位置.若其直流增益为1,求(1)H(z)的系数,单位冲激响应,并画出系统零极点图和频率响应曲线.(2)将零点移至镜像位置,重复(1)并与之比较,看看有哪些区别。二、实验原理已知系统的零、极点可以用poly函数确定系统函数分子和分母的系统，常系数可以由直流增益得到。依题意，直流增益为1，即频率w=0的响应为1，（2-1）单位冲击响应用filter函数得到，系统零极点的图用zplane函数得到，数字系统的频率响应用freqz得到。三、源代码b=poly([-2]);a=poly([0.5*exp(j*2*pi/3)0.5*exp(-j*2*pi/3)]);b=[0b];nK=1/(sum(b)/sum(a));%直流增益为1,求出常系数b=b*K;subplot(2,2,1);zplane(b,a);xlabel('Realpart');ylabel('Imaginarypart');gridon;%根据系统函数返回零极点图N=20;x=[1zeros(1,N-1)];n=0:N-1;subplot(2,2,2);stem(n,filter(b,a,x));xlabel('n');ylabel('h1(n)');gridon;%根据系统函数返回单位冲激响应(离散的)[H,w]=freqz(b,a,N);%根据系统函数返回0~pi间等间隔的N个频率w相应的频率响应Hsubplot(2,2,3);plot(w,abs(H));xlabel('w');ylabel('|H1(exp(jw))|');gridon;subplot(2,2,4);plot(w,angle(H));xlabel('w');ylabel('arg(H1(exp(jw)))');gridon;figure;b=poly([-0.5]);a=poly([0.5*exp(j*2*pi/3)0.5*exp(-j*2*pi/3)]);b=[0b];K=1/(sum(b)/sum(a));%直流增益为1b=b*K;subplot(2,2,1);zplane(b,a);xlabel('Realpart');ylabel('Imaginarypart');gridon;%根据系统函数返回零极点图N=20;x=[1zeros(1,N-1)];n=0:N-1;subplot(2,2,2);stem(n,filter(b,a,x));xlabel('n');ylabel('h1(n)');gridon;%根据系统函数返回单位冲激响应(离散的)[H,w]=freqz(b,a,N);%根据系统函数返回0~2pi间等间隔的N个频率w相应的频率响应Hsubplot(2,2,3);plot(w,abs(H));xlabel('w');ylabel('|H1(exp(jw))|');gridon;subplot(2,2,4);plot(w,angle(H));xlabel('w');ylabel('arg(H1(exp(jw)))');gridon;四、结果与讨论n图2.1零点在z=-2的零极点图，单位采样响应，幅频响应和相频响应图2.1和图2.2分别为系统零点在z=-2和镜像位置z=-0.5，两个极点在及其共轭位置的零极点图，单位采样响应，幅频响应和相频响应。比较可见，将零点由单位圆外移到单位圆内的镜像位置，由非最小相位系统变成了最小相位系统，并没有改变系统的幅频响应，而单位采样响应和相频响应都有变化。图1和图2的h(0)都等于0，图1的h(1)=0.5833，图2的h(1)=1.1667，可见最小相位系统的单位采样响应序列的能量集中在n=0附近，从相频响应曲线可以看出，最小相位系统的相频响应曲线的斜率较小，因此最小相位系统具有较小的群延迟。n图2.2零点在z=-0.5的零极点图，单位采样响应，幅频响应和相频响应实验三DFT与FFT一、实验任务1.有一调幅信号（3-1）用DFT做频谱分析，画出幅频特性。(1)抽样频率fs=3kHz，抽样数据N=512点；(2)抽样频率fs=2kHz，抽样数据N=512点；(3)抽样频率fs=1kHz，抽样数据N=512点；(4)抽样频率fs=3kHz，抽样数据N=60点；讨论fs与N满足什么条件才能使抽样信号能分辨所有的频率分量。讨论fs与N满足什么条件才能使抽样信号能分辨所有的频率分量。2．已知序列x(n)=[1,2,2],y(n)=[1,2,3,4]，求x(n)与y(n)的4点圆周卷积。二、实验原理1.给出了一个模拟信号，要求用DFT做频谱分析。首先对模拟信号进行抽样，令t=nT，其中T为抽样时间间隔，为抽样频率的倒数，即T=1/fs。n=0,1,2,…,N-1，N为抽样点数。然后对抽样得到的N个数据用fft函数进行离散傅里叶变化，得到信号的频谱。2.计算圆周卷积有两种方法。方法一，先用conv函数求出x与y的线性卷积，再进行周期沿拓；方法二，对x序列补零，使x与y序列的长度一样，分别做4n点DFT，得到X(k)与Y(k)，那么x序列与y序列的4点圆周卷积等于IDFT[X(k)Y(k)]。三、源代码1.N1=512;n1=0:N1-1;fs1=3000;x1=[1+cos(2*pi*100*n1/fs1)].*cos(2*pi*600*n1/fs1);X1=fft(x1);subplot(4,1,1);stem(n1,abs(X1));N2=512;n2=0:N2-1;fs2=2000;x2=[1+cos(2*pi*100*n2/fs2)].*cos(2*pi*600*n2/fs2);X2=fft(x2);subplot(4,1,2);stem(n2,abs(X2));N3=512;n3=0:N3-1;fs3=1000;x3=[1+cos(2*pi*100*n3/fs3)].*cos(2*pi*600*n3/fs3);X3=fft(x3);subplot(4,1,3);stem(n3,abs(X3));N4=20;n4=0:N4-1;fs4=3000;x4=[1+cos(2*pi*100*n4/fs1)].*cos(2*pi*600*n4/fs1);X4=fft(x4);subplot(4,1,4);stem(n4,abs(X4));2.%方法一x=[122];y=[1,2,3,4];N=4;zl=conv(x,y);z=zeros(1,N);fori=1:Nfork=i:N:length(zl)z(i)=z(i)+zl(k);endendz%方法二x=[122];ny=[1,2,3,4];X=fft([x0]);Y=fft(y);z=ifft(X.*Y)四、结果与讨论1．图3.14种抽样方法得到的频谱对模拟信号的表达式化简（3-2）可以看出模拟信号的频谱在频率为500Hz，600Hz，700Hz有峰值，其他频率信号的幅度为零。频谱分析如图3.1所示，可以看出（1）和（2）能清晰的分辨出这三个峰值，而（3）的频谱在k=250出现了混跌现象，图(4)的抽样点数太少了，峰值很模糊。根据奶奎斯特抽样定理，抽样频率应大于信号最高频率的两倍，因此抽样频率必须大于1400Hz，抽样点数N≥fs/F0，F0为频率分辨率，（4）的抽样频率为3kHz，F0=100Hz，因此抽样点数至少为30点，因此（1）和（2）这两种抽样条件能使抽样信号能分辨所有的频率分量。2．方法一z=1512914方法二z=n1512914可见，先求线性卷积再做周期沿拓和先算两序列的DFT再求积最后求IDFT这两种方法都能得到x序列与y序列的4点圆周卷积，计算的结果是一致的。从程序和计算量角度来看，第二种方法比较简单。实验四IIR滤波器的设计一、实验任务设计一IIR数字带通滤波器，给定指标为（1）200Hz600Hz，衰减>20dB，（3）抽样频率fs=2kHz。（1）用巴特沃斯滤波器，冲击响应不变法；（2）用巴特沃斯滤波器，双线性变换法；（3）用切比雪夫滤波器，冲击响应不变法；（4）用切比雪夫滤波器，双线性变换法。二、实验原理IIR滤波器的设计MATLAB中有各种函数可以使用，设计巴特沃斯滤波器用buttord和butter这两个函数，设计切贝雪夫滤波器用cheb1ord和cheby1这两个函数。题目给出的是模拟技术指标，先转换成数字技术指标，，，，，用冲击响应不变法，先用线性关系转换成模拟滤波器的技术指标设计模拟滤波器，再用impinvar函数转换成数字滤波器；用双线性变换法，先用非线性关系转换成模拟滤波器的技术指标设计模拟滤波器，再用bilinear函数转换成数字滤波器，或直接设计数字滤波器。三、源代码fs=2000;Wc=[2*pi*2002*pi*400];Wst=[2*pi*100,2*pi*600];Rp=2;Rst=20;wc=Wc/fs;wst=Wst/fs;[N,Wn]=buttord(Wc,Wst,Rp,Rst,'s');[B,A]=butter(N,Wn,'s');[b,a]=impinvar(B,A,fs);[h1,w1]=freqz(b,a,256);[N,Wn]=buttord(wc/pi,wst/pi,Rp,Rst);[B,A]=butter(N,Wn);[h2,w2]=freqz(B,A,256);[N,Wn]=cheb1ord(Wc,Wst,Rp,Rst,'s');[B,A]=cheby1(N,Rp,Wn,'s');[b,a]=impinvar(B,A,fs);[h3,w3]=freqz(b,a,256);[N,Wn]=cheb1ord(wc/pi,wst/pi,Rp,Rst);[B,A]=cheby1(N,Rp,Wn);n[h4,w4]=freqz(B,A,256);x=[wc/pi,wst/pi];y=[-Rp,-Rp,-Rst,-Rst];plot(w1/pi,20*log10(abs(h1)),'+',w2/pi,20*log10(abs(h2)),'-',w3/pi,20*log10(abs(h3)),'-.',w4/pi,20*log10(abs(h4)),'.',x,y,'*');grid;xlabel('finpi');ylabel('gainindb');axis([0,1,-50,10]);legend('巴特沃斯，冲击响应不变法','巴特沃斯，双线性变换法','切比雪夫，冲击响应不变法','切比雪夫，双线性变换法');四、结果与讨论图4.14种方法得到的滤波器的幅频响应由图4.1可以看出，设计的4种滤波器都满足题目要求的技术指标。巴特沃斯滤波器在通带没有出现波纹，而切贝雪夫滤波器在通带出现波纹；双线性变换法实现模拟滤波器到数字滤波器的映射不出现混叠现象，而冲击响应不变法实现该转换高频部分有混叠现象，因此，在高频阻带，冲击响应不变法设计的滤波器的幅频响应曲线会往上翘。实验五FIR滤波器的设计一、实验任务1.利用窗函数法设计一个线性相位低通FIR数字滤波器，wp=0.4pi，wst=0.6pi，阻带最小衰减-50dB。2.利用频率抽样法，设计一个低通FIR数字滤波器，wc=0.5pi，抽样点数为N=33，要求滤波器具有线性相位。(1)增加一点过渡带进行优化，过渡带抽样点值为0.5；(2)增加抽样点数至N=65，加两点过渡带优化，过渡带抽样点值为0.5886，0.1065。n二、实验原理1.根据题目给出的阻带最小衰减50dB确定选择的窗函数为海明窗。窗函数的长度由过渡带的宽度确定，(5-1)得到窗函数的长度N=33，再用fir1函数返回系统函数。2.先得到理想滤波器的频率响应，再对理想滤波器的频率响应进行抽样，抽样的点作IDFT就得到了所要设计滤波器的单位采样相应。三、源代码1.wp=0.4*pi;wst=0.6*pi;wc=(wp+wst)/2;N=ceil(6.6*pi/(wst-wp));b=fir1(N-1,wc/pi,hamming(N));[h,w]=freqz(b,1,500);plot(w/pi,20*log10(abs(h)),'-');ylabel('20log(|H|)');xlabel('w/pi');grid;axis([01-10010]);2.N=33;absH=[ones(1,9),zeros(1,16),ones(1,8)];%理想低通滤波器的频率抽样点的幅度。n=0:N-1;angH=-2*pi/N*n*(N-1)/2;%理想低通滤波器的频率抽样点的相角。H=absH.*exp(j*angH);%理想低通滤波器的频率抽样点。b=ifft(H,N);%所设计滤波器的单位抽样响应。[H1,w]=freqz(b,1,500);%加一点过渡带优化|H(9)|=0.5N=33;absH=[ones(1,9),zeros(1,16),ones(1,8)];%理想低通滤波器的频率抽样点的幅度。absH(10)=0.5;absH(25)=0.5;n=0:N-1;angH=-2*pi/N*n*(N-1)/2;%理想低通滤波器的频率抽样点的相角。H=absH.*exp(j*angH);%理想低通滤波器的频率抽样点。b=ifft(H,N);%所设计滤波器的单位抽样响应。[H2,w]=freqz(b,1,500);%增加抽样点数至N=65,加两点过渡带优化N=65;absH=[ones(1,17),zeros(1,32),ones(1,16)];%理想低通滤波器的频率抽样点的幅度。absH(18)=0.5886;absH(19)=0.1065;absH(48)=0.1065;absH(49)=0.5886;n=0:N-1;angH=-2*pi/N*n*(N-1)/2;%理想低通滤波器的频率抽样点的相角。H=absH.*exp(j*angH);%理想低通滤波器的频率抽样点。b=ifft(H,N);%所设计滤波器的单位抽样响应。n[H3,w]=freqz(b,1,500);plot(w/pi,20*log10(abs(H1)),'-',w/pi,20*log10(abs(H2)),'+',w/pi,20*log10(abs(H3)),'-.');ylabel('20log|H|');xlabel('w/pi');grid;legend('N=33','N=33优化','N=65优化');axis([01-10010]);四、结果与讨论图5.1窗函数法设计的滤波器的幅频响应图5.2频率采样法设计的滤波器的幅频响应图5.1为窗函数法设计的滤波器的幅频响应，可以看出，过渡带在0.5π附近，在0.6π的衰减达到了50dB，满足题目的要求。图5.2为n频率采样法设计的滤波器的幅频响应，蓝色的点是没有优化的，绿色的点加了一点过渡带值为0.5的优化，红色的点为增加抽样点数至65，并加了两点过渡带的优化。可以看出增加一点过渡带优化，阻带的波纹明显减小，但过渡带变宽了。增加两点过渡带进行优化，阻带最小衰减更小，增大N可以减小过渡带的宽度。