- 2022-04-07 发布 |
- 37.5 KB |
- 6页


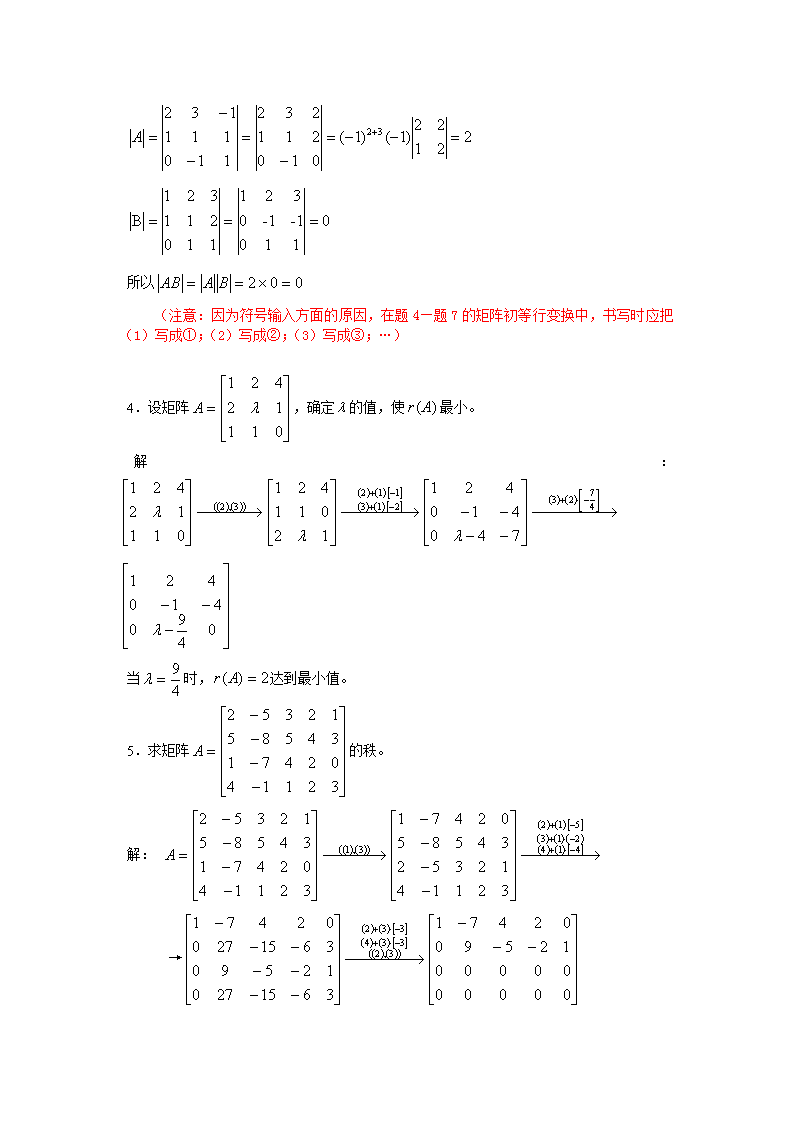
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
经济学基础形形考作业3参考答案
《经济数学基础》形成性考核册(三)(一)填空题1.设矩阵,则的元素.答案:32.设均为3阶矩阵,且,则=.答案:3.设均为阶矩阵,则等式成立的充分必要条件是.答案:4.设均为阶矩阵,可逆,则矩阵的解.答案:5.设矩阵,则.答案:(二)单项选择题1.以下结论或等式正确的是(C).A.若均为零矩阵,则有B.若,且,则C.对角矩阵是对称矩阵D.若,则2.设为矩阵,为矩阵,且乘积矩阵有意义,则为(A)矩阵.A.B.C.D.3.设均为阶可逆矩阵,则下列等式成立的是( C).`A.,B.C.D.4.下列矩阵可逆的是(A).nA.B.C.D.5.矩阵的秩是(B).A.0B.1C.2D.3三、解答题1.计算(1)=(2)(3)=2.计算解=3.设矩阵,求。解因为n所以(注意:因为符号输入方面的原因,在题4—题7的矩阵初等行变换中,书写时应把(1)写成①;(2)写成②;(3)写成③;…)4.设矩阵,确定的值,使最小。解:当时,达到最小值。5.求矩阵的秩。解:→n∴。6.求下列矩阵的逆矩阵:(1)解:∴(2)A=.解:→→∴A-1=7.设矩阵,求解矩阵方程.n解:∴∴=四、证明题1.试证:若都与可交换,则,也与可交换。证:∵,∴即也与可交换。即也与可交换.2.试证:对于任意方阵,,是对称矩阵。证:∵∴是对称矩阵。∵=∴是对称矩阵。∵∴是对称矩阵.3.设均为阶对称矩阵,则对称的充分必要条件是:。证:必要性:∵,若是对称矩阵,即而因此n充分性:若,则∴是对称矩阵.4.设为阶对称矩阵,为阶可逆矩阵,且,证明是对称矩阵。证:∵∴是对称矩阵.证毕.查看更多