圆の解答题答案

圆の解答题答案

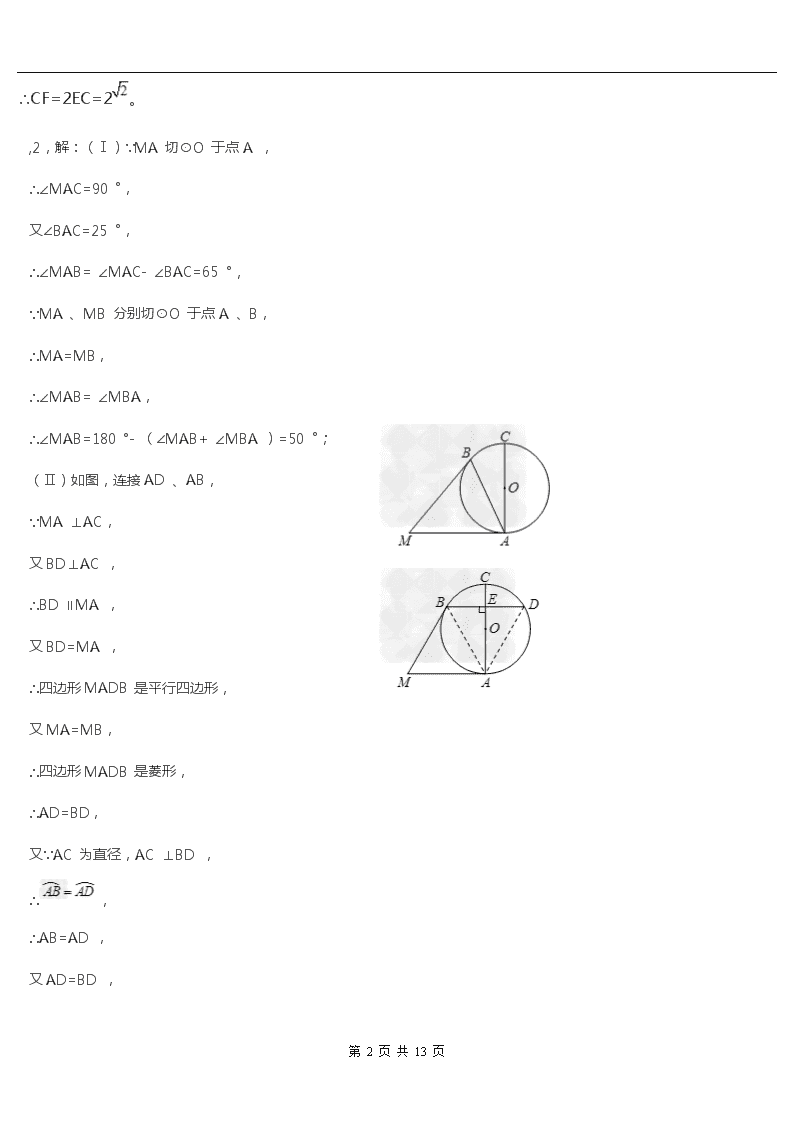
圆の解答题答案直线与圆1，解：（1）∵⊙D与AB相切于点A，∴AB⊥AD，∵AD∥BC，DE⊥BC，∴DE⊥AD，∴∠DAB=∠ADE=∠DEB=90°，∴四边形ABED为矩形；（2）∵四边形ABED为矩形，∴DE=AB=4，∵DC=DA，∴点C在⊙D上，∵D为圆心，DE⊥BC，∴CF=2EC，∵，设AD=3k（k＞0）则BC=4k，∴BE=3k，EC=BC-BE=4k-3k=k，DC=AD=3k，由勾股定理得DE2+EC2=DC2，即42+k2=（3k）2，∴k2=2，∵k＞0，∴k=，第13页共13页n∴CF=2EC=2。,2，解：（Ⅰ）∵MA切⊙O于点A， ∴∠MAC=90°，又∠BAC=25°， ∴∠MAB=∠MAC-∠BAC=65°， ∵MA、MB分别切⊙O于点A、B， ∴MA=MB， ∴∠MAB=∠MBA， ∴∠MAB=180°-（∠MAB+∠MBA）=50°； （Ⅱ）如图，连接AD、AB， ∵MA⊥AC，又BD⊥AC， ∴BD∥MA，又BD=MA， ∴四边形MADB是平行四边形，又MA=MB， ∴四边形MADB是菱形， ∴AD=BD，又∵AC为直径，AC⊥BD， ∴， ∴AB=AD，又AD=BD， 第13页共13页n∴AB=AD=BD， ∴△ABD是等边三角形， ∴∠D=60°， ∴在菱形MADB中，∠AMB=∠D=60°。,3，解：（1）连接OE，        ∵AM、DE是⊙O的切线，OA、OE是⊙O的半径，∴∠ADO=∠EDO，∠DAO=∠DEO=90°， ∴∠AOD=∠EOD=∠AOE， ∵∠ABE=∠AOE∴∠AOD=∠ABE，∴OD∥BE；（2）由（1）得：∠AOD=∠EOD=∠AOE，            同理，有：∠BOC=∠EOC=∠BOE            ∴∠AOD+∠EOD+∠BOC+∠EOC=180°            ∴∠EOD+∠EOC=90°，            ∴△DOC是直角三角形，            ∴CD=（cm）。第13页共13页n4，（1）证明：过O点作OE⊥CD，垂足为E，∵AC是切线，∴OA⊥AC，∵CO平分∠ACD，OE⊥CD，∴OA=OE，∴CD是⊙O的切线；（2）解：过C点作CF⊥BD，垂足为E，∵AC，CD，BD都是切线，∴AC=CE=2，BD=DE=3，∴CD=CE+DE=5，∵∠CAB=∠ABD=∠CFB=90°，∴四边形ABFC是矩形，∴BF=AC=2，DF=BD﹣BF=1，在Rt△CDF中，CF2=CD2﹣DF2=52﹣12=24，∴AB=CF=2。5，（1）证明：∵点A、B在⊙上      ∴OB=OA                 ∴∠OBA=∠ OAB                ∵∠CAD=∠CDA=∠BDO                 ∴∠CAD+∠OAB=∠BDO+∠OBA                 ∵OB⊥OC        ∴∠CAD+∠OAB=90°        ∴∠OAC=90°,  ∴AC是⊙O的切线（2）解:设AC的长为x第13页共13页n∵∠CAD=∠CDA∴CD长为x由（1）知OA⊥AC∴在Rt△OAC中，OA2+AC2=OC2  即52+x2=(1+x)2∴=12，  即线段AC长为12圆心角圆周角1，解：连接BD                          ∵AB⊙O是直径                             ∴BD  ⊥AD                            又∵CF⊥AD∴BD∥CF ∴∠BDC=∠C  又∵∠BDC=∠BOC∴∠C=∠BOC∵AB⊥CD∴∠C=30°∴∠ADC＝60°。2，证明：（1）∵OD⊥AC，OD为半径，∴，第13页共13页n∴∠CBD=∠ABD，∴BD平分∠ABC；（2）∵OB=OD，∴∠OBD=∠ODB=30°，∴∠AOD=∠OBD+∠ODB=30°+30°=60°，又∵OD⊥AC于E，∴∠OEA=90°，∴∠A=180°﹣∠OEA﹣∠AOD=180°﹣90°﹣60°=30°，又∵AB为⊙O的直径，∴∠ACB＝90°，则在Rt△ACB中，BC=AB，∵OD=AB，∴BC=OD．3，解：（1）∵∠ABC与∠D都是弧AC所对的圆周角，∴∠ABC=∠D=60°； （2）∵AB是⊙O的直径，∴∠ACB=90°．∴∠BAC=30°，∴∠BAE=∠BAC+∠EAC=30°+60°=90°，即BA⊥AE，∴AE是⊙O的切线；（3）如图，连接OC，∴OB=OC，∠ABC=60°，∴△OBC是等边三角形，∵OB=BC=4，∠BOC=60°，第13页共13页n∴∠AOC=120°，∴劣弧AC的长为．垂直于直径的弦1，解：过点O作OD⊥AB， ∵AB=12， ∴AD=AB=×12=6， ∵相邻两条平行线之间的距离均为4， ∴OD=8， 在Rt△AOD中， ∵AD=6，OD=8， ∴OA=，答：⊙O的半径为：10。2，解：（1）∵∠APD=∠C+∠CAB， ∴∠C=65°﹣40°=25°， ∴∠B=∠C=25°； （2）作OE⊥BD于E， 第13页共13页n则DE=BE， 又∵AO=BO， ∴，圆心O到BD的距离为3。3，解：（1）四个不同类型的正确结论分别为：∠ACB=90°；BE=CE；=；OD∥AC；（2）∵OD⊥BC，BE=4，∴BE=CE=4，即BC=2BE=8，∵AB为圆O的直径，∴∠ACB=90°，在Rt△ABC中，AC=6，BC=8，根据勾股定理得：AB=10，∴OB=5，在Rt△OBE中，OB=5，BE=4，根据勾股定理得：OE=3，则ED=OD﹣OE=5﹣3=2．中考中的圆2013年解答： 解：（1）AF为圆O的切线，理由为：连接OC，∵PC为圆O切线，∴CP⊥OC，∴∠OCP=90°，∵OF∥BC，第13页共13页n∴∠AOF=∠B，∠COF=∠OCB，∵OC=OB，∴∠OCB=∠B，∴∠AOF=∠COF，∵在△AOF和△COF中， ，∴△AOF≌△COF（SAS），∴∠OAF=∠OCF=90°，则AF为圆O的切线；（2）∵△AOF≌△COF，∴∠AOF=∠COF，∵OA=OC，∴E为AC中点，即AE=CE=AC，OE⊥AC，∵OA⊥AF，∴在Rt△AOF中，OA=4，AF=3，根据勾股定理得：OF=5，∵S△AOF=•OA•AF=•OF•AE，∴AE=，则AC=2AE=．2012年2.（1）证明：∵AB是⊙O的直径∴∠ADB=90°即∠ADC+∠CDB=90°∵∠ADC=∠ABC,∠CBF=∠CDB第13页共13页n∴∠ABC+∠CBF=90°即∠ABF=90°┅┅┅┅┅┅┅┅┅┅┅┅┅2分∴AB⊥EF∴EF是⊙O的切线┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅5分2）解：作BG⊥CD，垂足是G┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅6分在Rt△ABD中∵AB=10,sin∠DAB=又∵sin∠DAB=∴BD=6∵C是弧AB的中点∴∠ADC=∠CDB=45°∴BG=DG=BDsin45°=┅┅┅┅┅┅┅┅┅┅┅┅9分∵∠DAB=∠DCB∴tan∠DCB=∴CG=∴CD=CG+DG=┅┅┅┅┅┅┅┅┅┅┅┅┅11分∴┅┅┅┅┅┅┅┅12分2011年22.(1)证明方法一：连结OC、BC，∵　CD垂直平分OB，∴　OC＝BC.∵　OB＝OC，∴　OB＝OC＝BC.∴　△OCB是等边三角形.∴　∠BOC＝60°.∵　∠CFO＝30°，∴　∠OCE＝90°.∴　OC⊥CF.∵　OC是⊙O的半径，∴　CF是⊙O的切线.第13页共13页n证明方法二：连结OC，∵　CD垂直平分OB，∴　OE＝OB，∠CEO＝90°.∵　OB＝OC，∴　OE＝OC，在Rt△COE中sin∠ECO＝＝.∴　∠ECO＝30°.∴　∠EOC＝60°.∵　∠CFO＝30°，∴　∠OCE＝90°.∵　OC是⊙O的半径，∴　CF是⊙O的切线．(2)连结OD，由(1)可得∠COF＝60°，由圆的轴对称性可得∠EOD＝60°，∴　∠DOA＝120°.∵　OM⊥AD，OA＝OD，∴　∠DOM＝60°.在Rt△COE中CE＝，∠ECO＝30°，cos∠ECO＝，∴　OC＝2.∴　S扇形OND＝＝π.∴　S△OMD＝OM·DM＝.∴　S阴影＝S扇形OND－S△OMD＝π－.2010年(1)解：(法一)：过点O作OG⊥ND于点G∴∠OGD=90°∵四边形ABCD是矩形,∴∠C=90°由翻折得∠N=∠C=90°=∠OGD…………1分∴OG∥BN∵∠NBD=30°∴∠GOD=30°…………3分在Rt△OGD中，cos30°=,OD=3∴OG=…………5分(法二)：过点O作OG⊥ND于点G第13页共13页n则DG=NG…………1分∵OB=OD∴OG是△BDN的中位线∴OG=BN∵四边形ABCD是矩形,∠C=90°∴BD是⊙O直径∵OD=3∴BD=6…………3分在Rt△BND中，cos30°=∴BN=∴OG=…………5分(2)相切.证明：连接OA交BN与H.∵∠DBN=30°,由翻折得∠DBC=∠DBN=30°.∵∠ABC=90°,∴∠ABO=60°.…………1分∵OA=OB,∴△ABO是等边三角形.…………3分∴∠AOB=60°.∴∠BHO=90°.又∵EF∥BN,∴∠FAH=90°.∴ＯA⊥EF.∴EF与⊙O相切.…………5分2009年直线与半圆相切．1分证明：法一：连接，作于点．OABEDC第22题图F∵，∴．2分∵．3分∴，∴．6分∵，∴．7分∴，8分∴，∴∴直线与半圆相切．10分法二：连接，作于点，作于点．∵，∴．第13页共13页n在中，3分∵，，∴四边形是矩形，∴．∵，，5分在中，．∵，∴8分∴．∴直线与半圆相切．10分第13页共13页