2012年四川省达州中考数学试卷及答案

2012年四川省达州中考数学试卷及答案

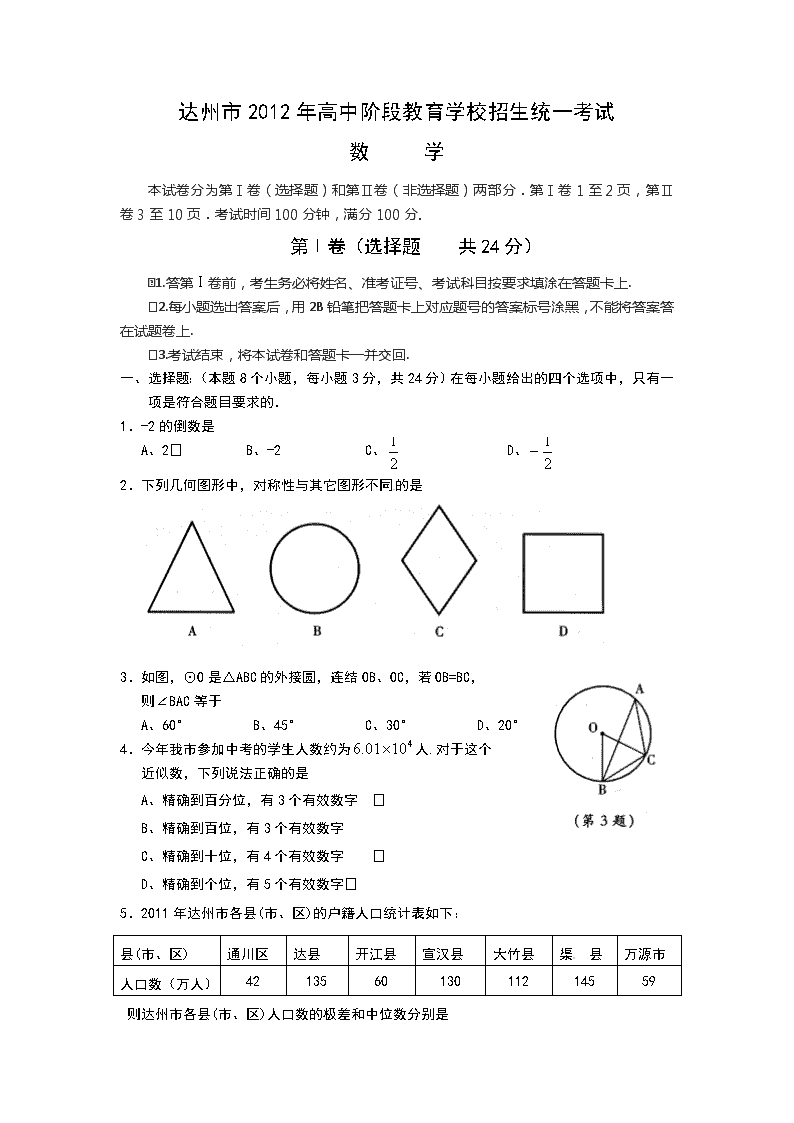
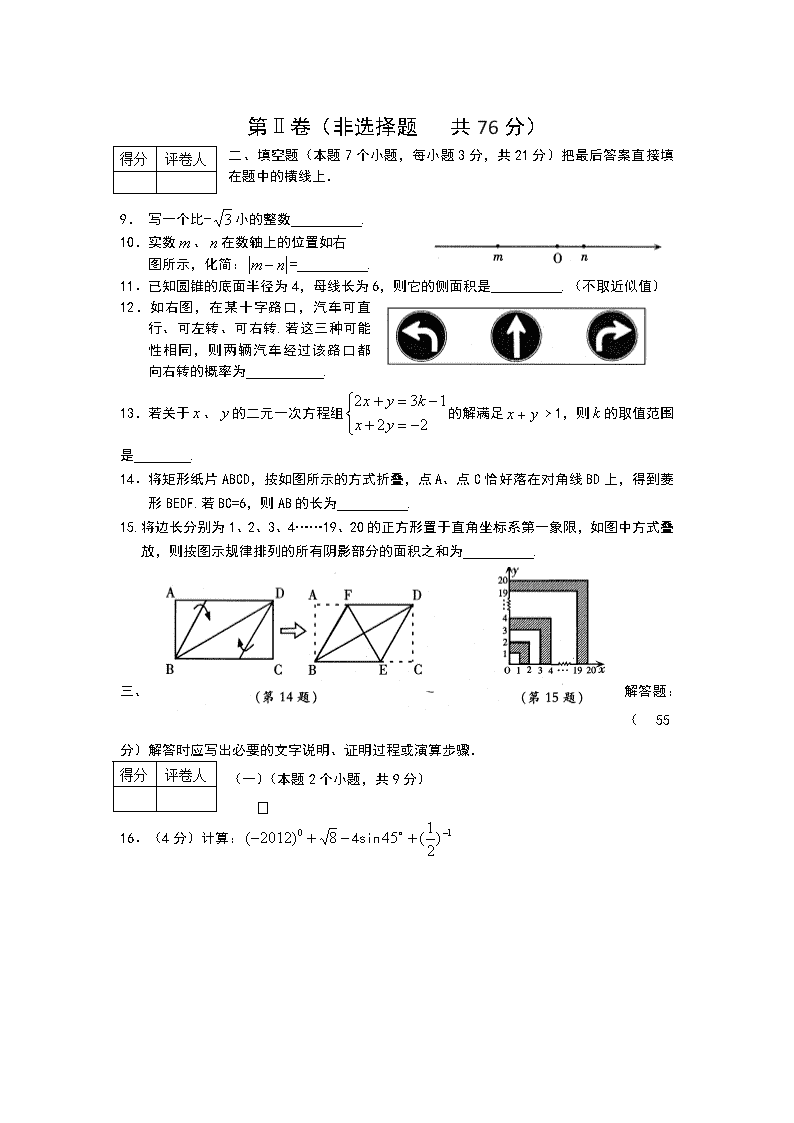
达州市2012年高中阶段教育学校招生统一考试数学本试卷分为第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷1至2页，第Ⅱ卷3至10页．考试时间100分钟，满分100分.第Ⅰ卷（选择题共24分）1.答第Ⅰ卷前，考生务必将姓名、准考证号、考试科目按要求填涂在答题卡上.2.每小题选出答案后，用2B铅笔把答题卡上对应题号的答案标号涂黑，不能将答案答在试题卷上.3.考试结束，将本试卷和答题卡一并交回.一、选择题：（本题8个小题，每小题3分，共24分）在每小题给出的四个选项中，只有一项是符合题目要求的．1．-2的倒数是A、2B、-2C、D、2．下列几何图形中，对称性与其它图形不同的是3．如图，⊙O是△ABC的外接圆，连结OB、OC，若OB=BC，则∠BAC等于A、60°B、45°C、30°D、20°4．今年我市参加中考的学生人数约为人.对于这个近似数，下列说法正确的是A、精确到百分位，有3个有效数字B、精确到百位，有3个有效数字C、精确到十位，有4个有效数字D、精确到个位，有5个有效数字5．2011年达州市各县(市、区)的户籍人口统计表如下：县(市、区)通川区达县开江县宣汉县大竹县渠县万源市人口数（万人）421356013011214559则达州市各县(市、区)人口数的极差和中位数分别是nA、145万人130万人B、103万人130万人C、42万人112万人D、103万人112万人6．一次函数与反比例函数，在同一直角坐标系中的图象如图所示，若﹥，则x的取值范围是A、-2﹤﹤0或﹥1B、﹤-2或0﹤﹤1C、﹥1D、-2﹤﹤17．为保证达万高速公路在2012年底全线顺利通车，某路段规定在若干天内完成修建任务.已知甲队单独完成这项工程比规定时间多用10天，乙队单独完成这项工程比规定时间多用40天,如果甲、乙两队合作，可比规定时间提前14天完成任务.若设规定的时间为x天，由题意列出的方程是A、B、C、D、8．如图，在梯形ABCD中，AD∥BC，E、F分别是AB、CD的中点，则下列结论：①EF∥AD；②S△ABO=S△DCO；③△OGH是等腰三角形；④BG=DG；⑤EG=HF.其中正确的个数是A、1个B、2个C、3个D、4个达州市2012年高中阶段教育学校招生统一考试数学注意事项：1．用蓝黑色钢笔或蓝黑色圆珠笔直接答在试题卷上.2．答卷前将密封线内各项目填写清楚.题号一[来源:学科网]二[来源:Z_xx_k.Com]总分[来源:Z*xx*k.Com]总分人[来源:学|科|网Z|X|X|K]（一）（二）（三）（四）得分n得分评卷人第Ⅱ卷（非选择题共76分）二、填空题（本题7个小题，每小题3分，共21分）把最后答案直接填在题中的横线上．9．写一个比-小的整数.10．实数、在数轴上的位置如右图所示，化简：=.11．已知圆锥的底面半径为4，母线长为6，则它的侧面积是.（不取近似值）12．如右图，在某十字路口，汽车可直行、可左转、可右转.若这三种可能性相同，则两辆汽车经过该路口都向右转的概率为.13．若关于、的二元一次方程组的解满足﹥1，则的取值范围是.14．将矩形纸片ABCD，按如图所示的方式折叠，点A、点C恰好落在对角线BD上，得到菱形BEDF.若BC=6，则AB的长为.15.将边长分别为1、2、3、4……19、20的正方形置于直角坐标系第一象限，如图中方式叠放，则按图示规律排列的所有阴影部分的面积之和为.三、解答题：（55分）解答时应写出必要的文字说明、证明过程或演算步骤．得分评卷人（一）（本题2个小题，共9分）16．（4分）计算：4sinn17．（5分）先化简，再求值：，其中得分评卷人（二）（本题2个小题，共12分）18.（6分）今年5月31日是世界卫生组织发起的第25个“世界无烟日”.为了更好地宣传吸烟的危害，某中学八年级一班数学兴趣小组设计了如下调查问卷，在达城中心广场随机调查了部分吸烟人群，并将调查结果绘制成统计图.n根据以上信息，解答下列问题：（1）本次接受调查的总人数是人，并把条形统计图补充完整.（2）在扇形统计图中，C选项的人数百分比是，E选项所在扇形的圆心角的度数是.（3）若通川区约有烟民14万人，试估计对吸烟有害持“无所谓”态度的约有多少人？你对这部分人群有何建议？19．（6分）大学生王强积极响应“自主创业”的号召，准备投资销售一种进价为每件40元的小家电.通过试营销发现，当销售单价在40元至90元之间（含40元和90元）时，每月的销售量（件）与销售单价（元）之间的关系可近似地看作一次函数，其图象如图所示.（1）求与的函数关系式.（2）设王强每月获得的利润为（元）,求与之间的函数关系式；如果王强想要每月获得2400元的利润，那么销售单价应定为多少元？n得分评卷人（三）（本题2个小题，共15分）20．（7分）数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线.根据以上情境，解决下列问题：①李老师用尺规作角平分线时，用到的三角形全等的判定方法是_________.②小聪的作法正确吗？请说明理由.n③请你帮小颖设计用刻度尺作角平分线的方法.（要求：作出图形，写出作图步骤，不予证明）21．（8分）问题背景若矩形的周长为1，则可求出该矩形面积的最大值.我们可以设矩形的一边长为，面积为，则与的函数关系式为：﹥0），利用函数的图象或通过配方均可求得该函数的最大值.提出新问题若矩形的面积为1，则该矩形的周长有无最大值或最小值？若有，最大（小）值是多少？分析问题若设该矩形的一边长为，周长为，则与的函数关系式为：（﹥0），问题就转化为研究该函数的最大（小）值了.解决问题借鉴我们已有的研究函数的经验，探索函数（﹥0）的最大（小）值.（1）实践操作：填写下表，并用描点法画出函数（﹥0）的图象：（2）观察猜想：观察该函数的图象，猜想当=时，函数（﹥0）有最值（填“大”或“小”），是.（3）推理论证：问题背景中提到，通过配方可求二次函数﹥0）的最大值，请你尝试通过配方求函数（﹥0）的最大（小）值，以证明你的猜想.〔提示：当＞0时，〕n得分评卷人（四）（本题2个小题，共19分）22．(7分)如图，C是以AB为直径的⊙O上一点，过O作OE⊥AC于点E，过点A作⊙O的切线交OE的延长线于点F，连结CF并延长交BA的延长线于点P.（1）求证：PC是⊙O的切线.（2）若AF=1，OA=，求PC的长.23．（12分）如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE.（1）填空：点D的坐标为（），点E的坐标为（）.（2）若抛物线经过A、D、E三点，求该抛物线的解析式.（3）若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在轴上时，正方形和抛物线均停止运动.①在运动过程中，设正方形落在y轴右侧部分的面积为，求关于平移时间（秒）的函数关系式，并写出相应自变量的取值范围.②运动停止时，求抛物线的顶点坐标.n达州市2012年高中阶段教育学校招生统一考试数学参考答案及评分意见一、选择题（本题8个小题.每小题3分，共24分）在每小题给出的四个选项中，只有一项是符合题目要求的.1.D2.A3.C4.B5.D6.A7.B8.D二、填空题：（本题7个小题.每小题3分，共21分）把最后答案直接填在题中的横线上.9.-2（答案不唯一）10.n-m11.24π12.13.k＞214.15.210三、解答题：（55分）解答时应写出必要的文字说明、证明过程或演算步骤16.解：原式=………………………………………………..（2分）=………………………………………………………………….（3分）=3………………………………………………………………………………………..（4分）17.解：原式=……………………………………………………（1分）=……………………………………………………………（2分）=2（+4）=2+8…………………………………………………………………………………….(3分)当a=-1时，原式=2×(-1)+8…………………………………………………………….（4分）n=6……………………………………………………………………….（5分）18.（1）300（1分）补全统计图如下：…………………………………………………………..（2分）（2）26%……………………………………………….（3分）36°………………………………………………….（4分）（3）解：A选项的百分比为：×100%=4%对吸烟有害持“无所谓”态度的人数为：14×4%=0.56（万）………（5分）建议：只要答案合理均可得分………………………………………………..（6分）19.解（1）设与的函数关系式为：由题意得…………………………………………………………………………..（1分）解得………………………………………………………………………….（2分）.∴（40≤≤90）……………………………………………………（3分）（2）由题意得，与的函数关系式为：=………………………………………………………………..（4分）当P=2400时…………………………………………………………（5分）解得,∴销售单价应定为60元或70元……………………………………………………..（6分）20.(1)SSS………………………………………………………………………………（1分）(2)解：小聪的作法正确.理由：∵PM⊥OM,PN⊥ON∴∠OMP=∠ONP=90°在Rt△OMP和Rt△ONP中∵OP=OP,OM=ON∴Rt△OMP≌Rt△ONP（HL）……………………………………………………….（3分）∴∠MOP=∠NOPn∴OP平分∠AOB………………………………………………………………………（4分）（3）解：如图所示.…………………………………………………………………..（6分）步骤：①利用刻度尺在OA、OB上分别截取OG=OH.②连结GH，利用刻度尺作出GH的中点Q.③作射线OQ.则OQ为∠AOB的平分线.………………………………………（7分）20.(1)…………………………………………..（1分）………………………………………….（3分）（2）1、小、4………………………………………………………………………..（5分）（3）证明：………………………………………………（7分）当时，的最小值是4即=1时，的最小值是4………………………………………………………..（8分）n22.（1）证明：连结OC∵OE⊥AC∴AE=CE∴FA=FC∴∠FAC=∠FCA∵OA=OC∴∠OAC=∠OCA∴∠OAC+∠FAC=∠OCA+∠FCA即∠FAO=∠FCO………………………………………………………………….（2分）∵FA与⊙O相切，且AB是⊙O的直径∴FA⊥AB∴∠FCO=∠FAO=90°∴PC是⊙O的切线………………………………………………………………..（3分）（2）∵PC是⊙O的切线∴∠PCO=90°而∠FPA=∠OPC∠PAF=90°∴△PAF∽△PCO…………………………………………………………………..（4分）∴∵CO=OA=,AF=1∴PC=PA…………………………………………………………………..（5分）设PA=，则PC=在Rt△PCO中，由勾股定理得…………………………………………..（6分）解得：∴PC……………………………………………………………………….（7分）23.（1）D（-1，3）、E（-3，2）（2分）（2）抛物线经过（0，2）、（-1，3）、（-3，2），则……………………………………………………………….（3分）n解得∴……………………………………………………….（4分）（3）①当点D运动到y轴上时，t=12.当0＜t≤时，如右图设D′C′交y轴于点F∵tan∠BCO==2,又∵∠BCO=∠FCC′∴tan∠FCC′=2,即=2∵CC′=5t,∴FC′=25t.∴S△CC′F=CC′·FC′=t×t=5t2…………………………………（5分）当点B运动到点C时，t=1.当＜t≤1时，如右图设D′E′交y轴于点G，过G作GH⊥B′C′于H.在Rt△BOC中，BC=∴GH=,∴CH=GH=∵CC′=t,∴HC′=t-,∴GD′=t-∴S梯形CC′D′G=(t-+t)=5t-……………………………（7分）当点E运动到y轴上时，t=.当1＜t≤时，如右图所示设D′E′、E′B′分别交y轴于点M、N∵CC′=t，B′C′=,∴CB′=t-,∴B′N=2CB′=t-∵B′E′=,∴E′N=B′E′-B′N=-tn∴E′M=E′N=(-t)∴S△MNE′=(-t)·(-t)=5t2-15t+∴S五边形B′C′D′MN=S正方形B′C′D′E′-S△MNE′=(5t2-15t+)=-5t2+15t-综上所述，S与x的函数关系式为：当0＜t≤时,S=5当＜t≤1时，S=5t当1＜t≤时，S=-5t2+15t………………………………………………..（9分）②当点E运动到点E′时，运动停止.如下图所示∵∠CB′E′=∠BOC=90°，∠BCO=∠B′CE′∴△BOC∽△E′B′C∴∵OB=2，B′E′=BC=∴∴CE′=∴OE′=OC+CE′=1+=∴E′（0，）…………………………………………………………………..（10分）由点E（-3，2）运动到点E′（0，）,可知整条抛物线向右平移了3个单位，向上平移了个单位.∵=∴原抛物线顶点坐标为（，）……………………………………………（11分）∴运动停止时，抛物线的顶点坐标为（，）…………………………（12分）n