高三交流卷(三)数学(理)试题 Word版含答案

高三交流卷(三)数学(理)试题 Word版含答案

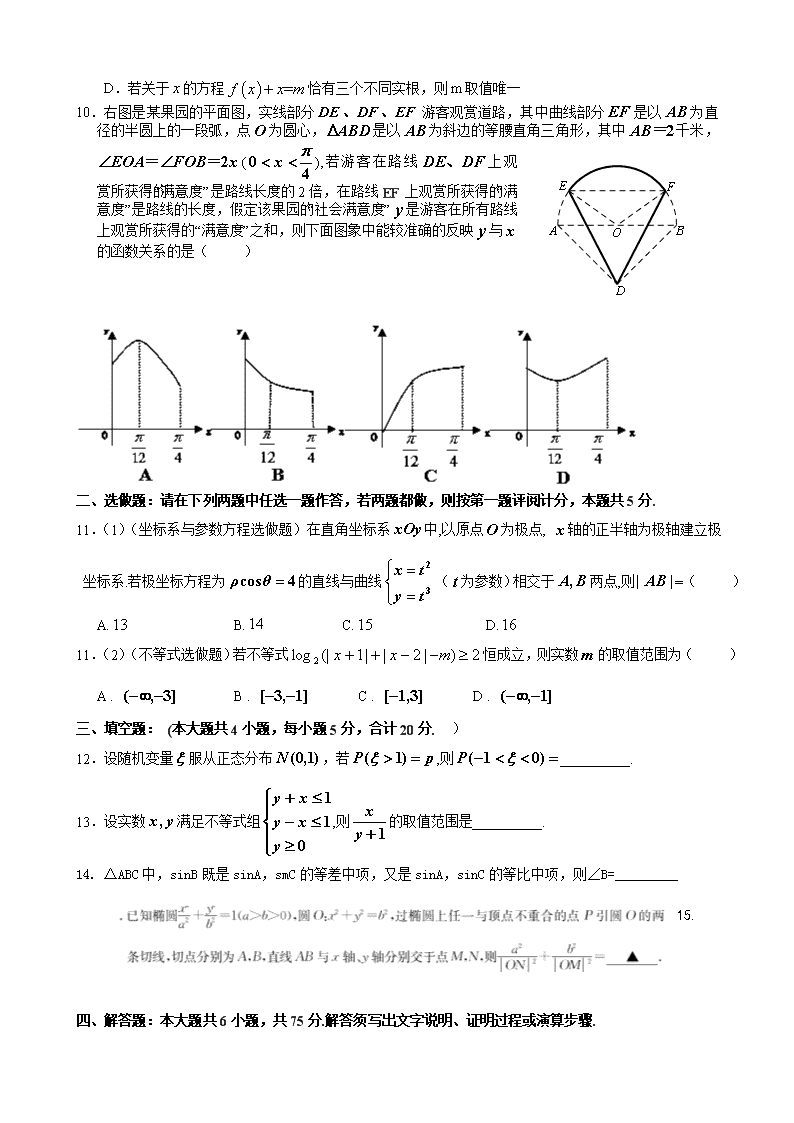
南昌市教研室命制2014届高三交流卷（三）数学（理）试题一、选择题：本大题共10小题，每小题5分，共50分.在每小题所给的四个选项中，只有一项符合题目要求的.1．若集合，集合，则集合的元素的个数为（）A.1B.2C.3D.42．设为虚数单位，则=（）A.B.C.D.3．一个几何体的正视图和侧视图都是边长为1的正方形，则这个几何体的俯视图一定不是（）[学4．已知数列是等比数列，且，则的值为（）A.B.C.D.5．从编号为001,002,……,500的500个产品中用系统抽样的方法抽取一个样本，已知样本中编号最小的两个编号分别为007,032，则样本中最大的编号应该为（）A.480B.481C.482D.4836．如图，矩形ABCD中，E为边AD上的动点，将△ABE沿直线BE翻转成△A1BE，使平面A1BE平面ABCD，则点A1的轨迹是（）A．线段B．圆弧C．椭圆的一部分D．以上答案都不是7．AD,BE分别是DABC的中线，若||=||=1，且与的夹角为120°，则·=（）A．B．C．D．8．已知双曲线的左右焦点分别为，为双曲线的离心率，是双曲线右支上的点，的内切圆的圆心为，过作直线的垂线，垂足为，则线段的长度为（）A．B.C．D．9．函数，直线与函数的图像相交于四个不同的点，从小到大，交点横坐标依次记为，下列说法错误的是（）A．B．C．nD．若关于的方程恰有三个不同实根，则取值唯一10．右图是某果园的平面图，实线部分游客观赏道路，其中曲线部分是以为直径的半圆上的一段弧，点为圆心，是以为斜边的等腰直角三角形，其中千米，(),若游客在路线上观赏所获得的“满意度”是路线长度的2倍，在路线EF上观赏所获得的“满意度”是路线的长度，假定该果园的“社会满意度”是游客在所有路线上观赏所获得的“满意度”之和，则下面图象中能较准确的反映与的函数关系的是（）二、选做题：请在下列两题中任选一题作答，若两题都做，则按第一题评阅计分，本题共5分.11．（1）（坐标系与参数方程选做题）在直角坐标系中,以原点为极点,轴的正半轴为极轴建立极坐标系.若极坐标方程为的直线与曲线（为参数）相交于两点,则=（）A.B.C.D.11．（2）（不等式选做题）若不等式恒成立，则实数的取值范围为（）A.B.C.D.三、填空题：(本大题共4小题，每小题5分，合计20分.[来源]J）12．设随机变量服从正态分布，若,则__________.13．设实数满足不等式组,则的取值范围是__________.14.△ABC中，sinB既是sinA，smC的等差中项，又是sinA，sinC的等比中项，则∠B=_________15.四、解答题：本大题共6小题，共75分.解答须写出文字说明、证明过程或演算步骤.n16．（本小题满分12分）设a∈R，函数f（x）＝cos（asinx－cosx）＋满足（1）求f（x）的单调递减区间；（2）设锐角△ABC的内角A、B、C所对的边分别为a、b、c，且，求f（A）的取值范围．17．（本小题满分12分）已知A箱装有编号为的五个小球（小球除编号不同之外，其他完全相同），B箱装有编号为的两个小球（小球除编号不同之外，其他完全相同）,甲从A箱中任取一个小球，乙从B箱中任取一个小球，用分别表示甲，乙两人取得的小球上的数字.（1）求概率；（2）设随机变量，求的分布列及数学期望.18．（本小题满分12分）已知数列中，，当时，.(1)求数列的通项公式.(2)设,数列前项的和为,求证:.n19．（本小题满分12分）如图1，直角梯形中，，分别为边和上的点，且，．将四边形沿折起成如图2的位置，使．（1）求证：平面；（2）求平面与平面所成锐角的余弦值.21．（本题满分14分）已知（）（Ⅰ）若方程有3个不同的根，求实数的取值范围；（Ⅱ）在（Ⅰ）的条件下，是否存在实数，使得在上恰有两个极值点，且满足，若存在，求实数的值，若不存在，说明理由．n答案一、选择题：题号1234567891011答案ACBACDCBDAD三、填空题：11．12．13．14．四、解答题：n（2）如图以中点为原点，为轴建立如图所示的空间直角坐标系，则，，，所以的中点坐标为因为，所以易知是平面的一个法向量，设平面的一个法向量为由令则，，20.解：（1）设点，由题知|AB|-|AC|=|BE|-|CE|=|CE|+2|OE|-|CE|=2n根据双曲线定义知，点A的轨迹是以B、C为焦点，实轴长为2的双曲线的右支除去点E（1，0），故R的方程为……………………4分（2）设点由（I）可知……………………6分①当直线轴时点在轴上任何一点处都能使得成立②当直线MN不与轴垂直时，设直线由得……………………9分要使，只需成立……………………10分即即即故,故所求的点Q的坐标为时使成立.……………………13分21．（Ⅰ）解：由得：或可得或且n∵方程有3个不同的根，∴方程有两个不同的根∴又∵，且要保证能取到0∴即∴．（Ⅱ）解：∵令，设∴∵∴∴∵∴，∴∴存在，使得，另外有，使得假设存在实数，使得在上恰有两个极值点，且满足则存在，使得，另外有，即∴，∴，即即（*）设∴∵∴∴∴在上是增函数∴∴方程（*）无解，即不存在实数，使得在上恰有两个极值点，且满足