2010级工管运筹学试卷B参考答案

2010级工管运筹学试卷B参考答案

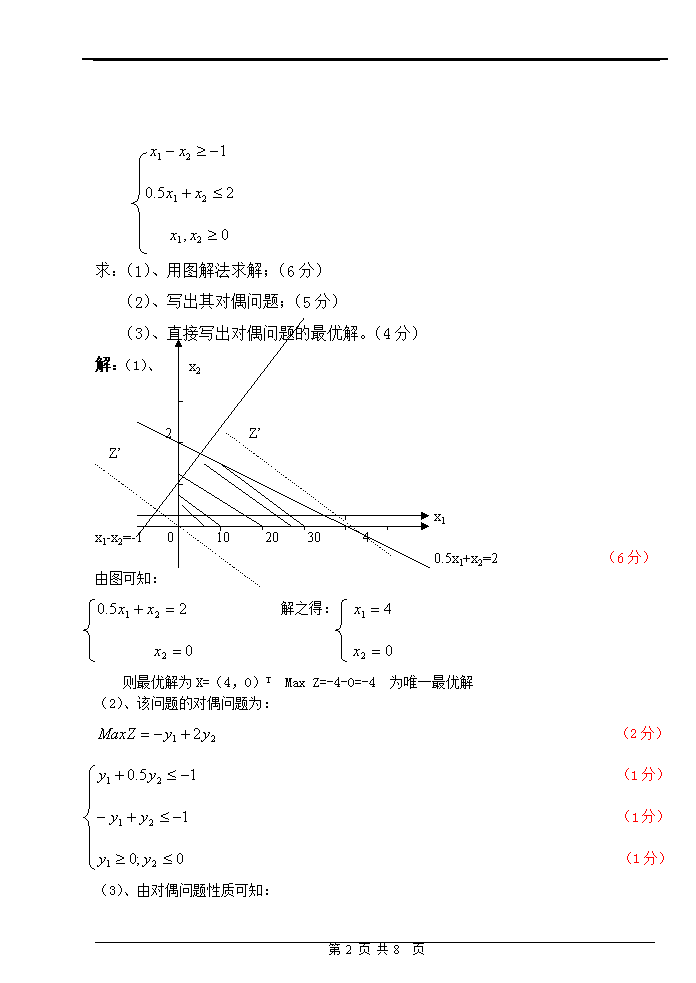
承诺：我将严格遵守考场纪律，知道考试违纪、作弊的严重性，还知道请他人代考或代他人考者将被开除学籍和因作弊受到记过及以上处分将不授予学士学位，愿承担由此引起的一切后果。专业班级学号学生签名：华东交通大学2011—2012学年第二学期考试卷　　　　　　　　　　　　　　　　　　　　试卷编号：　　　　（　B）卷运筹学课程课程类别：必闭卷（）　　　　　考试日期：　　　　题号一二三四五六七八九十总分累分人签名题分1023301522100得分考生注意事项：1、本试卷共8页，总分　100　分，考试时间　120　　分钟。2、考试结束后，考生不得将试卷、答题纸和草稿纸带出考场。得分评阅人一、填空题(每空2分，共10分)1、运输问题中求初始基本可行解的方法通常有：最小元素法、伏格尔法及西北角法三种方法。2、若原问题为无界解，则对偶问题的解是无可行解。3、影子价格是指：在其它条件不变的情况下，单位资源变化对目标函数的最优值的变化。4、在线性规划问题中，图解法适合用于处理变量为两个的线性规划问题。二、综合题（共15分）得分评阅人用图解法求解下列目标规划（15分）第8页共8页n求：（1）、用图解法求解；（6分）（2）、写出其对偶问题；（5分）（3）、直接写出对偶问题的最优解。（4分）解：（1）、x22Z’Z’x1x1-x2=-1010203040.5x1+x2=2（6分）由图可知：解之得：则最优解为X=（4，0）TMaxZ=-4-0=-4为唯一最优解（2）、该问题的对偶问题为：（2分）（1分）（1分）（1分）（3）、由对偶问题性质可知：第8页共8页n解之得：所以Y*=（0，-2）TMaxZ=-4（4分）2、有一整数规划模型为：MaxZ=x1+x22x1+x2≤64x1+5x2≤20x1、x2≥0且为整数已知经过中间计算，其单纯形表如下：Cj11000CbXbbX1X2X3X4X5100X1X2X49/512/54/51010-1/501-102/50011-6/5σj0000-1/5试写出其合适的Gomory割平面方程（8分）。解：选x1或x4对应的约束方程为调整对象。X1对应的Gomory割平面方程：X4对应的Gomory割平面方程：三、计算题(共30分)得分评阅人1、已知下列线性规划问题：（20分）第8页共8页n求：用单纯形法求解，并指出问题属于哪一类解。解：（1）、将原问题划为标准形得：=60（4分）（计算表每步4分）6-33000b060311100020[2]-2401006033-30016-330006-33000b03004-51-3/206101-1201/200300[6]-90-3/2103-90-306-33000b0100011-1/2-2/3615101/201/41/6-3501-3/20-1/41/600-9/20-9/4-1/2所以X=（15，5，0，10，0，0）T为唯一最优解（2分）MaxZ=6*15-3*5=75（2分）2、某公司下属的3个分厂A1、A2、A3生产质量相同的工艺品，要运输到B1、B2、B3、B4，4个销售点，分厂产量、销售点销量、单位物品的运费数据如下：第8页共8页nB1B2B3B4产量aiA12311201537A21816171434A32215121329销量bj23162519试用最小元素法求出初始运输方案，并求出该方案的运输费用总和。（10分）（要求另外列表表示运输方案，并列出简要的计算过程）解：该问题为产销不平衡问题，∑产量=37+34+29=100；∑销量=23+16+25+19=83；产量大于销量。增加虚拟的销地B5，（2分）得产销平衡表如下：（3分）B1B2B3B4B5产量aiA123112015037A218161714034A322151213029销量bj2316251917100按最小元素法求出的初始方案为：（4分）B1B2B3B4B5产量aiA14⑦16②17①37A219⑥15⑤34A325③4④29销量bj2316251917100总运输费用=4*23+19*18+16*11+25*12+15*14+4*13+17*0=1172（1分）四、证明题(共15分)得分评阅人1、某工厂按合同每年需提供D个产品，不许缺货。假设每一周期工厂需装配费C3元，存储费每年每单位为C1元。证明：全年每次最佳的订购数量为Qmin时，最经济。其中：。第8页共8页n2、五、建模题(共22分)第8页共8页n得分评阅人1、某企业生产3种产品甲、乙、丙，产品所需的主要原料有A、B两种，原料A每单位分别可生产产品甲、乙、丙底座12、18、16个；产品甲、乙、丙每个需要原料B分别为13kg、8kg、10kg，设备生产用时分别为10.5、12.5、8台时，每个产品的利润分别为1450元、1650元、1300元。按月计划，可提供的原料A为20单位，原料B350kg，设备月正常的工作时间为3000台时。建立实现总利润最高的数学模型(不需要计算结果)。（10分）解：决策变量：设种产品甲、乙、丙的产量分别为：x1,x2,x3。1分目标函数：2分约束方程：2、某工厂某种型号设备可在高、低两种不同的负荷下进行生产，该设备在高负荷下生产的产量函数为，其中，u为投入高负荷设备的数量，年设备完好率a=0.65；该设备在低负荷下生产的产量函数为，其中，y为投入低负荷设备的数量；年设备完好率b=0.85。假设开始生产时完好设备的数量为S=1000台，试问每年如何安排生产，使得设备在4年内生产的产品数量最大？建立该问题的动态规划数学模型。(具体内容包括：阶段、状态变量、决策变量、决策变量允许取值范围、状态转移方程、阶段指标、递推方程、边界条件的定义，不要求计算求解)。（12分）第8页共8页n第8页共8页