- 2022-04-09 发布 |
- 37.5 KB |
- 5页
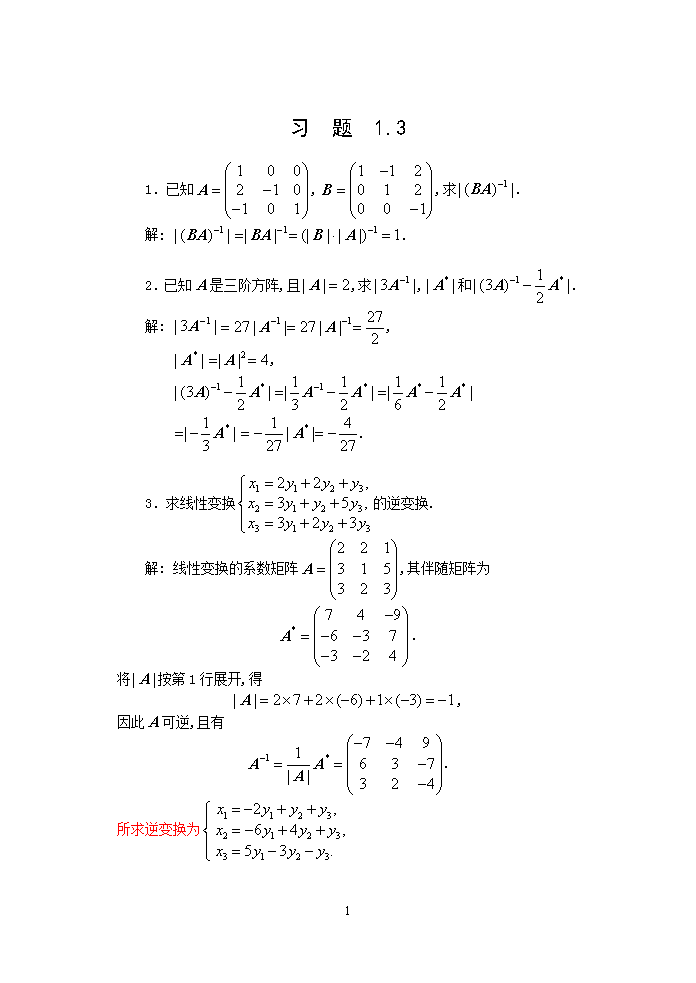

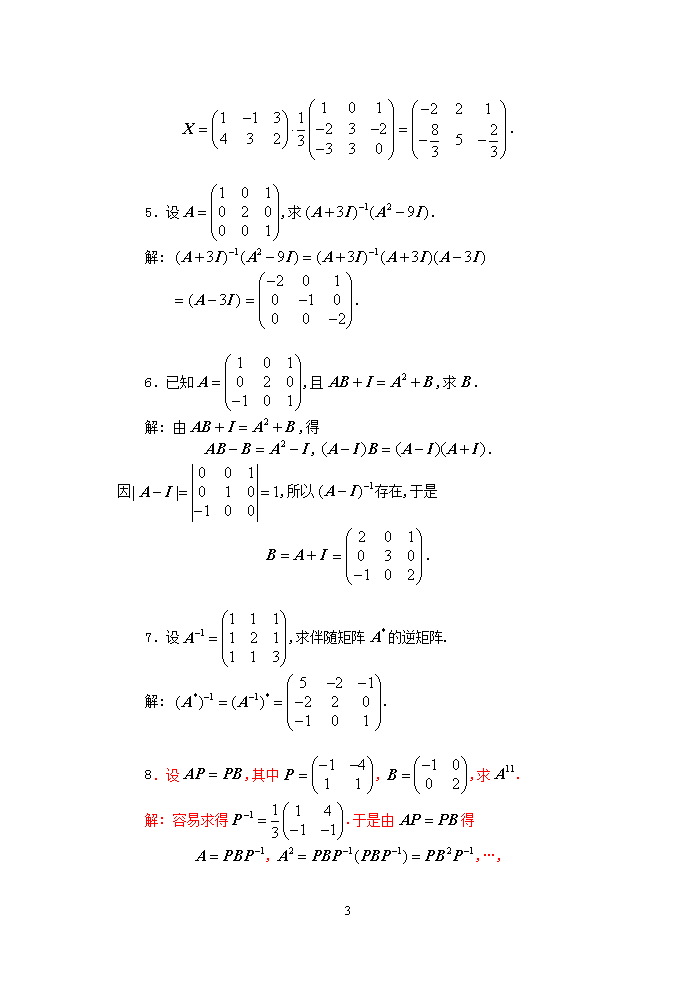
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
简明线性代数 课后答案 1-3
习题1.31.已知,,求.解:.2.已知是三阶方阵,且,求,和.解:,,.3.求线性变换的逆变换.解:线性变换的系数矩阵,其伴随矩阵为.将按第1行展开,得,因此可逆,且有.所求逆变换为5n4.利用逆矩阵求以下方程的解:(1);解:记矩阵,其伴随矩阵.将按第1行展开,得,因此可逆,且有.所求解为.(2).解:记矩阵,其伴随矩阵.将按第1行展开,得,因此可逆,且有.所求解为5n.5.设,求.解:.6.已知,且,求.解:由,得,.因,所以存在,于是.7.设,求伴随矩阵的逆矩阵.解:.8.设,其中,,求.解:容易求得.于是由得,,…,5n.9.设,且,求.解:由,得.,,,因此可逆,且有.由,得.10.设,证明.证明:由,得,因此.11.设方阵满足方程,证明可逆,并求其逆矩阵.证明:由,得,因此可逆,且有.5n12.设为可逆矩阵,与同阶,且满足,证明和均为可逆矩阵.证明:因为可逆矩阵,所以.由,得,两边取行列式,得,(为与的阶数).于是,,所以和均为可逆矩阵.5查看更多