2011届中考数学一轮专题复习测试题9(锐角三角函数有答案)[1]

2011届中考数学一轮专题复习测试题9(锐角三角函数有答案)[1]

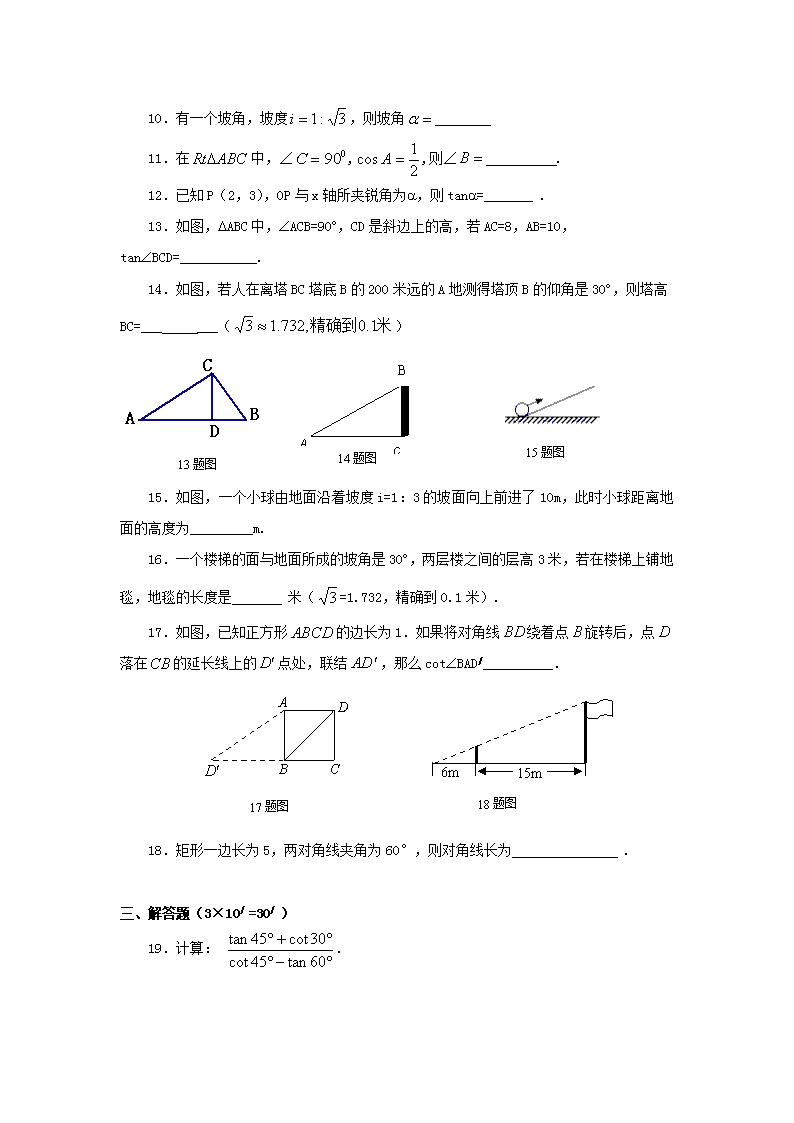
图形与几何（锐角三角函数）一、教材内容九年级第一学期：第二十五章锐角的三角比（11课时）[来源:学科网]二、“课标”要求1．理解锐角三角比的概念，会求特殊锐角的三角比值。2．理解解直角三角形的意义，会用锐角互余、锐角三角比和勾股定理等解直角三角形和解决一些简单的实际问题。[来源:学科网]说明：锐角三角比只涉及正弦、余弦、正切、余切，注重建立直角三角形的边角关系，对三角比之间的关系不作要求。三、“考纲”要求考点要求40、锐角三角比（锐角的正弦、余弦、正切、余切）的概念，30度、45度、60度角的三角比值II41、解直角三角形及其应用III[来源:学科网]n图形与几何（7）（锐角的三角比）一、选择题（6×4/=24/）1．在中，∠，，，则的值是（）（A）；（B）；（C）；（D）2.2．如果中各边的长度都扩大到原来的2倍，那么锐角∠的三角比的值（）（A）都扩大到原来的2倍；（B）都缩小到原来的一半；（C）没有变化；（D）不能确定.3．等腰三角形的底边长10cm，周长36cm，则底角的余弦值为……（）(A)；(B)；(C)；(D).4．在中，∠，，则的值为……（）（A）；（B）；（C）；（D）.5．在Rt△ABC中，∠C=90°，∠A的对边为a，已知∠A和边a，求边c，则下列关系中正确的是…………………………………………………………………()（A）；（B）；（C）a=b×tanA；（D）．6．在△ABC中，若，，则这个三角形一定是……（   ）  （A）锐角三角形;       （B）直角三角形; （C）钝角三角形;    （C）等腰三角形.二、填空题（12×4/=48/）7．在RtΔABC中，∠,若AB=5,BC=3,，则=，，，[来源:Z|xx|k.Com]8．在中，∠，∠=30°，AC=3,则BC=.9.在△ABC中，∠C=90°，，则sinB的值是________.n10．有一个坡角，坡度，则坡角11．在中，∠,,则∠.12．已知P（2，3），OP与x轴所夹锐角为a，则tana=_______.13．如图，DABC中，ÐACB=90°，CD是斜边上的高，若AC=8，AB=10，tanÐBCD=___________.14．如图，若人在离塔BC塔底B的200米远的A地测得塔顶B的仰角是30°，则塔高BC=______（）_C_A14题图B15题图13题图_15．如图，一个小球由地面沿着坡度i=1：3的坡面向上前进了10m，此时小球距离地面的高度为_________m.　　　　16．一个楼梯的面与地面所成的坡角是30°，两层楼之间的层高3米，若在楼梯上铺地毯，地毯的长度是米（=1.732，精确到0.1米）.[来源:学科网]17．如图，已知正方形的边长为1．如果将对角线绕着点旋转后，点落在的延长线上的点处，联结，那么cotÐBAD/__________．6m15m18题图ADCB17题图18．矩形一边长为5，两对角线夹角为60°，则对角线长为.三、解答题（3×10/=30/）19．计算：.n20．已知直线交x轴于A，交y轴于B，求ÐABO的正弦值．[来源:学。科。网]21．如图，将正方形ABCD的边BC延长到点E，使CE=AC，AE与CD相交于点F.求∠E的余切值.EFBCDA21题图四、解答题（4×12/=48/）22．某人要测河对岸的树高，在河边A处测得树顶仰角是60°，然后沿与河垂直的方向后退10米到Ｂ处，再测仰角是30°，求河对岸的树高。（精确到0.1米）．ABC0.5m3m23题图23．如图所示，秋千链子的长度为3m，静止时的秋千踏板（大小忽略不计）距地面0.5m．秋千向两边摆动时，若最大摆角（摆角指秋千链子与铅垂线的夹角）约为，则秋千踏板与地面的最大距离约为多少？(参考数据：≈0.8,≈0.6)n[来源:Z,xx,k.Com]24．某风景区内有一古塔AB，在塔的北面有一建筑物，当光线与水平面的夹角是30°时，塔在建筑物的墙上留下了高3米的影子CD；而当光线与地面的夹角是45°时，塔尖A在地面上的影子E与墙角C有15米的距离（B、E、C在一条直线上），求塔AB的高度（结果保留根号）．BAEDC45°30°24题图25．如图，ABCD为正方形，E为BC上一点，将正方形折叠，使A点与E点重合，折痕为MN，若.   （1）求△ANE的面积；（2）求sin∠ENB的值.[来源:学科网ZXXK]n参考答案1．A；2．C；3．C；4．C；5．B；6．A．7．；；；8．；　9.　10．30°；11．30°；12．；13．；14．115.5米；　　15．；16．8.2；　　17．；18．10或．19．解：原式＝　　…………………………………………4分＝　　　　　……………………………4分＝－２－　　　　　　　…………………2分20．解：令x=0，得y=4.令y=0，得x=—3．则A（-3，0），B（0，4）……………………………2分∴OA=3，OB=4.∵∠AOB=90°.∴AB=5…………………………2分∴sin∠ABO=……………………………………4分=.………………………2分21．解：设正方形边长为a,则AB=BC=a………………………………………1分∵四边形ABCD是正方形∴∠B=90°　∴AC=a…………………4分∴CE=AC=a…………………………………2分n∴cot∠E==+1………………………3分22．　解：如图，由题意得∠CAD=60°，∠CBD=30°，AB=10米，设AD=x米,………2分在RtΔACD中CD=AD·tan∠CAD=x　　　…………………………………4分在RtΔACD中BD=CD·cot∠CBD=3x　　　…………………………………3分∴AB=2x=10∴x=5∴CD=x=5≈8.7…………………………2分答：河对岸的树高约为8.7米．…………………………１分23．解：过Ｃ作CD⊥AB于Ｄ则∠ADC=90°……………………………1分在Rt△ACD中∵cos∠DAC=…………………………………………4分∴AD=3·cos530≈1.8…………………………………2分∴BD=BA-AD=3-1.8=1.2…………………………………2分[来源:学科网]∴1.2+0.5=1.7(m)…………………………………………2分答：秋千踏板与地面的最大距离约为1.7米……………………………………1分24．解：过点D作DF⊥AB，垂足为点F．…………………………………………1分[来源:Z&xx&k.Com]∵AB⊥BC，CD⊥BC，∴四边形BCDF是矩形，∴BC＝DF，CD＝BF．……2分设AB＝x米，在Rt△ABE中，∠AEB＝∠BAE＝45°，∴BE＝AB＝x．……2分在Rt△ADF中，∠ADF＝30°．AF＝AB－BF＝x－3，AEDC45°FB∴DF＝AF·cot30°＝（x－3）．……4分∵DF＝BC＝BE＋EC，∴（x－3）＝x＋15，∴x＝12＋9……………………………2分．答：塔AB的高度是（12＋9）米．…1分n25．解：∵----------------------1分∴设BE=a，AB=3a，则CE=2a∵DC+CE=10,3a+2a=10，∴a=2.----------------------2分∴BE=2，AB=6，CE=4.∵.----------------------1分又.----------------------1分[来源:Zxxk.Com]∴----------------------2分∴----------------------2分sin----------------------3分