杭州中考数学复习第五章四边形第二节平行四边形同步测试

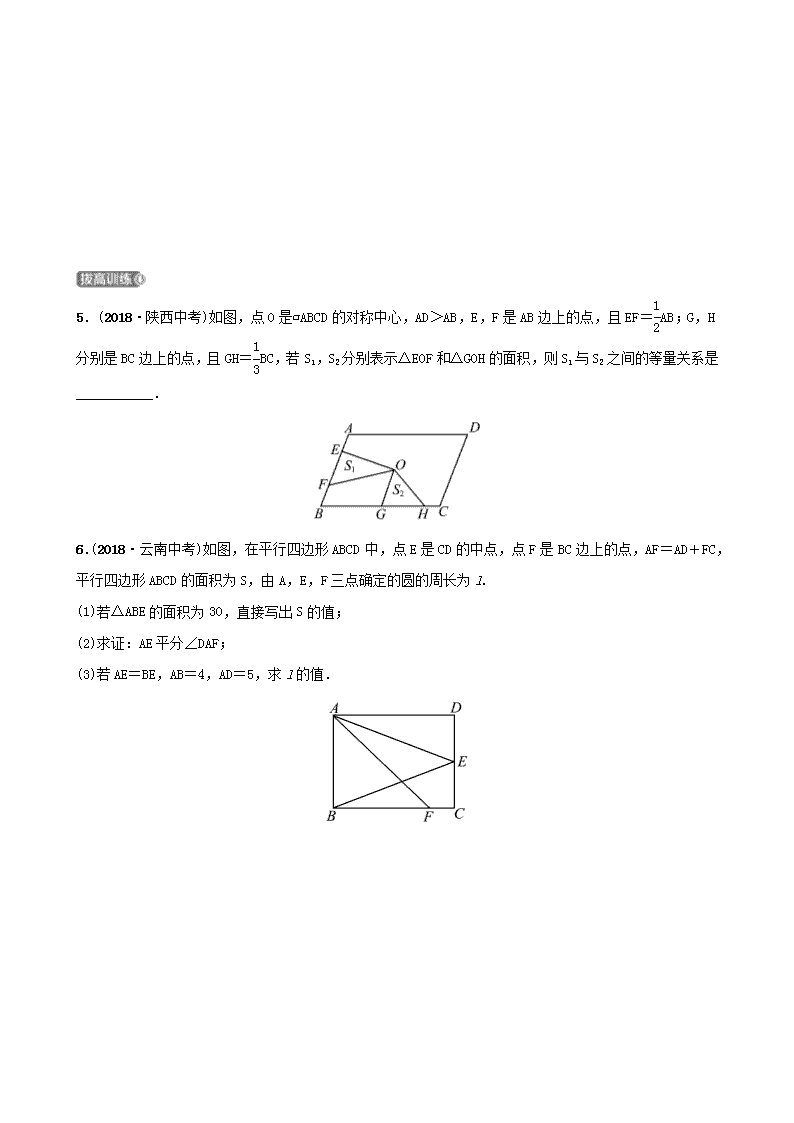
杭州中考数学复习第五章四边形第二节平行四边形同步测试

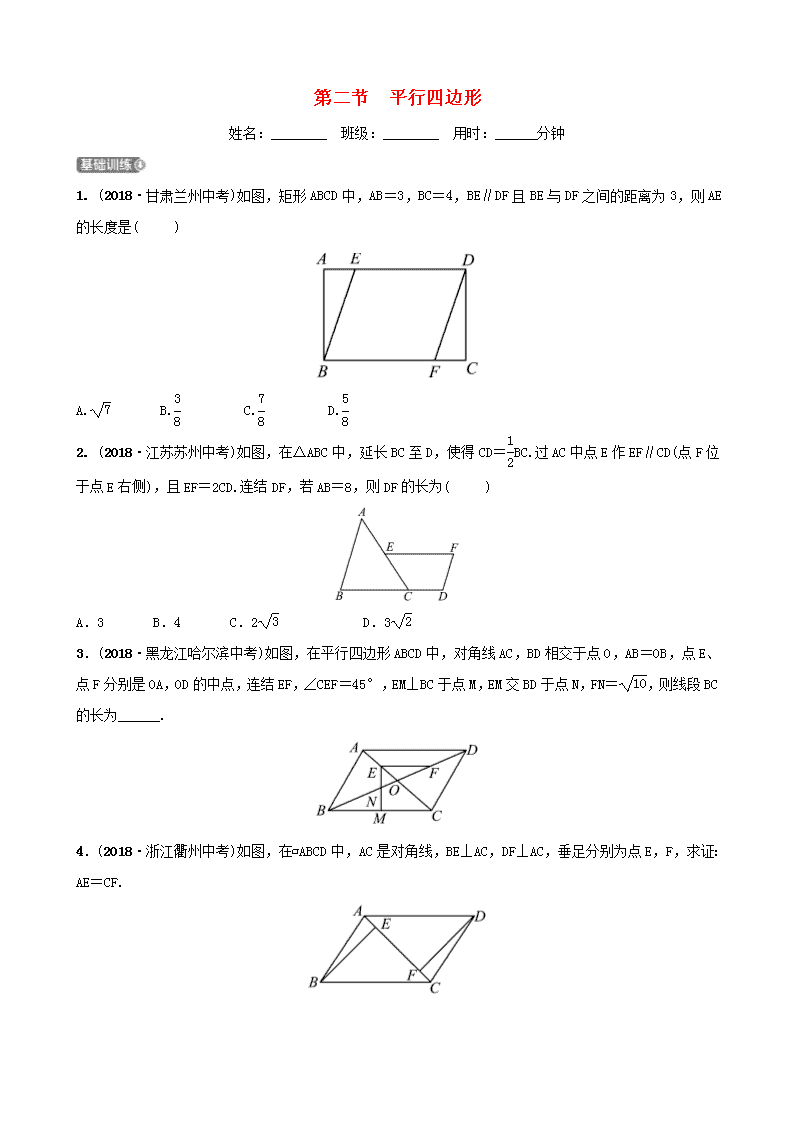
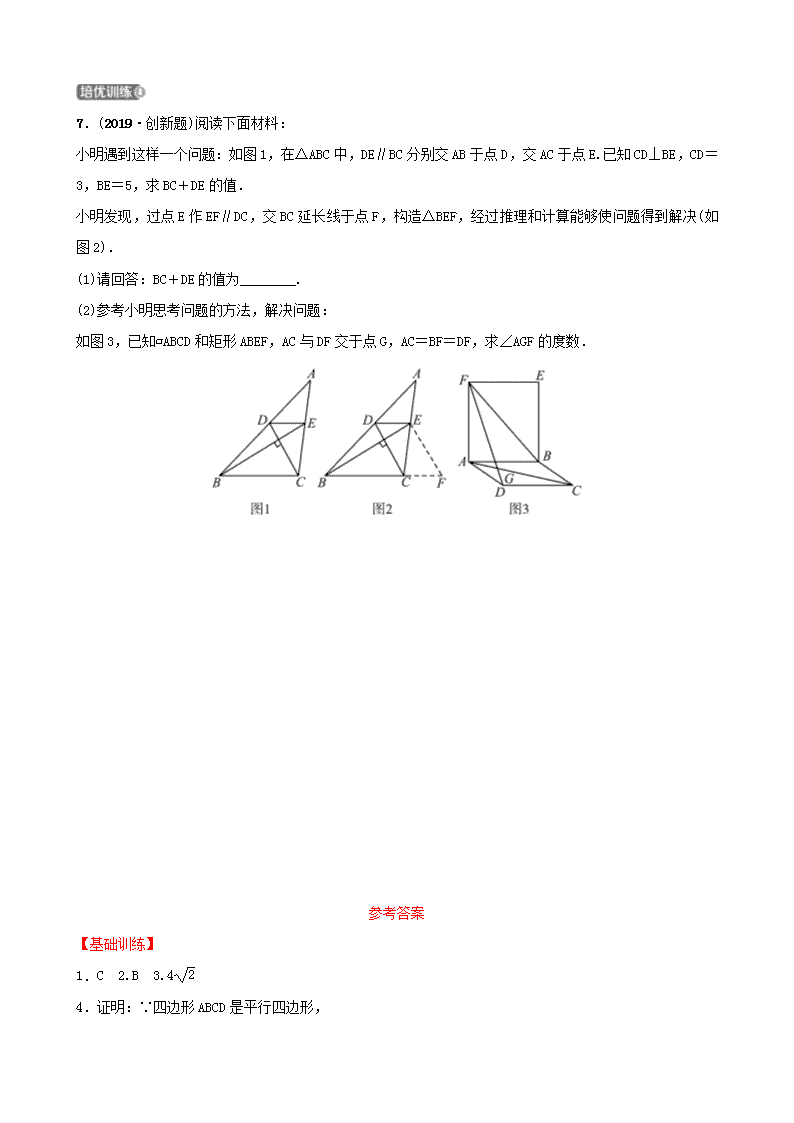
第二节　平行四边形姓名：________　班级：________　用时：______分钟1.(2018·甘肃兰州中考)如图，矩形ABCD中，AB＝3，BC＝4，BE∥DF且BE与DF之间的距离为3，则AE的长度是()A.B.C.D.2.(2018·江苏苏州中考)如图，在△ABC中，延长BC至D，使得CD＝BC.过AC中点E作EF∥CD(点F位于点E右侧)，且EF＝2CD.连结DF，若AB＝8，则DF的长为()A．3B．4C．2D．33．(2018·黑龙江哈尔滨中考)如图，在平行四边形ABCD中，对角线AC，BD相交于点O，AB＝OB，点E、点F分别是OA，OD的中点，连结EF，∠CEF＝45°，EM⊥BC于点M，EM交BD于点N，FN＝，则线段BC的长为______.4．(2018·浙江衢州中考)如图，在▱ABCD中，AC是对角线，BE⊥AC，DF⊥AC，垂足分别为点E，F，求证：AE＝CF.n5．(2018·陕西中考)如图，点O是▱ABCD的对称中心，AD＞AB，E，F是AB边上的点，且EF＝AB；G，H分别是BC边上的点，且GH＝BC，若S1，S2分别表示△EOF和△GOH的面积，则S1与S2之间的等量关系是___________．6．(2018·云南中考)如图，在平行四边形ABCD中，点E是CD的中点，点F是BC边上的点，AF＝AD＋FC，平行四边形ABCD的面积为S，由A，E，F三点确定的圆的周长为l.(1)若△ABE的面积为30，直接写出S的值；(2)求证：AE平分∠DAF；(3)若AE＝BE，AB＝4，AD＝5，求l的值．n7．(2019·创新题)阅读下面材料：小明遇到这样一个问题：如图1，在△ABC中，DE∥BC分别交AB于点D，交AC于点E.已知CD⊥BE，CD＝3，BE＝5，求BC＋DE的值．小明发现，过点E作EF∥DC，交BC延长线于点F，构造△BEF，经过推理和计算能够使问题得到解决(如图2)．(1)请回答：BC＋DE的值为________.(2)参考小明思考问题的方法，解决问题：如图3，已知▱ABCD和矩形ABEF，AC与DF交于点G，AC＝BF＝DF，求∠AGF的度数．参考答案【基础训练】1．C　2.B　3.44．证明：∵四边形ABCD是平行四边形，n∴AB＝CD，AB∥CD，∴∠BAE＝∠DCF.又BE⊥AC，DF⊥AC，∴∠AEB＝∠CFD＝90°.在△ABE与△CDF中，∴△ABE≌△CDF，∴AE＝CF.【拔高训练】5.＝6．(1)解：如图，作EG⊥AB于点G，则S△ABE＝×AB×EG＝30，则AB·EG＝60，∴平行四边形ABCD的面积为60.(2)证明：如图，延长AE交BC延长线于点H.∵四边形ABCD是平行四边形，∴AD∥BC，∴∠ADE＝∠HCE，∠DAE＝∠CHE.∵E为CD的中点，∴CE＝ED，∴△ADE≌△HCE，∴AD＝HC，AE＝HE，∴AD＋FC＝HC＋FC.由AF＝AD＋FC和FH＝HC＋FC得AF＝FH，∴∠FAE＝∠CHE.又∵∠DAE＝∠CHE，∴∠DAE＝∠FAE，∴AE平分∠DAF.n(3)解：如图，连结EF.∵AE＝BE，AE＝HE，∴AE＝BE＝HE，∴∠BAE＝∠ABE，∠HBE＝∠BHE.∵∠DAE＝∠CHE，∴∠BAE＋∠DAE＝∠ABE＋∠HBE，即∠DAB＝∠CBA.由四边形ABCD是平行四边形得∠DAB＋∠CBA＝180°，∴∠CBA＝90°，∴AF2＝AB2＋BF2＝16＋(5－FC)2＝(FC＋CH)2＝(FC＋5)2，解得FC＝，∴AF＝FC＋CH＝.∵AE＝HE，AF＝FH，∴FE⊥AH，∴AF是△AEF的外接圆直径，∴△AEF的外接圆的周长l＝π.【培优训练】7．解：(1)(2)如图，连结AE，CE.∵四边形ABCD是平行四边形，∴AB∥DC.n∵四边形ABEF是矩形，∴AB∥FE，BF＝AE.∴DC∥FE.∴四边形DCEF是平行四边形．∴CE∥DF.∵AC＝BF＝DF，∴AC＝AE＝CE，∴△ACE是等边三角形．∴∠ACE＝60°.∵CE∥DF，∴∠AGF＝∠ACE＝60°.