2018_2019学年高中数学第三章导数及其应用3.3导数在研究函数中的应用3.3.3函数的最大(小)值与导数讲义
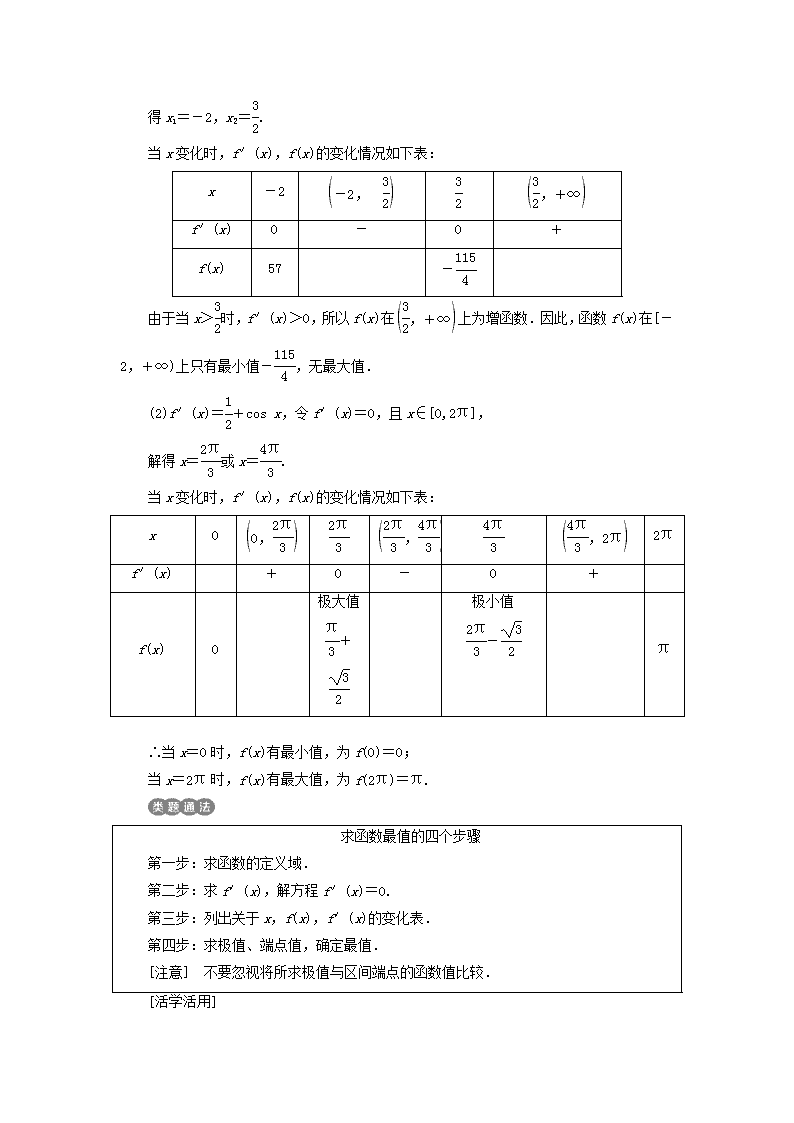
3.3.3 函数的最大(小)值与导数预习课本P96~98,思考并完成以下问题1.什么是函数的最值?函数在闭区间上取得最值的条件是什么? 2.函数的最值与极值有什么关系? 3.求函数最值的方法和步骤是什么? 1.函数y=f(x)在闭区间[a,b]上取得最值的条件如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.[点睛] 对函数最值的三点说明(1)闭区间上的连续函数一定有最值,开区间内的连续函数不一定有最值.若有唯一的极值,则此极值必是函数的最值.(2)函数的最大值和最小值是一个整体性概念.(3)函数y=f(x)在[a,b]上连续,是函数y=f(x)在[a,b]上有最大值或最小值的充分而非必要条件.2.求函数y=f(x)在[a,b]上的最大值与最小值的步骤(1)求函数y=f(x)在(a,_b)内的极值.n(2)将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.[点睛] 函数极值与最值的关系(1)函数的极值是函数在某一点附近的局部概念,函数的最大值和最小值是一个整体性概念.(2)函数的最大值、最小值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,函数的极值可以有多个,但最值只能有一个.(3)极值只能在区间内取得,最值则可以在端点处取得.有极值的未必有最值,有最值的未必有极值;极值有可能成为最值,最值不在端点处取得时必定是极值.1.判断下列命题是否正确.(正确的打“√”,错误的打“×”)(1)函数的最大值一定是函数的极大值( )(2)开区间上的单调连续函数无最值( )(3)函数f(x)在区间[a,b]上的最大值和最小值一定在两个端点处取得( )答案:(1)× (2)√ (3)×2.函数f(x)=x3-3x2+2在区间[-1,1]上的最大值是( )A.-2 B.0C.2D.4答案:C3.函数f(x)=3x+sinx在x∈[0,π]上的最小值为________.答案:14.已知f(x)=-x2+mx+1在区间[-2,-1]上的最大值就是函数f(x)的极大值,则m的取值范围是________.答案:(-4,-2)求函数的最值[典例] 求下列函数的最值.(1)f(x)=4x3+3x2-36x+5,x∈[-2,+∞);(2)f(x)=x+sinx,x∈[0,2π].[解] (1)f′(x)=12x2+6x-36,令f′(x)=0,n得x1=-2,x2=.当x变化时,f′(x),f(x)的变化情况如下表:x-2f′(x)0-0+f(x)57-由于当x>时,f′(x)>0,所以f(x)在上为增函数.因此,函数f(x)在[-2,+∞)上只有最小值-,无最大值.(2)f′(x)=+cosx,令f′(x)=0,且x∈[0,2π],解得x=或x=.当x变化时,f′(x),f(x)的变化情况如下表:x02πf′(x)+0-0+f(x)0极大值+极小值-π∴当x=0时,f(x)有最小值,为f(0)=0;当x=2π时,f(x)有最大值,为f(2π)=π.求函数最值的四个步骤第一步:求函数的定义域.第二步:求f′(x),解方程f′(x)=0.第三步:列出关于x,f(x),f′(x)的变化表.第四步:求极值、端点值,确定最值.[注意] 不要忽视将所求极值与区间端点的函数值比较. [活学活用]n已知函数f(x)=+lnx,求f(x)在上的最大值和最小值.解:易知f(x)的定义域为(0,+∞),f(x)=+lnx=-1+lnx,∴f′(x)=-+=.令f′(x)=0,得x=1.当x变化时,f′(x)与f(x)的变化情况如下表:x1(1,2)2f′(x)-0+f(x)1-ln2极小值0-+ln2∴在上,当x=1时,f(x)取得极小值,也是最小值,且f(1)=0.又f=1-ln2,f(2)=-+ln2,∴f-f(2)=-2ln2=×(3-4ln2)=ln>0,∴f>f(2),∴f(x)在上的最大值为f=1-ln2,最小值为f(1)=0.由函数的最值求参数[典例] 已知函数f(x)=ax3-6ax2+b,x∈[-1,2]的最大值为3,最小值为-29.求a,b的值.[解] 由题设知a≠0,否则f(x)=b为常数函数,与题设矛盾.求导得f′(x)=3ax2-12ax=3ax(x-4),令f′(x)=0,得x1=0,x2=4(舍去).当a>0,且x变化时,f′(x),f(x)的变化情况如下表:x-1(-1,0)0(0,2)2f′(x)+0-f(x)-7a+bb-16a+b由表可知,当x=0时f(x)取得极大值b,也就是函数在[-1,2]上的最大值,∴f(0)=nb=3.又f(-1)=-7a+3,f(2)=-16a+3<f(-1),∴f(2)=-16a+3=-29,解得a=2.当a<0时,同理可得,当x=0时,f(x)取得极小值b,也就是函数在[-1,2]上的最小值,∴f(0)=b=-29.又f(-1)=-7a-29,f(2)=-16a-29>f(-1),∴f(2)=-16a-29=3,解得a=-2.综上可得,a=2,b=3或a=-2,b=-29.已知函数最值求参数的步骤(1)求出函数在给定区间上的极值及函数在区间端点处的函数值;(2)通过比较它们的大小,判断出哪个是最大值,哪个是最小值;(3)结合已知求出参数,进而使问题得以解决. [活学活用]已知函数f(x)=4x+(x>0,a>0)在x=3时取得最小值,求a的值.解:由题意知f′(x)=4-=.又x>0,a>0,令f′(x)=0,得x=,当0<x<时,f′(x)<0;当x>时,f′(x)>0.故f(x)在上单调递减,在上单调递增,即当x=时,f(x)取得最小值,则=3,解得a=36.与最值有关的恒成立问题[典例] 已知函数f(x)=x3+ax2+bx+c在x=-与x=1处都取得极值.(1)求a,b的值及函数f(x)的单调区间.(2)若x∈[-1,2],不等式f(x)
f(2)=2+c,解得c<-1或c>2.故c的取值范围为(-∞,-1)∪(2,+∞).[一题多变]1.[变设问]若本例中条件不变,把(2)中“x∈[-1,2],不等式f(x)c-,所以f(1)=c-为最小值.因为存在x∈[-1,2],不等式f(x)f(1)=c-,即2c2-2c+3>0,解得c∈R.2.[变条件,变设问]已知函数f(x)=x3+ax+b(a,b∈R)在x=2处取得极小值-.(1)求f(x)的单调递增区间.n(2)若f(x)≤m2+m+在[-4,3]上恒成立,求实数m的取值范围.解:(1)f′(x)=x2+a,由f′(2)=0,得a=-4;再由f(2)=-,得b=4.所以f(x)=x3-4x+4,f′(x)=x2-4.令f′(x)=x2-4>0,得x>2或x<-2.所以f(x)的单调递增区间为(-∞,-2),(2,+∞).(2)因为f(-4)=-,f(-2)=,f(2)=-,f(3)=1,所以函数f(x)在[-4,3]上的最大值为.要使f(x)≤m2+m+在[-4,3]上恒成立,只需m2+m+≥,解得m≥2或m≤-3.所以实数m的取值范围是(-∞,-3]∪[2,+∞).恒成立问题向最值转化的方法(1)要使不等式f(x)f(x)max,则上面的不等式恒成立.(2)要使不等式f(x)>h在区间[m,n]上恒成立,可先在区间[m,n]上求出函数f(x)的最小值f(x)min,只要f(x)min>h,则不等式f(x)>h恒成立. 层级一 学业水平达标1.设函数f(x)=2x+-1(x<0),则f(x)( )A.有最大值 B.有最小值C.是增函数D.是减函数解析:选A f′(x)=2-=,令f′(x)=0,得x=-.n当x<-时,f′(x)>0;当-<x<0时,f′(x)<0,∴x=-是函数f(x)的极大值点,也是最大值点.故f(x)有最大值,无最小值.2.函数y=2x3-3x2-12x+5在[-2,1]上的最大值、最小值分别是( )A.12,-8B.1,-8C.12,-15D.5,-16解析:选A y′=6x2-6x-12,由y′=0⇒x=-1或x=2(舍去).x=-2时,y=1;x=-1时,y=12;x=1时,y=-8.∴ymax=12,ymin=-8.故选A.3.函数f(x)=2+,x∈(0,5]的最小值为( )A.2B.3C.D.2+解析:选B 由f′(x)=-==0,得x=1,且x∈(0,1)时,f′(x)<0,x∈(1,5]时,f′(x)>0,∴x=1时,f(x)最小,最小值为f(1)=3.4.函数f(x)=x4-4x(|x|<1)( )A.有最大值,无最小值B.有最大值,也有最小值C.无最大值,有最小值D.既无最大值,也无最小值解析:选D f′(x)=4x3-4=4(x-1)(x2+x+1).令f′(x)=0,得x=1.又x∈(-1,1)且1∉(-1,1),∴该方程无解,故函数f(x)在(-1,1)上既无极值也无最值.故选D.5.函数y=x+2cosx在上取最大值时,x的值为( )A.0B.C.D.n解析:选B y′=1-2sinx,令y′=0,得sinx=,∵x∈,∴x=.由y′>0得sinx<,∴0≤x<;由y′<0得sinx>,∴2>,∴当x=时取最大值,故应选B.6.函数f(x)=x2-(x<0)的最小值是________.解析:f′(x)=2x+.令f′(x)=0,得x=-3.当x<-3时,f′(x)<0;当-3<x<0时,f′(x)>0.所以当x=-3时,f(x)取得极小值,也是最小值,所以f(x)min=27.答案:277.函数f(x)=xe-x,x∈[0,4]的最小值为________.解析:f′(x)=e-x-xe-x=e-x(1-x).令f′(x)=0,得x=1(e-x>0),∴f(1)=>0,f(0)=0,f(4)=>0,所以f(x)的最小值为0.答案:08.若函数f(x)=x3-3x-a在区间[0,3]上的最大值、最小值分别为m,n,则m-n=________.解析:∵f′(x)=3x2-3,∴当x>1或x<-1时,f′(x)>0;当-1<x<1时,f′(x)<0.∴f(x)在[0,1]上单调递减,在[1,3]上单调递增.n∴f(x)min=f(1)=1-3-a=-2-a=n.又∵f(0)=-a,f(3)=18-a,∴f(0)<f(3).∴f(x)max=f(3)=18-a=m,∴m-n=18-a-(-2-a)=20.答案:209.已知k为实数,f(x)=(x2-4)(x+k).(1)求导函数f′(x);(2)若x=-1是函数f(x)的极值点,求f(x)在区间[-2,2]上的最大值和最小值.解:(1)∵f(x)=x3+kx2-4x-4k,∴f′(x)=3x2+2kx-4.(2)由f′(-1)=0,得k=-.∴f(x)=x3-x2-4x+2,f′(x)=3x2-x-4.由f′(x)=0,得x=-1或x=.又f(-2)=0,f(-1)=,f=-,f(2)=0,∴f(x)在区间[-2,2]上的最大值为,最小值为-.10.已知函数f(x)=x3+ax2+bx+5,曲线y=f(x)在点P(1,f(1))处的切线方程为y=3x+1.(1)求a,b的值;(2)求y=f(x)在[-3,1]上的最大值.解:(1)依题意可知点P(1,f(1))为切点,代入切线方程y=3x+1可得,f(1)=3×1+1=4,∴f(1)=1+a+b+5=4,即a+b=-2,又由f(x)=x3+ax2+bx+5得,又f′(x)=3x2+2ax+b,而由切线y=3x+1的斜率可知f′(1)=3,∴3+2a+b=3,即2a+b=0,由解得∴a=2,b=-4.(2)由(1)知f(x)=x3+2x2-4x+5,nf′(x)=3x2+4x-4=(3x-2)(x+2),令f′(x)=0,得x=或x=-2.当x变化时,f(x),f′(x)的变化情况如下表:x-3(-3,-2)-21f′(x)+0-0+f(x)8极大值极小值4∴f(x)的极大值为f(-2)=13,极小值为f=,又f(-3)=8,f(1)=4,∴f(x)在[-3,1]上的最大值为13.层级二 应试能力达标1.函数f(x)=在区间[2,4]上的最小值为( )A.0 B.C.D.解析:选C f′(x)==,当x∈[2,4]时,f′(x)<0,即函数f(x)在[2,4]上是单调递减函数,故当x=4时,函数f(x)有最小值.2.函数f(x)=x3-3ax-a在(0,1)内有最小值,则a的取值范围为( )A.[0,1)B.(0,1)C.(-1,1)D.解析:选B ∵f′(x)=3x2-3a,令f′(x)=0,可得a=x2,又∵x∈(0,1),∴0<a<1,故选B.3.若函数f(x)=x3-3x2-9x+k在区间[-4,4]上的最大值为10,则其最小值为( )A.-10B.-71C.-15D.-22n解析:选B f′(x)=3x2-6x-9=3(x-3)(x+1).由f′(x)=0,得x=3或x=-1.又f(-4)=k-76,f(3)=k-27,f(-1)=k+5,f(4)=k-20.由f(x)max=k+5=10,得k=5,∴f(x)min=k-76=-71.4.已知当x∈时,函数f(x)=tx-sinx(t∈R)的值恒小于零,则t的取值范围是( )A.B.C.D.解析:选A f(x)=tx-sinx<0在x∈内恒成立,即t<在内恒成立.令g(x)=,则g′(x)=.令φ(x)=xcosx-sinx,则φ′(x)=-xsinx,当x∈时,φ′(x)<0,∴φ(x)在上单调递减,∴φ(x)<φ(0)=0,∴sinx>xcosx,∴g′(x)<0,∴g(x)在内单调递减,∴t≤=.5.设函数f(x)=x2ex,若当x∈[-2,2]时,不等式f(x)>m恒成立,则实数m的取值范围是________.解析:f′(x)=xex+x2ex=·x(x+2),由f′(x)=0得x=0或x=-2.当x∈[-2,2]时,f′(x),f(x)随x的变化情况如下表:x-2(-2,0)0(0,2)2f′(x)0-0+f(x)02e2n∴当x=0时,f(x)min=f(0)=0,要使f(x)>m对x∈[-2,2]恒成立,只需m<f(x)min,∴m<0.答案:(-∞,0)6.已知函数y=-x2-2x+3在区间[a,2]上的最大值为,则a=________.解析:y′=-2x-2,令y′=0,得x=-1,∴函数在(-∞,-1)上单调递增,在(-1,+∞)上单调递减.若a>-1,则最大值为f(a)=-a2-2a+3=,解得a=-;若a≤-1,则最大值为f(-1)=-1+2+3=4≠.综上知,a=-.答案:-7.已知函数f(x)=ax3+x2+bx(其中常数a,b∈R),g(x)=f(x)+f′(x)是奇函数.(1)求f(x)的表达式;(2)求g(x)在区间[1,2]上的最大值与最小值.解:(1)∵f′(x)=3ax2+2x+b,∴g(x)=f(x)+f′(x)=ax3+(3a+1)x2+(b+2)x+b.∵g(x)是奇函数,∴g(-x)=-g(x),从而3a+1=0,b=0,解得a=-,b=0,因此f(x)的表达式为f(x)=-x3+x2.(2)由(1)知g(x)=-x3+2x,∴g′(x)=-x2+2,令g′(x)=0.解得x1=-(舍去),x2=,而g(1)=,g()=,g(2)=,n因此g(x)在区间[1,2]上的最大值为g()=,最小值为g(2)=.8.已知函数f(x)=lnx+.(1)当a<0时,求函数f(x)的单调区间;(2)若函数f(x)在[1,e]上的最小值是,求a的值.解:函数f(x)=lnx+的定义域为(0,+∞),f′(x)=-=,(1)∵a<0,∴f′(x)>0,故函数在其定义域(0,+∞)上单调递增.(2)x∈[1,e]时,分如下情况讨论:①当a<1时,f′(x)>0,函数f(x)单调递增,其最小值为f(1)=a<1,这与函数在[1,e]上的最小值是相矛盾;②当a=1时,函数f(x)在[1,e]上单调递增,其最小值为f(1)=1,同样与最小值是相矛盾;③当10,f(x)单调递增,所以,函数f(x)的最小值为f(a)=lna+1,由lna+1=,得a=.④当a=e时,函数f(x)在[1,e]上有f′(x)<0,f(x)单调递减,其最小值为f(e)=2,这与最小值是相矛盾;⑤当a>e时,显然函数f(x)在[1,e]上单调递减,其最小值为f(e)=1+>2,仍与最小值是相矛盾;综上所述,a的值为.