云南省泸西县中枢镇2018中考数学复习第六章圆讲义

云南省泸西县中枢镇2018中考数学复习第六章圆讲义

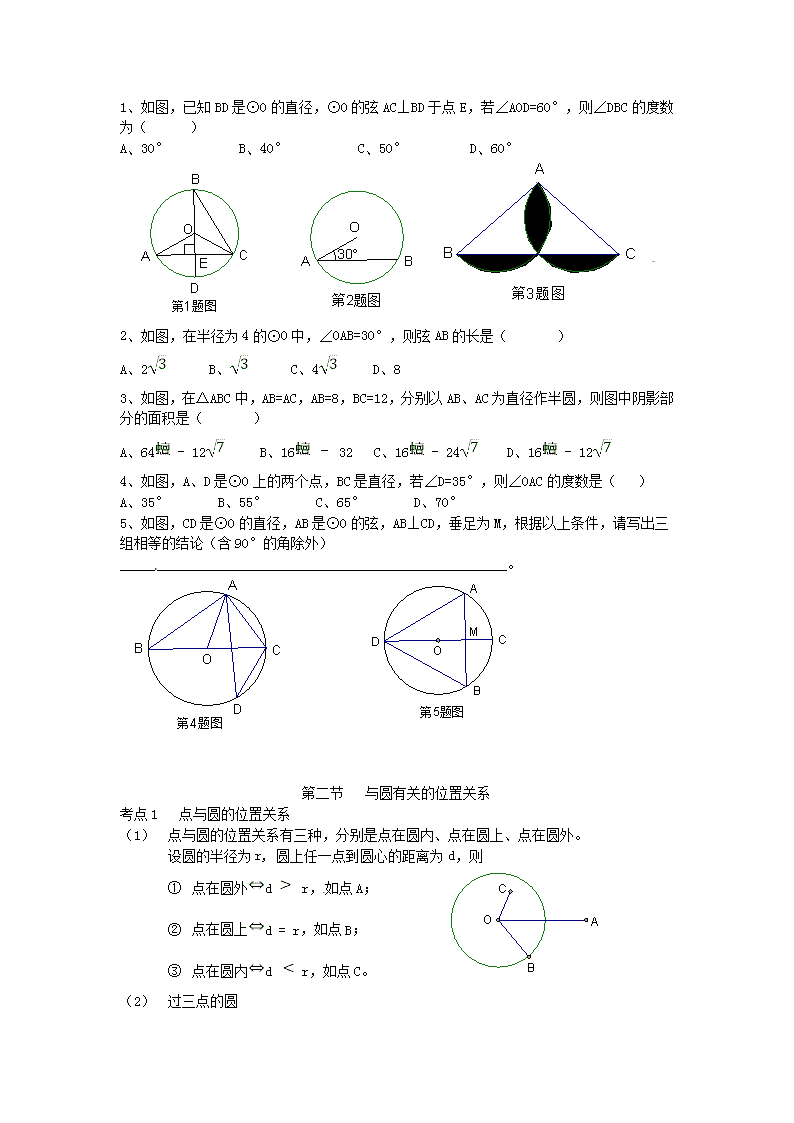
第六章圆第一节圆的基本性质考点1圆的有关概念（1）平面上到定点的距离等于定长的所有点组成的图形叫做圆，其中定点叫做圆心，定长叫做半径。（2）圆上任意两点间的部分叫做弧；小于半圆的弧叫劣弧；大于半圆的弧叫做优弧。（3）连接圆上任意两点的线段叫做弦；经过圆心的弦叫做直径；直径是圆内最长的弦；直径等于半径的二倍。（4）顶点在圆心的角，叫做圆心角。（5）顶点在圆上，并且两边分别和圆相交，这样的角叫做圆周角。（6）三角形的三个顶点确定一个圆，这个圆叫做三角形的外接圆，外接圆的圆心是三角形三条边垂直平分线的交点，叫做三角形的外心。（7）和三角形的三边都相切的圆，叫做三角形的内切圆，内切圆的圆心是三角形三条角平分线的交点，叫做三角形的内心。考点2圆的有关性质（1）圆是轴对称图形；其对称轴是经过圆心的任意一条直线。（2）圆也是中心对称图形，圆心是它的对称中心。（3）圆心确定圆的位置，半径确定圆的大小；不在同一直线上的三点确定一个圆。考点3垂径定理及推论定理垂直于弦的直径平分弦，并且平分弦所对的两条弧推论推论1（1）平分弦（不是直径）的直径垂直于弦，并且平分弦所对的两条弧（2）弦的垂直平分线经过圆心，并且平分弦所对的两条弧推论2圆的两条平行弦所夹的弧相等。推论3过圆心；平分弦；垂直于弦；平分弦所对的劣弧；平分弦所对的优弧，若一条直线具备这五项中任意两项，则必具备另外三项。考点4弧、弦、弦心距、圆心角的关系定理：在同圆或等圆中，相等的圆心角所对的弧相等，所对的弦也相等，所对弦的弦心距相等。推论：（1）在同圆或等圆中，如果两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等，那么其他各组量也分别对应相等。（2）弧的度数等于它所对的圆心角的度数。【温馨提示】应用定理时一定注意“在同圆或等圆中”的条件；同时要特别注意一条弦是对着两条弧的。考点5圆周角定理及其推论定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半。推论：半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径。习题精编n1、如图，已知BD是⊙O的直径，⊙O的弦AC⊥BD于点E，若∠AOD=60°，则∠DBC的度数为（）A、30°B、40°C、50°D、60°2、如图，在半径为4的⊙O中，∠OAB=30°，则弦AB的长是（）A、2B、C、4D、83、如图，在△ABC中，AB=AC，AB=8，BC=12，分别以AB、AC为直径作半圆，则图中阴影部分的面积是（）A、64-12B、16–32C、16-24D、16-124、如图，A、D是⊙O上的两个点，BC是直径，若∠D=35°，则∠OAC的度数是（）A、35°B、55°C、65°D、70°5、如图，CD是⊙O的直径，AB是⊙O的弦，AB⊥CD，垂足为M，根据以上条件，请写出三组相等的结论（含90°的角除外）_______________________________________________________。第二节与圆有关的位置关系考点1点与圆的位置关系（1）点与圆的位置关系有三种，分别是点在圆内、点在圆上、点在圆外。设圆的半径为r,圆上任一点到圆心的距离为d，则①点在圆外dr，如点A；②点在圆上d=r，如点B；③点在圆内dr，如点C。（2）过三点的圆n经过三点的圆①经过同一直线上的三点不能作圆；②经过不在同一直线上的三点，有且只有一个圆。三角形的外心经过三角形各顶点的圆叫做三角形的外接圆；外接圆的圆心叫做三角形的外心，这个三角形叫做这个圆的内接三角形。三角形外接圆的作法①确定外心：作任意两边的中垂线，交点即为外心；②确定半径：两边中垂线的交点到三角形任意一个顶点的距离作为半径；考点2直线与圆的位置关系设圆的半径为r，一个点到圆心的距离为d。直线与圆的位置关系d与r的关系交点的个数示意图相离dr没有公共点相切d=r有且只有一个公共点相交dr有两个公共点考点3圆与圆的位置关系圆与圆的位置关系考点4切线的性质与判定第三节与圆有关的计算考点1与垂径定理有关的计算内容公式提示n如图，⊙O的半径OD与弦AB垂直，用r表示圆的半径、a表示弦长、d表示弦心距、h表示弓形高。（1）r=d+h（2）=(+=(+((3)sin∠AOD=(4)cos∠AOD=遇到弦、半径、圆心角相关的问题时，一般添加弦心距、弦的一半、圆心角的一半、弦心距可集中在如图所示的Rt△AOC中考点2弧与面积的计算圆周长C=2πr或C=πd(1)r为圆半径(2)n为圆心角所对的圆心角的度数(3)l是扇形的弧长圆的弧长I=圆面积S=π扇形面积S=或S=lr考点3圆柱、圆锥的侧面积圆柱=2πrh=2πrh+2π(1)侧面展开图为矩形(2)r为底面半径，h为圆柱高圆锥=lr=lr+π(1)r底面圆的半径(2)l为母线长，h为圆锥的高【温馨提示】圆锥面积和扇形面积计算公式中l代表的意义不同。习题精编n1、如图，已知圆锥侧面展开图的展开面积为65π,扇形的弧长为10πcm，则圆锥母线长是（）A、5cmB、10cmC、12cmD、13cm2、一个圆锥侧面展开图的扇形的弧长为12π，则这个圆锥底面圆的半径为（）A、6B、12C、24D、23、在Rt△ABC中，∠C=90°，BC=4cm，AC=3cm，把△ABC绕点A顺时针旋转90°后，得到△A，如图所示，则点B所走过的路径长为（）A、5B、πcmC、πcmD、5πcm4、已知：一个圆锥的底面直径为6cm，母线长为8cm，则它的表面积为（）A、24πB、33C、24D、33π5、已知圆锥的底面直径为4，母线长为6，则它的侧面展开图的圆心角为________。6、已知扇形的弧长为20π，所在圆的半径是10，那么这个扇形的面积为_____________。