2019秋九年级数学上册反比例函数6.3反比例函数的应用精练（含2019年新题）

申明敬告： 本站不保证该用户上传的文档完整性，不预览、不比对内容而直接下载产生的反悔问题本站不予受理。

文档介绍

2019秋九年级数学上册反比例函数6.3反比例函数的应用精练（含2019年新题）

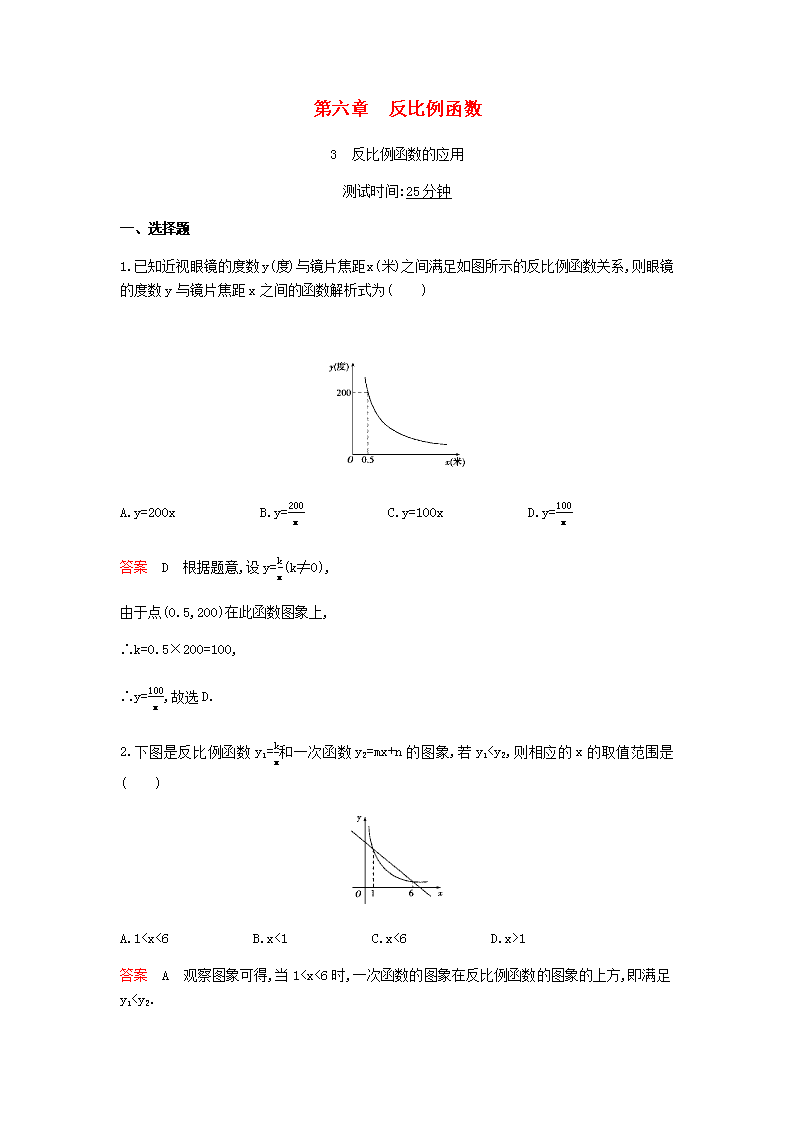
第六章　反比例函数3　反比例函数的应用测试时间:25分钟一、选择题1.已知近视眼镜的度数y(度)与镜片焦距x(米)之间满足如图所示的反比例函数关系,则眼镜的度数y与镜片焦距x之间的函数解析式为(　　)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A.y=200x　　　　　　B.y=200x　　　　　　C.y=100x　　　　　　D.y=100x答案　D　根据题意,设y=kx(k≠0),由于点(0.5,200)在此函数图象上,∴k=0.5×200=100,∴y=100x,故选D.2.下图是反比例函数y1=kx和一次函数y2=mx+n的图象,若y11答案　A　观察图象可得,当10).(2)∵I≤10,I=36R,∴36R≤10,∴R≥3.6,即用电器的可变电阻应控制在3.6Ω及3.6Ω以上的范围内.故填R≥3.6.7.(2019甘肃兰州永登期末)如图,在平面直角坐标系xOy中,已知正比例函数y=12x的图象与反比例函数y=kx的图象交于A(a,-2),B两点.(1)反比例函数的解析式为　　　　,点B的坐标为　　　　; (2)观察图象,直接写出12x-kx<0的解集.n解析　(1)把A(a,-2)代入y=12x,可得a=-4,∴A(-4,-2),把A(-4,-2)代入y=kx,可得k=8,∴反比例函数的表达式为y=8x.∵点B与点A关于原点对称,∴B(4,2).故答案为y=8x;(4,2).(2)由A、B点的坐标和函数图象可知,12x-kx<0的解集是x<-4或0y2时自变量x的取值范围.解析　(1)∵D(2,-3)在函数y2=k2x的图象上,n∴k2=2×(-3)=-6,故y2=-6x.作DE⊥x轴,垂足为E,如图.易知E(2,0),∵D(2,-3),B是线段AD的中点,且OB∥DE,∴O为线段AE的中点,∴A(-2,0),∵A(-2,0),D(2,-3)在函数y1=k1x+b的图象上,∴-2k1+b=0,2k1+b=-3,解得k1=-34,b=-32,∴y1=-34x-32.(2)由y=-34x-32,y=-6x得x=2,y=-3或x=-4,y=32.故点C的坐标为-4,32.∴S△COD=S△AOC+S△AOD=12×2×32+12×2×3=92.(3)当y1>y2时,x的取值范围是x<-4或0
查看更多

相关文章

您可能关注的文档