2019秋九年级数学上册图形的相似4.4探索三角形相似的条件（第2课时）相似三角形的判定定理2精练

2019秋九年级数学上册图形的相似4.4探索三角形相似的条件（第2课时）相似三角形的判定定理2精练

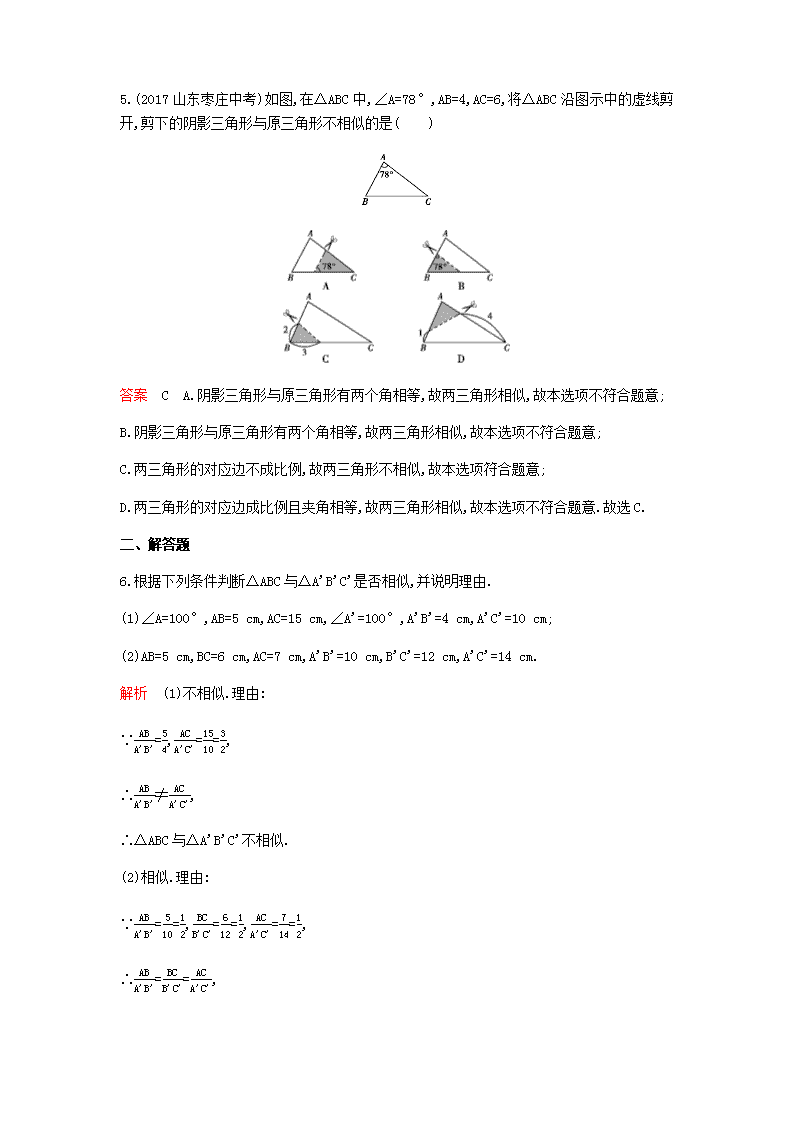
第四章　图形的相似第2课时　相似三角形的判定定理2测试时间:25分钟一、选择题1.(2019天津红桥期末)如图,以A,B,C为顶点的三角形与以D,E,F为顶点的三角形相似,则这两个三角形的相似比为(　　)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　A.2∶1　　　　　　B.3∶1　　　　　　C.4∶3　　　　　　D.3∶2答案　A　∵以A,B,C为顶点的三角形与以D,E,F为顶点的三角形相似,∴ACEF=BCDF=84=126=21,故选A.2.满足下列条件的各对三角形中,相似的两个三角形是(　　)A.∠A=60°,AB=5cm,AC=10cm;∠A'=60°,A'B'=3cm,A'C'=10cmB.∠A=45°,AB=4cm,BC=6cm;∠D=45°,DE=2cm,DF=3cmC.∠C=30°,AB=8cm,BC=4cm;∠E=30°,DF=6cm,FE=3cmD.∠A=∠A',且AB·A'C'=AC·A'B'答案　D　A.∵∠A=60°,AB=5cm,AC=10cm,∠A'=60°,A'B'=3cm,A'C'=10cm,∴∠A=∠A',ABA'B'=53,ACA'C'=1,∴ABA'B'≠ACA'C',∴△ABC和△A'B'C'不相似;B.∵∠A=45°,AB=4cm,BC=6cm,∠D=45°,DE=2cm,DF=3cm,∴∠A=∠D,ABDE=BCDF=2,n但是∠A和∠D不是夹角,∴△ABC和△DEF不相似;C.∵∠C=30°,AB=8cm,BC=4cm,∠E=30°,DF=6cm,FE=3cm,∴ABDF=BCFE=43,但是∠C和∠E不是夹角,∴△ABC和△DFE不相似;D.∵∠A=∠A',且AB·A'C'=AC·A'B',∴AB∶A'B'=AC∶A'C',∴△ABC和△A'B'C'相似.故选D.3.(2018天津河北模拟)下列条件不能判定△ADB∽△ABC的是(　　)A.∠ABD=∠ACB　　　　　B.∠ADB=∠ABC　　　　　C.AB2=AD·AC　　　　　D.ADAC=DBBC答案　D　A.∵∠ABD=∠ACB,∠A=∠A,∴△ADB∽△ABC,故此选项不符合题意;B.∵∠ADB=∠ABC,∠A=∠A,∴△ADB∽△ABC,故此选项不符合题意;C.∵AB2=AD·AC,∴ACAB=ABAD,∵∠A=∠A,∴△ADB∽△ABC,故此选项不符合题意;D.由ADAC=DBBC不能判定△ADB∽△ABC,故此选项符合题意.故选D.4.如图,四边形ABCD的对角线AC、BD相交于点O,且将这个四边形分成①、②、③、④四个三角形.若OA∶OC=OB∶OD,则下列结论中一定正确的是(　　)A.①与②相似　　　　B.①与③相似　　　　C.①与④相似　　　　D.②与④相似答案　B　∵OA∶OC=OB∶OD,∠AOB=∠COD,∴△AOB∽△COD,故选B.n5.(2017山东枣庄中考)如图,在△ABC中,∠A=78°,AB=4,AC=6,将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(　　)答案　C　A.阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;B.阴影三角形与原三角形有两个角相等,故两三角形相似,故本选项不符合题意;C.两三角形的对应边不成比例,故两三角形不相似,故本选项符合题意;D.两三角形的对应边成比例且夹角相等,故两三角形相似,故本选项不符合题意.故选C.二、解答题6.根据下列条件判断△ABC与△A'B'C'是否相似,并说明理由.(1)∠A=100°,AB=5cm,AC=15cm,∠A'=100°,A'B'=4cm,A'C'=10cm;(2)AB=5cm,BC=6cm,AC=7cm,A'B'=10cm,B'C'=12cm,A'C'=14cm.解析　(1)不相似.理由:∵ABA'B'=54,ACA'C'=1510=32,∴ABA'B'≠ACA'C',∴△ABC与△A'B'C'不相似.(2)相似.理由:∵ABA'B'=510=12,BCB'C'=612=12,ACA'C'=714=12,∴ABA'B'=BCB'C'=ACA'C',n∴△ABC∽△A'B'C'.7.如图,在正方形ABCD中,P是BC边上的点,且BP=3PC,Q是CD的中点.求证:△ADQ∽△QCP.证明　设正方形ABCD的边长为4a(a>0),则AD=CD=BC=4a.∵Q是CD的中点,BP=3PC,∴DQ=CQ=2a,PC=a.∴DQCP=ADQC=2.又∵∠D=∠C=90°,∴△ADQ∽△QCP.8.如图所示,A、B、C、P均在边长为1的正方形网格的格点上.(1)判断△PBA与△ABC是否相似,并说明理由;(2)求∠BAC的度数.解析　(1)△PBA与△ABC相似.理由:∵BC=5,PB=1,AB=5,∴PBAB=BABC=55,又∵∠PBA=∠ABC,∴△PBA∽△ABC.(2)由(1)知,△PBA∽△ABC,∴∠BPA=∠BAC,又易知∠BPA=135°,则∠BAC=135°.9.如图,在△ABC中,点D,E分别是△ABC的边AB,AC上的点,且AD=CE=3,AE=6,BD=15,根据以上条件,你认为∠B=∠AED吗?为什么?解析　∠B=∠AED.理由:n因为ADAC=36+3=13,AEAB=615+3=13,且∠A为公共角,所以△AED∽△ABC,所以∠B=∠AED.10.(2016浙江杭州中考)如图,在△ABC中,点D、E分别在AB、AC上,∠AED=∠B.射线AG分别交线段DE、BC于点F、G,且ADAC=DFCG.(1)求证:△ADF∽△ACG;(2)若ADAC=12,求AFFG的值.解析　(1)证明:∵∠AED=∠B,∠DAE=∠CAB,∴△ADE∽△ACB.∴∠ADE=∠C.又∵ADAC=DFCG,∴△ADF∽△ACG.(2)由(1)知△ADF∽△ACG,∴ADAC=AFAG=12,∴AFFG=1.