郡维模拟试卷二--(含答案详解

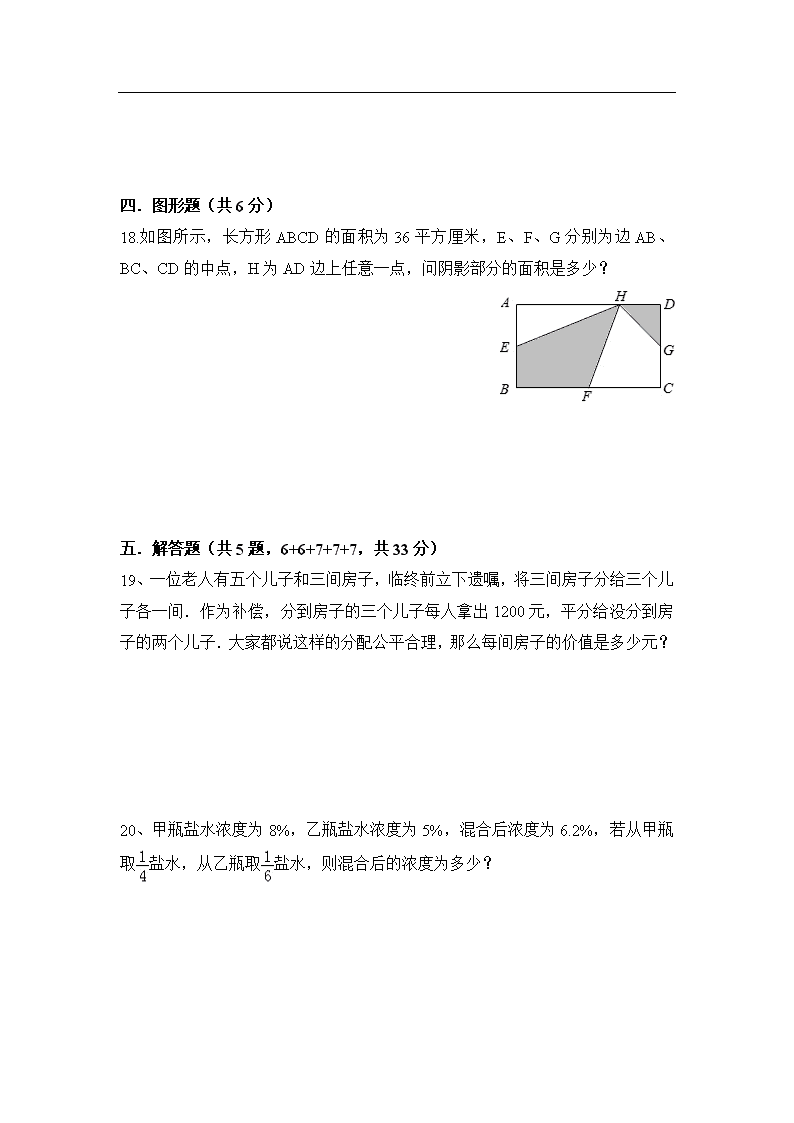
郡维模拟试卷二--(含答案详解

‎2019届JW模拟试卷（二）含答案 姓名： 得分： ‎ 一． 填空题（共10小题，每小题3分，共30分）‎ ‎1．有甲乙两只桶，把甲桶的半桶水倒入空的乙桶，刚好装了乙桶的，再把乙桶里的水倒出全桶的后，还剩15千克，则甲桶可装　 　千克．[来源:学+科+网]‎ ‎2．一条长360米的河堤边等距离植树（两端都要植树）．已挖好每隔4米植一棵树的坑后要改成每隔6米植一棵树，还要挖　 　个坑．‎ ‎3．有3个数字，能组成6个不同的三位数，这6个三位数之和是2886，那么其中最大的三位数是　 　．‎ ‎4．某校六年级原有两个班，现在重新编为三个班，将原一班人数的与原二班人数的组成新一班，将原一班人数的与原二班人数的组成新二班，余下的30人组成新三班．在新三班的人中，原二班的占．原一班有　 　人，二班有　 　人．　‎ ‎5．一种农药，药和水的比值是，现有药5千克，要加水　 　千克．‎ ‎6.平面上5条直线最多能把圆的内部分成　 　部分．‎ ‎7.如果一个三角形的底边长增加20%，底边上的高缩短20%，那么这个新三角形的面积是原来三角形面积的　 　%．‎ ‎8.在一次考试中，甲、乙两人考试结果如下，甲答错了全部试题的，乙答错了7题，甲、乙都答错的试题占全部试题的，那么甲、乙都答对的试题至少有　 　题．‎ ‎9.一种喷洒果树的药水，农药和水的质量比是1：120．现有3千克农药，需要水　 　千克．现要配605千克的药水，需要水　 　千克，需要农药　 　千克．[来源:学科网ZXXK]‎ ‎10.一个表面涂成红色的长方体，分割成棱长为l厘米的小正方体，恰好有3块小正方体的四面是红色的，原长方体的体积是　 　立方厘米．[来源:Zxxk.Com]‎ 二．选择题（共5小题，每小题3分，共15分）‎ ‎11．用100个盒子装杯子，每盒装的个数都不相同，并且每盒不空，那么至少要用（　　）杯子．‎ A．100 B．500 C．1000 D．5050‎ ‎12．小明喝一杯牛奶，第一次喝了一半后，加满水；第二次又喝了一半后，又加满水，最后全部喝完．他喝的牛奶与水比较（　　）‎ A．牛奶多 B．水多 C．一样多 ‎13．电影院第一排有m个座位，后面每一排比前一排多1个座位．第n排的座位数是（　　）‎ A．n个 B．m+n个 C．m+n﹣1个 ‎14．甲数的50%与乙数的相等（甲数、乙数均不为0）则甲数（　　）乙数．‎ A．＞ B．＜ C．= D．无法确定 ‎15．一筐苹果，2个2个地拿，3个3个地拿，4个4个地拿，5个5个地拿都正好拿完没有余数，这筐苹果最少应有（　　）个．‎ A．120 B．90 C．60 D．30‎ 三．计算题（共16分）‎ ‎16．解方程．（每小题4分，共8分）‎ ‎0.75×3﹣3x=0.06 7（x+6）﹣3x=4（2x+5）‎ ‎17．简便运算（每小题4分，共8分）‎ ‎（1）4.38﹣2.85+3.62﹣5.15 （2）0.25×1.9×0.5×4‎ ‎[来源:学。科。网]‎ 四．图形题（共6分）‎ ‎18.如图所示，长方形ABCD的面积为36平方厘米，E、F、G分别为边AB、BC、CD的中点，H为AD边上任意一点，问阴影部分的面积是多少？‎ 五．解答题（共5题，6+6+7+7+7，共33分）‎ ‎19、一位老人有五个儿子和三间房子，临终前立下遗嘱，将三间房子分给三个儿子各一间．作为补偿，分到房子的三个儿子每人拿出1200元，平分给没分到房子的两个儿子．大家都说这样的分配公平合理，那么每间房子的价值是多少元？‎ ‎　‎ ‎20、甲瓶盐水浓度为8%，乙瓶盐水浓度为5%，混合后浓度为6.2%，若从甲瓶取盐水，从乙瓶取盐水，则混合后的浓度为多少？‎ ‎[来源:Z*xx*k.Com]‎ ‎21、28名师生去公园划船，恰好坐满了大、小船共5只．大船每只坐6人，小船每只坐4人，一共租了多少只小船？‎ ‎22.甲、乙两人共有人民币存款若干元，甲占两人存款总数的，若乙给甲40元，则甲、乙两人存款的钱数相等．问甲、乙两人原来各有存款多少元？‎ ‎23.一辆公共汽车和一辆小汽车同时从相距450千米的两地相向而行，公共汽车每小时行40千米，小汽车每小时行50千米，几小时后两车相距90千米？（两种情况都解答）‎ ‎2019届JW模拟试卷（二）‎ 参考答案与试题解析 ‎　一．填空题.‎ ‎1．有甲乙两只桶，把甲桶的半桶水倒入空的乙桶，刚好装了乙桶的，再把乙桶里的水倒出全桶的后，还剩15千克，则甲桶可装　　千克．‎ ‎【分析】甲桶的半桶水即甲桶的倒入空的乙桶后，刚好装了乙桶的，则甲桶的容量是乙桶的=，再把乙桶里的水倒出全桶的后，还剩15千克，则乙桶的容量为15÷（﹣）=千克，则甲桶可装水×=千克．‎ ‎【解答】解：[15÷（﹣）]×（）‎ ‎=[15]×，‎ ‎=×，‎ ‎=360（千克）．‎ 答：甲桶可装千克．‎ 故答案为：．‎ ‎　‎ ‎2．一条长360米的河堤边等距离植树（两端都要植树）．已挖好每隔4米植一棵树的坑后要改成每隔6米植一棵树，还要挖　30　个坑．‎ ‎【分析】先求出6和4的最小公倍数12，求出已经挖的坑里面公共的坑的个数360÷12+1=31个，而当每隔6米植一棵树时，需要挖360÷6+1=61个坑，所以还要挖坑的个数是61﹣31=30个．‎ ‎【解答】解：因为6和4的最小公倍数12，‎ 还要挖坑的个数：（360÷6+1）﹣（360÷12+1），‎ ‎=61﹣31，‎ ‎=30（个），‎ 答：还要挖30个坑．‎ 故答案为：30．‎ ‎【点评】关键是利用6和4的最小公倍数，求出已经挖的坑里面公共的坑的个数，进而解决问题．‎ ‎　‎ ‎3．有3个数字，能组成6个不同的三位数，这6个三位数之和是2886，那么其中最大的三位数是　931　．‎ ‎【分析】方法一：设三个数分别为X，Y，Z，这6个三位数分别为100X+10Y+Z、100X+10Z+Y、100Y+10X+Z、100Y+10Z+X、100Z+10X+Y、100Z+10Y+X，然后根据题意列出方程．‎ 方法二：因为6个三位数之和是2886，所以可能求出一个三位数数字的和，进而求出各个数字的和，由此得出答案．‎ ‎【解答】解：设三个数分别为X，Y，Z，则 ‎（100X+10Y+Z）+（100X+10Z+Y）+（100Y+10X+Z）+（100Y+10Z+X）+（100Z+10X+Y）+（100Z+10Y+X）=2886‎ ‎（100+100+10+10+1+1）X+（10+1+100+100+1+10）Y+（1+10+1+10+100+100）Z=2886‎ ‎ 222X+222Y+222Z=2886‎ ‎ 222（X+Y+Z）=2886‎ ‎ X+Y+Z=13‎ 要求最大，所以百位要越大越好，就是9，十位最大只能是3，个位是1，可知此数最大是931．‎ 方法二：2886÷6=481 ‎ 算出数中位的数量是：4+8+1=13‎ 而13=9+3+1．‎ 所以百位要越大越好，就是9，十位最大只能是3，个位是1，‎ 故答案为：931．‎ ‎【点评】此题用方程解答，比较好理解，解题的关键是表示出这6个三位数，然后根据和是2886列出方程．‎ ‎　‎ ‎5．某校六年级原有两个班，现在重新编为三个班，将原一班人数的与原二班人数的组成新一班，将原一班人数的与原二班人数的组成新二班，余下的30人组成新三班．在新三班的人中，原二班的占．原一班有　40　人，二班有　60　人．‎ ‎【分析】在新三班的30人中，原二班的占，则这30人中原二班的人数有30×=18人，原一班的有30﹣18=12人．又原一班人数中的分入新一班，分入新二班，则新三班中，原一班的人数占原来一班总人数的1﹣﹣，则原来一班有12÷（1﹣﹣）人．同理可求出原二班有多少人．‎ ‎【解答】解：（30﹣30×）÷（1﹣﹣）‎ ‎=（30﹣18）×，‎ ‎=40（人）；‎ ‎30×÷（1﹣﹣）‎ ‎=18，‎ ‎=60（人）．‎ 答：原一班有40人，二班有60人．‎ 故答案为：40，60．‎ ‎　‎ ‎【点评】求出新三班中原一班、二班的人数各有多少人及各占原来人数的分率是完成本题的关键．‎ ‎　‎ ‎5．一种农药，药和水的比值是，现有药5千克，要加水　1500　千克．‎ ‎【分析】根据题意，可得水是药的300倍，所以用药的重量乘以300，求出要加水多少千克即可．‎ ‎【解答】解：因为药和水的比值是，‎ 所以水是药的300倍，‎ ‎5×300=1500（千克）‎ 答：现有药5千克，要加水1500千克．‎ 故答案为：1500．‎ ‎【点评】此题主要考查了比的应用．‎ ‎　‎ ‎6．平面上5条直线最多能把圆的内部分成　16　部分．‎ ‎【分析】根据平面上n条直线最多能把圆的内部分成n（n+1）÷2+1可知，5条直线可以把一个圆内部分分成5×6÷2+1=16部分，依此计算即可得出答案．‎ ‎【解答】解：5×6÷2+1‎ ‎=15+1‎ ‎=16（部分）‎ 答：平面上5条直线最多能把圆的内部分成16部分．‎ 故答案为：16．‎ ‎【点评】本题考查直线与平面的关系，有一定难度，注意本题只考虑圆内部分．‎ ‎　‎ ‎　‎ ‎7．如果一个三角形的底边长增加20%，底边上的高缩短20%，那么这个新三角形的面积是原来三角形面积的　96　%．‎ ‎【分析】设原来的三角形的底为a，高为h，求出这个三角形的面积；然后再把原来的底和高看成单位“1”，新的底是原来的1+20%，新的高是原来的1﹣20%，再求出新的面积，用新的面积除以原来的三角形的面积即可．‎ ‎【解答】解：设原来的三角形的底为a，高为h，那么：‎ 原来三角形的面积是：0.5ah；‎ 三角形的底增加后是：a×（1+20%）=1.2a，‎ 三角形的高缩短后是：h×（1﹣20%）=0.8h，‎ 新三角形的面积是：×1.2a×0.8h=0.48ah，‎ ‎0.48ah÷0.5ah=96%．‎ 答：这个新三角形的面积是原来三角形面积的96%．‎ 故答案为：96．‎ ‎【点评】解答此题的关键是分清单位“1”的区别，找清各自以谁为标准，再把数据设出，根据基本的数量关系求解．‎ ‎　‎ ‎8．在一次考试中，甲、乙两人考试结果如下，甲答错了全部试题的，乙答错了7题，甲、乙都答错的试题占全部试题的，那么甲、乙都答对的试题至少有　10　题．‎ ‎【分析】首先根据甲答错了全部试题的，甲、乙都答错的试题占全部试题的，可得全部试题的数量是3、7的公倍数，所以全部试题最少有21题；然后把全部试题的数量看作单位“1”，根据分数乘法的意义，用全部试题的数量乘，求出甲、乙都答错的有3题；再根据分数乘法的意义，用全部试题的数量乘，求出甲一共答错了多少题；最后用全部试题的数量减去甲、乙答错的试题的数量，以及甲答错而乙答对的试题的数量，以及乙答错而甲答对的试题的数量，求出甲、乙都答对的试题至少有多少题即可．‎ ‎【解答】解：因为甲答错了全部试题的，甲、乙都答错的试题占全部试题的，‎ 所以全部试题的数量是3、7的公倍数，‎ 所以全部试题最少有：3×7=21（题）‎ 甲、乙都答错的试题有：21×=3（题）‎ 甲答错的试题有：21×=7（题）‎ 甲、乙都答对的试题至少有：‎ ‎21﹣3﹣（7﹣3）﹣（7﹣3）‎ ‎=21﹣3﹣4﹣4‎ ‎=10（题）‎ 答：甲、乙都答对的试题至少有10题．‎ 故答案为：10．‎ ‎【点评】此题主要考查了分数四则复合应用题，要熟练掌握，解答此题的关键是求出甲答错而乙答对的试题的数量，以及乙答错而甲答对的试题的数量各是多少．‎ ‎　‎ ‎9．一种喷洒果树的药水，农药和水的质量比是1：120．现有3千克农药，需要水　360　千克．现要配605千克的药水，需要水　600　千克，需要农药　5　千克．‎ ‎【分析】由农药和水的比是1：120可知；农药占1份，水占120份，求3千克农药，需要加水多少千克，用3÷1×120计算解答；‎ 由1+120=121，求出药和水的总份数，那农药和水占配成农药的几分之几也可以求出，把农药的总重看作单位“1”，根据一个数乘分数的意义，解答即可．‎ ‎【解答】解：3÷1×120‎ ‎=3×120‎ ‎=360（千克）‎ ‎1+120=121 农药：605×=5（千克） 水：605×=600（千克） ‎ 答：需要水360千克．现要配605千克的药水，需要水600千克，需要农药5千克．‎ 故答案为：360；600；5．‎ ‎【点评】‎ 本题主要考查比的应用，解答本题是把1：120看成农药占一份，水占120份．‎ ‎　‎ ‎10．一个表面涂成红色的长方体，分割成棱长为l厘米的小正方体，恰好有3块小正方体的四面是红色的，原长方体的体积是　5　立方厘米．‎ ‎【分析】根据长方体的特征：6个面都是长方形（特殊情况有两个相对的面是正方形），相对的面的面积相等．把一个表面涂成红色的长方体，分割成棱长为l厘米的小正方体，恰好有3块小正方体的四面是红色的，这个长方体的长应该是5厘米、宽是1厘米、高是1厘米，这样长方体可以分割成5个棱长为1厘米的小正方体，两段的两块五面是红色，中间的3块四面是红色．‎ ‎【解答】解：如图：‎ 根据分析知：这个长方体的长应该是5厘米、宽是1厘米、高是1厘米，这样长方体可以分割成5个棱长为1厘米的小正方体，两段的两块五面是红色，中间的3块四面是红色．‎ 这个长方体的体积是：5×1×1=5（立方厘米）；‎ 答：原来长方体的体积是5立方厘米．‎ 故答案为：5．‎ ‎【点评】此题考查的目的是掌握长方体的特征、长方体的体积计算方法．‎ 二、选择题 ‎　11．用100个盒子装杯子，每盒装的个数都不相同，并且每盒不空，那么至少要用（　　）杯子．‎ A．100 B．500 C．1000 D．5050‎ ‎【分析】用100个盒子装杯子，每盒装的个数都不相同，并且盒盒不空，所以又100种不同的装法，要求至少需要多少个杯子，那么可以从最少的个数装起：即每个盒子里的杯子数分别为1、2、3、4、5、6…100，由此可得出所需要的杯子数为：1+2+3+4+5+…+100，利用高斯求和的方法即可解决问题．‎ ‎【解答】解：根据题干分析可得：每个盒子里的杯子数分别为1、2、3、4、5、6…100，‎ 所以需要的杯子数为：1+2+3+4+5+…+100，‎ ‎=（1+100）×（100÷2），‎ ‎=101×50，‎ ‎=5050（个），‎ 故选：D．‎ ‎　‎ ‎12．小明喝一杯牛奶，第一次喝了一半后，加满水；第二次又喝了一半后，又加满水，最后全部喝完．他喝的牛奶与水比较（　　）‎ A．牛奶多 B．水多 C．一样多 ‎【分析】这一过程中，一直没有加牛奶，最后全部喝完，所以共喝了一杯牛奶，又前后共加两半杯水，+=1，则共喝了一杯水，所以喝的牛奶与水一样多．‎ ‎【解答】解：+=1，则共喝了一杯水，‎ 所以喝的牛奶与水一样多．‎ 故选：C．‎ ‎　‎ ‎13．电影院第一排有m个座位，后面每一排比前一排多1个座位．第n排的座位数是（　　）‎ A．n个 B．m+n个 C．m+n﹣1个 ‎【分析】第1排m个，第2排（m+1）个，第3排（m+2）个，…，从而找到规律，求出第n排的座位．‎ ‎【解答】解：根据题意得：第n排有（m+n﹣1）个座位．‎ 故选：C．　‎ ‎14．甲数的50%与乙数的相等（甲数、乙数均不为0）则甲数（　　）乙数．‎ A．＞ B．＜ C．= D．无法确定 ‎【分析】甲数的50%与乙数的相等，则甲数与乙数的比为：50%=4：5，所以甲数＜乙数．‎ ‎【解答】解：甲数：乙数=：50%=4：5，‎ 所以甲数＜乙数．‎ 故选：B．‎ ‎　　‎ ‎15．一筐苹果，2个2个地拿，3个3个地拿，4个4个地拿，5个5个地拿都正好拿完没有余数，这筐苹果最少应有（　　）个．‎ A．120 B．90 C．60 D．30‎ ‎【分析】一筐苹果，2个2个地拿，3个3个地拿，4个4个地拿，5个5个地拿都正好拿完而没有余数，说明这框苹果是2、3、4、5的倍数，因为4是2的倍数，只要是3、4、5的倍数就一定也是2的倍数，所以只要求出3、4、5的最小公倍数，即可得解．‎ ‎【解答】解：3、4、5互质，所以3、4、5的最小公倍数是3×4×5=60（个），‎ 答：这筐苹果最少应有60个；‎ 故选：C．‎ 二、计算题。‎ ‎16．解方程．‎ ‎0.75×3﹣3x=0.06 ‎ ‎7（x+6）﹣3x=4（2x+5）‎ ‎【分析】利用等式的等式基本性质解方程．‎ ‎【解答】解：0.75×3﹣3x=0.06‎ ‎ 2.25﹣3X=0.06，‎ ‎ 2.25﹣3x+3X=0.06+3X，‎ ‎ 0.06+3X=2.25，‎ ‎ 0.06+3X﹣0.06=2.25﹣0.06，‎ ‎ 3X=2.19，‎ ‎ 3x÷3=2.19÷3，‎ ‎ X=0.73；‎ ‎7（x+6）﹣3x=4（2x+5）‎ ‎ 7X+42﹣3X=8X+20，‎ ‎ 4X+42=8X+20，‎ ‎ 4X+42﹣4X=8X+20﹣4X，‎ ‎ 4X+20=42，‎ ‎ 4X﹣20=42﹣20，‎ ‎ 4X=22，‎ ‎ 4X÷4=22÷4，‎ ‎ X=5.5．‎ ‎【点评】本题主要考查解方程，注意解方程的格式．‎ ‎　‎ ‎17．简便运算 ‎（1）4.38﹣2.85+3.62﹣5.15‎ ‎（2）0.25×1.9×0.5×4．‎ ‎【分析】（1）4.38﹣2.85+3.62﹣5.15，根据加、减法的运算性质进行简算；‎ ‎（2）0.25×1.9×0.5×4．运用乘法交换律和结合律进行简算．‎ ‎【解答】解：（1）4.38﹣2.85+3.62﹣5.15，‎ ‎=4.38+3.62﹣（2.85+5.15），‎ ‎=8﹣8，‎ ‎=0；‎ ‎（2）0.25×1.9×0.5×4，‎ ‎=（0.25×4）×（1.9×0.5），‎ ‎=1×0.95，‎ ‎=0.95．‎ ‎【点评】此题考查的目的是运用加、减法的运算性质和乘法的运算定律对小数四则混合运算进行简便计算．‎ ‎　‎ 三、图形题 ‎18.如图所示，长方形ABCD的面积为36平方厘米，E、F、G分别为边AB、BC、CD的中点，H为AD边上任意一点，问阴影部分的面积是多少？‎ ‎【分析】如图，连接HB、HC，根据在三角形中等底同高的性质，三角形BHF与三角形FHC的面积相等，三角形HCG与三角形HGD的面积相等，三角形AEH与三角形EBH的面积相等，所以阴影部分的面积就是长方形ABCD的面积的一半．‎ ‎【解答】解：因为三角形BHF与三角形FHC的面积相等，三角形HCG与三角形HGD的面积相等，三角形AEH与三角形EBH的面积相等，‎ 所以阴影部分的面积为：36÷2=18（平方厘米）；‎ 答：阴影部分的面积是18平方厘米．‎ ‎【点评】本题主要利用在三角形中，等底同高时，面积相等解决问题．‎ 四．　解答题（共6分）‎ ‎19‎ ‎．一位老人有五个儿子和三间房子，临终前立下遗嘱，将三间房子分给三个儿子各一间．作为补偿，分到房子的三个儿子每人拿出1200元，平分给没分到房子的两个儿子．大家都说这样的分配公平合理，那么每间房子的价值是多少元？‎ ‎【分析】根据题意先算出分到房子的三个儿子共拿出的钱数，再根据把这些钱平分给没分到房子的两个儿子，就能算出没分到房子的两个儿子分别得的钱数，进一步求得三间房子共值的钱数，进而求得每间房子的价值即可解决问题．‎ ‎【解答】解：三个儿子共拿出：1200×3=3600（元），‎ 每个儿子应该分得：3600÷2=1800（元），‎ 三间房子共值：1800×5=9000（元），‎ 每间房子值：9000÷3=3000（元）．‎ 答：每间房子的价值是3000元．‎ ‎【点评】解决此题关键是求出三间房子总共的价值，进而求得每间房子的价值．‎ ‎　‎ ‎20、甲瓶盐水浓度为8%，乙瓶盐水浓度为5%，混合后浓度为6.2%，若从甲瓶取盐水，从乙瓶取盐水，则混合后的浓度为　 　．‎ ‎【解答】解：设甲瓶盐水质量为a，乙瓶盐水的质量是b．‎ ‎（8%a+5%b）÷（a+b）=6.2%，‎ 解得：a=b，‎ ‎（a×8%+×5%）÷（a+b）‎ ‎=（a+b）÷（b+b）‎ ‎=（b+b）÷b ‎=b×‎ ‎=6.5%，‎ 答：混合后的浓度为6.5%，‎ 故答案为：6.5%．‎ ‎21、28名师生去公园划船，恰好坐满了大、小船共5只．大船每只坐6人，小船每只坐4人，一共租了　1　只小船．‎ ‎【解答】解：设大船的数量是x只，那么小船的数量就是（5﹣x）只，‎ ‎6x+（5﹣x）×4=28‎ ‎ 6x+20﹣4x=28‎ ‎ 2x+20=28‎ ‎ x=4‎ ‎5﹣4=1（只）‎ 答：一共租了1只小船．‎ 故答案为：1只。‎ ‎22．甲、乙两人共有人民币存款若干元，甲占两人存款总数的，若乙给甲40元，则甲、乙两人存款的钱数相等．问甲、乙两人原来各有存款多少元？‎ ‎【分析】把两人的存款总额看成单位“1”，乙给甲40元，则甲、乙两人存款的钱数相等，此时甲的存款就是总存款的，增加了总存款的（﹣），它对应的数量是40元，由此用除法求出总存款，总存款乘上就是甲原来的存款，进而求出乙原来的存款．‎ ‎【解答】解：40÷（﹣）‎ ‎=40÷‎ ‎=720（元）‎ ‎720×=320（元）‎ ‎720﹣320=400（元）‎ 答：甲原来有存款320元，乙原来有存款400元．‎ ‎【点评】本题的关键是找出单位“1”，并找出单位“1”的几分之几对应的数量，用除法就可以求出单位“1”的量．‎ ‎23‎ ‎．一辆公共汽车和一辆小汽车同时从相距450千米的两地相向而行，公共汽车每小时行40千米，小汽车每小时行50千米，几小时后两车相距多少千米？（两种情况都解答）‎ ‎【分析】（1）先求出没相遇时相距90千米时它们共同行驶的路程，运用路程÷速度和=行驶至相距90千米的时间．‎ ‎（2）两车相遇后又相距90千米即行驶的路程是（450+90）千米运用总路程÷速度和=相距90千米的时间．‎ ‎【解答】解：（1）（450﹣90）÷（40+50），‎ ‎=360÷90，‎ ‎=4（小时）；‎ 答：4小时后两车相距90千米．‎ ‎（2）（450+90）÷（40+50），‎ ‎=540÷90，‎ ‎=6（小时）；‎ 答：6小时后两车相距90千米． ‎ ‎ ‎