六年级下册数学课件-整理与复习（1）_北师大版（2014秋）(共20张PPT)

六年级下册数学课件-整理与复习（1）_北师大版（2014秋）(共20张PPT)

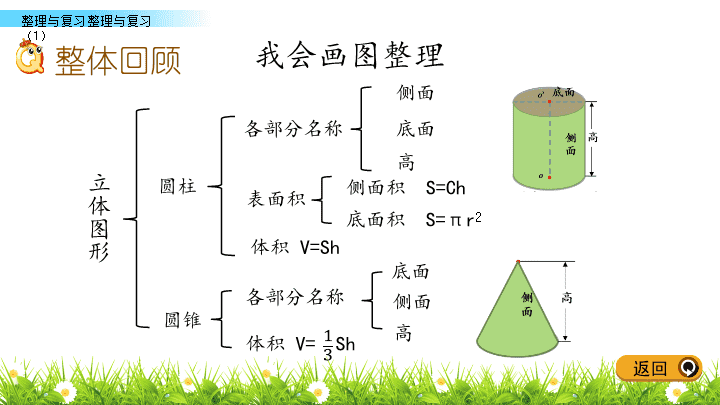
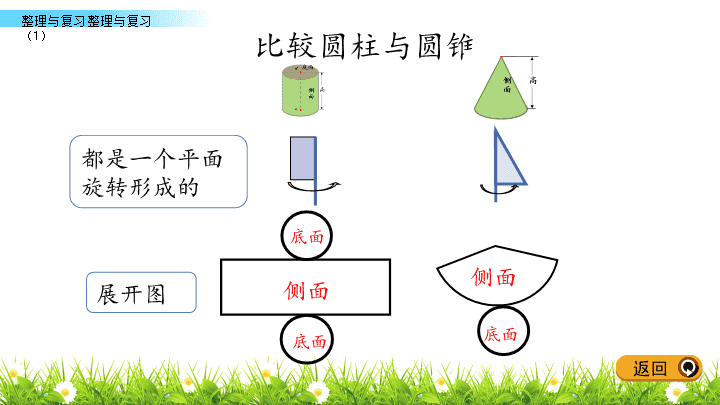
北师大版 数学 六年级 下册 整理与复习 整体回顾 知识梳理 课后作业 综合运用 整理与复习（ 1 ） 立体图形 圆柱 圆锥 各部分名称 侧面 底面 高 表面积 侧面积 S = Ch 底面积 S =π r 2 体积 V = Sh 各部分名称 底面 侧面 高 我会画图整理 体积 V = S h 整体回顾 返回 比较圆柱与圆锥 都是一个平面旋转形成的 展开图 底面 底面 侧面 侧面 底面 返回 比较圆柱与圆锥 圆柱表面积 :S 侧 + 2S 底 圆柱侧面积 :S= C h 圆柱底面积 :S=πr 2 圆锥表面积 :S 扇 +S 底 圆锥侧面积 : 扇形面积 圆锥底面积 :S=πr 2 圆柱体积 : V=Sh 圆锥体积 : V= Sh 返回 底 高 圆 柱 曲面 圆柱有无数条 高 。 1 个侧面 2 个底面 圆 侧面 S 表 ＝ S 侧 +2×πr 2 在 解决实际问题时，并不是所有圆柱都有两个底面，有的有一个，有的没有，要具体问题具体分析。 知识梳理 返回 底面 底面 侧面 ✄ 长 圆柱侧面积 长方形面积 宽 高 底面周长 ＝ ＝ ＝ ＝ × ＝ × 运用 转化 思想，将曲面转化成平面。 返回 圆柱体积＝底面积 × 高 V 圆柱 ＝ πr 2 × h 想一想，怎么用字母来表示呢？ 将未知的问题转化成已知的、已解决的常见问题，可将问题简单化。 返回 圆锥的体积是与它等底等高的圆柱体积的 。 V 圆锥 ＝ ×πr 2 ×h 圆锥体积＝ × 底面积 × 高 返回 上面 一排图形旋转后会得到下面的哪个图形？请连一连。 综合运用 返回 将图形分类，说说图形的名称和特征。 圆 柱 圆 锥 有一个圆圆的底面，一个侧面； 只有一条高 。 有两个 圆圆的 底面，一个侧面；有 无数条高 ；侧面 沿高展开是一个长方形（或正方形） ，长方形的一组邻边等于圆柱的底面周长和高。 返回 判断。（对的画“√”，错的画“ × ” ） 1. 一个三角形沿着一条边旋转一定可以形成一个圆锥。 （ ） 2. 圆柱的侧面展开图不一定是个长方形。 （ ） 3. 圆柱体积是圆锥体积的 3 倍。 （ ） √ × × 圆锥的体积是与它 等底 等高 的 圆柱体积的 。 返回 底面半径 /cm 高 /cm 圆柱 圆锥体积 /cm 3 侧面积 /cm 2 表面积 /cm 2 体积 /cm 3 2 15 6 20 S 表 ＝ 2πrh+2πr 2 V= π r 2 h 188.4 213.52 188.4 62.8 753.6 979.68 2260.8 753.6 V= π r 2 h S 侧 ＝ 2πrh 填表。 返回 圆锥的体积要注意 …… 一个圆锥形谷堆，底面直径为 6m ，高 1.2m 。 （ 1 ）这堆稻谷的体积的多少立方米？ （ 2 ）如果每立方米稻谷的质量为 700kg ，这 堆稻谷的质量为 多 少 千克？ ×3.14× （ 6÷2 ） 2 ×1.2= 答：这堆稻谷的体积的 11.304 立方米。 11.304×700= 答：这堆稻谷的体积的 7912.8kg 。 11.304 （ m 3 ） 7912.8 （ kg ） 返回 用白铁皮制作圆柱形通风管，每节长 80cm ，底面半径 5cm ，制作 20 节这样的通风管，至少需要多大面积的铁皮？ 只有一个侧面 2×3.14×5×80×20= 50240 （ cm 2 ） 答：至少需用 50240cm 2 。 高 底面周长 × × 数量 返回 一块蜂窝煤如图所示。做一块蜂窝煤大约需要用煤多少立方厘米？ 没挖孔的煤的体积 一个孔的体积 一块煤有 12 个孔 一块蜂窝煤的体积 返回 答：做一块蜂窝煤大约要用煤 678.24 立方 厘 米。 1 2 3.14× （ 2÷2 ） 2 ×9=28.26 （ cm 3 ） 28.26×12=339.12 （ cm 3 ） 3 3.14× （ 12÷2 ） 2×9=1017.36 （ cm 3 ） 4 1017.36-339.12=678.24 （ cm 3 ） 返回 如图是我国古代的一种计量时间的仪器沙漏（又称沙钟），它分上下两部分，是根据流沙从上面的容器漏到下面的容器的数量来计量时间的。（单位： cm ） (1) 这时沙漏上部剩余的沙子的体积是多少立方厘米？ 3.14 （ cm 3 ） 答 ：沙漏上部剩余的沙子的体积是 3.14cm 3 。 ×3.14× （ 2÷2 ） 2 ×3= 返回 (2) 这时沙漏下部沙子的体积是多少立方厘米？ 84.78 （ cm 3 ） 84.78 － 10.5975= 74.1825 （ cm 3 ） 答：上部体积是 3.14 立方厘米，下部体积是 74.1825 立方厘米。 ×3.14× （ 6÷2 ） 2 ×9= ×3.14×1.5 2 × （ 9 － 4.5 ） = 10.5975 （ cm 3 ） 如图是我国古代的一种计量时间的仪器沙漏（又称沙钟），它分上下两部分，是根据流沙从上面的容器漏到下面的容器的数量来计量时间的。（单位： cm ） 返回 旋转后得到的立体图形会是什么样呢？ 如图，一个直角梯形绕轴旋转一周后形成的立体图形的体积是多少？ 上面是圆锥 下面是圆柱 实际操作试一试吧！ 返回 课本： 第 60 页第 5 题 课后作业 返回