- 2022-02-12 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级上册数学课件-第八单元第1课时 运用数形结合发现规律 人教版(共15张PPT)
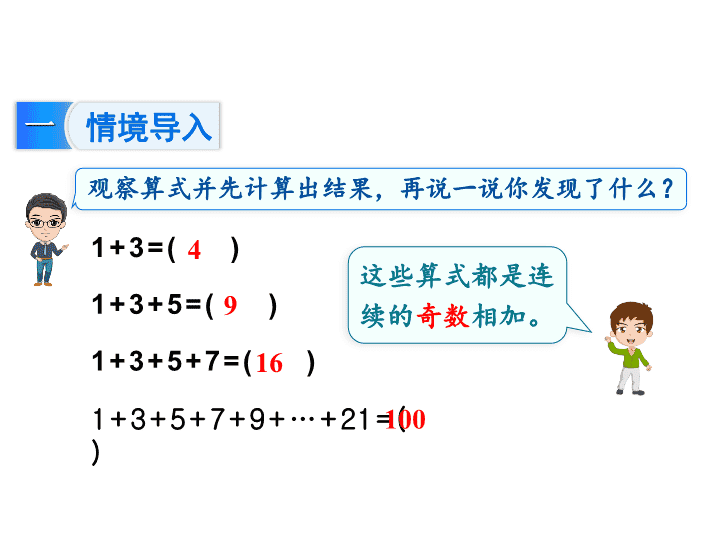
数学广 角 — 数与形 运用数形结合发现规律 8 一 情境导入 观察算式并先计算出结果,再说一说你发现了什么? 1+3= ( ) 1+3+5= ( ) 1+3+5+7= ( ) 1+3+5+7+9+…+ 2 1= ( ) 这些算式都是连续的 奇数 相加。 4 9 16 100 二 新课探究 1 1= ( ) 2 1+3= ( ) 2 1+3+5= ( ) 2 观察一下,上面的图和对应的算式有什么关系?把算式补充完整。 有 1 个 小正方形 每列或每行都 有 2 个 小正方形 每列或每行都 有 3 个 小正方形 1 2 3 ( 教科书第 107 页例 1) 1= ( ) 2 1+3= ( ) 2 1+3+5= ( ) 2 1 2 3 我发现,算式左边的加数是每个正方形图左下角的小正方形和其他“ ” 形图中所包含的小正方形个数之和,正好等于每个正方形图中每行或列小正方形个数的 平方 。 我发现, 从 1 开始的连续奇数的和正好是这串数个数的平方。 1+3= ( ) 2 1+3+5= ( ) 2 1+3+5+7= ( ) 2 1+3+5+7+9+ 1 1+ 1 3+ 1 5+ 1 7+ 1 9= ( ) 2 = 4 = 9 = 1 6 = 10 0 2 3 4 10 ____________________________ = 9 2 你能利用规律直接写一写吗? 1+3+5+7= ( ) 2 1+3+5+7+9+ 11+1 3= ( ) 2 1+3+5+7+9+ 1 1+ 1 3+ 1 5+ 17 4 7 如果遇到困难 , 可以画图来帮助。 算式 图形 每一个图形的个数正好等于从右上角加上其它“ ”形图中所包含的个数。 从 1 开始的连续奇数的和正好是这串数个数的平方。 图形 和 算式 有什么关系? 数形结合 三 随堂练习 请根据 例 1 的结论算一算。 1+3+5+7+5+3+1= ( ) 1+3+5+7+9+ 1 1+ 1 3+ 1 1+9+7+5+3+1= ( ) 25 85 解题思路及方法 ( 教科书第 108 页做一做 ) 1+3+5+7+5+3+1 = 1 6+9 = 2 5 返回 1+3+5+7+9+ 1 1+ 1 3+ 1 1+9+7+5+3+1 = 4 9+ 36 = 8 5 下面每个图中各有多少个红色小正方形和多少个蓝色小正方形? 照这样画下去,第 6 个图形有多少个红色小正方形和多少个蓝色小正方形?第 10 个图形呢?你能解释这其中的道理吗? 6 18 10 26 红色 蓝色 红色 1 2 3 4 … 6 … 10 蓝色 8 10 12 14 … 18 … 26 5 16 n 2 ( n +3 ) 道理: 第 n 个图形 有 n 个红色小正方形, 有 2( n +3) 个蓝色小正方形。 四 培优训练 答:皮球在空中下落的路程一共 有 19.37 5 米。 五 课堂小结 把 图形 与 算式 结合 起来,是发现规律的关键。 从 1 开始的连续几个奇数的和 与正方形数的关系,即有几个连续奇数相加, 每边小正方形个数就是几的平方 。 1. 从课后习题中选取; 2. 完成练习册本课时的习题。 课后作业查看更多