- 2022-02-11 发布 |
- 37.5 KB |
- 3页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级下册数学试题-奥数中的容斥问题 人教版 含解析
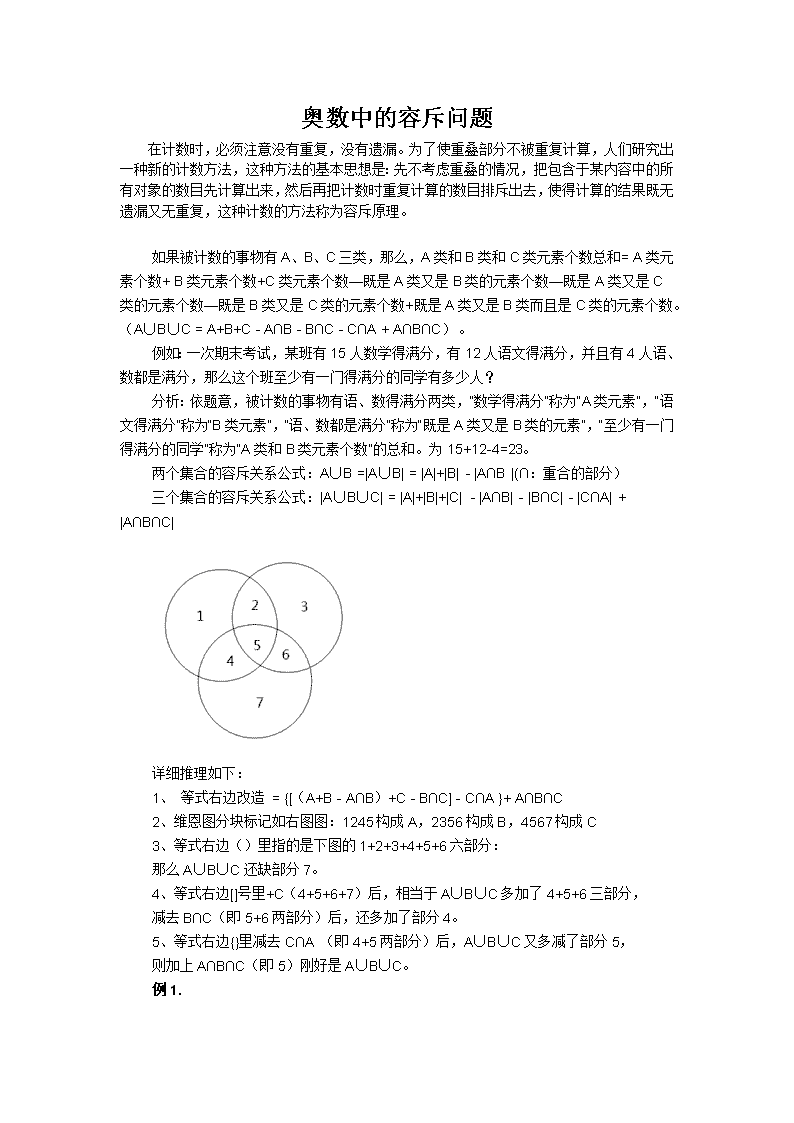
奥数中的容斥问题 在计数时,必须注意没有重复,没有遗漏。为了使重叠部分不被重复计算,人们研究出一种新的计数方法,这种方法的基本思想是:先不考虑重叠的情况,把包含于某内容中的所有对象的数目先计算出来,然后再把计数时重复计算的数目排斥出去,使得计算的结果既无遗漏又无重复,这种计数的方法称为容斥原理。 如果被计数的事物有A、B、C三类,那么,A类和B类和C类元素个数总和= A类元素个数+ B类元素个数+C类元素个数—既是A类又是B类的元素个数—既是A类又是C类的元素个数—既是B类又是C类的元素个数+既是A类又是B类而且是C类的元素个数。(A∪B∪C = A+B+C - A∩B - B∩C - C∩A + A∩B∩C) 。 例如:一次期末考试,某班有15人数学得满分,有12人语文得满分,并且有4人语、数都是满分,那么这个班至少有一门得满分的同学有多少人? 分析:依题意,被计数的事物有语、数得满分两类,“数学得满分”称为“A类元素”,“语文得满分”称为“B类元素”,“语、数都是满分”称为“既是A类又是B类的元素”,“至少有一门得满分的同学”称为“A类和B类元素个数”的总和。为15+12-4=23。 两个集合的容斥关系公式:A∪B =|A∪B| = |A|+|B| - |A∩B |(∩:重合的部分) 三个集合的容斥关系公式:|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C| 详细推理如下: 1、 等式右边改造 = {[(A+B - A∩B)+C - B∩C] - C∩A }+ A∩B∩C 2、维恩图分块标记如右图图:1245构成A,2356构成B,4567构成C 3、等式右边()里指的是下图的1+2+3+4+5+6六部分: 那么A∪B∪C还缺部分7。 4、等式右边[]号里+C(4+5+6+7)后,相当于A∪B∪C多加了4+5+6三部分, 减去B∩C(即5+6两部分)后,还多加了部分4。 5、等式右边{}里减去C∩A (即4+5两部分)后,A∪B∪C又多减了部分5, 则加上A∩B∩C(即5)刚好是A∪B∪C。 例1. 某校六⑴班有学生45人,每人在暑假里都参加体育训练队,其中参加足球队的有25人,参加排球队的有22人,参加游泳队的有24人,足球、排球都参加的有12人,足球、游泳都参加的有9人,排球、游泳都参加的有8人,问:三项都参加的有多少人? 分析:参加足球队的人数25人为A类元素,参加排球队人数22人为B类元素,参加游泳队的人数24人为C类元素,既是A类又是B类的为足球排球都参加的12人,既是B类又C类的为足球游泳都参加的9人,既是C类又是A类的为排球游泳都参加的8人,三项都参加的是A类B类C类的总和设为X。注意:这个题说的每人都参加了体育训练队,所以这个班的总人数即为A类B类和C类的总和。 答案:25+22+24-12-9-8+X=45 ,解得X=3 例2. 某个班的全体学生在进行了短跑、游泳、投掷三个项目的测试后,有4名学生在这三个项目上都没有达到优秀,其余每人至少有一项达到了优秀,达到了优秀的这部分学生情况如下表: 短跑 游泳 投掷 短跑 游泳 短跑 投掷 游泳 投掷 短跑 游泳 投掷 1 7 1 8 1 5 6 6 5 2 求这个班的学生共有多少人? 分析:这个班的学生数,应包括达到优秀和没有达到优秀的。 4+17+18+15-6-6-5+2=39(人) 例3. 在一根长的木棍上有三种刻度线,第一种刻度线将木棍分成10等份,第二种将木棍分成12等份,第三种将木棍分成15等份。如果沿每条刻度线将木棍锯断,木棍总共被锯成多少段? 分析: 很显然,要计算木棍被锯成多少段,只需要计算出木棍上共有多少条不同的刻度线,在此基础上加1就是段数了。 若按将木棍分成10等份的刻度线锯开,木棍有9条刻度线。在此木棍上加上将木棍分成12等份的11条刻度线,显然刻度线有重复的,如5/10和6/12都是1/2。同样再加上将木棍分成15等份的刻度线,也是如此。所以,我们应该按容斥原理的方法来解决此问题。用容斥原理的那一个呢?想一想,被计数的事物有那几类?每一类的元素个数是多少? 解答 解一:[10,12,15]=60,设木棍60厘米 60÷10=6厘米,60÷12=5厘米,60÷15=4(厘米 10等分的为第一种刻度线,共10-1=9(条) 12等分的为第二种刻度线,共12-1=11(条) 15等分的为第三种刻度线,过15-1=14(条) 第一种与第二种刻度线重合的[6,5]=30,60÷30-1=2-1=1(条) 第一种与第三种刻度线重合的[6,4]=12,60÷12-1=5-1=4(条) 第二种与第三种刻度线重合的[5,4]=20,60÷20-1=3-1=2(条) 三种刻度线重合的没有,[6、5、4]=60 因此,共有刻度线9+11+14-1-4-2=27条,木棍总共被锯成27+1=28段。 解二: 10、12、15的最小公倍数是60,假设木棍就是长60, 1、那么,分成10等份的每份6,刻度就是 0,6,12,18,24,30,36,42,48,54,60 2、分成12等分的每份就是5, 0,5,10,15,20,25,30,35,40,45,50,55,60 3、分成15等分的每份就是4, 0,4,8,12,16,20,24,28,32,36,40,44,48,52,56,60 4、把相同刻度的合并,就是有刻度如下: 0,4,5,6,8,10,12,15,16,18,20,24,25,28,30,32,35,36,40,42,44,45,48,50,52,54,55,56,60 例4:小明、小刚、小红、小英四人一起参加一次英语考试,已知考试共有100道题,且小明做对了79题,小刚做对了88题,小红做对了91题,小英作对了89题。 问题: ①小明和小刚都最对的题目至少有几题? ②小明、小刚、小红都最对的题目至少有几题? ③小明、小刚、小红、小英四人最对的题目至少有几题? 解析: ①小明和小刚都最对的题目至少有79+88-100=67人 ②小明、小刚、小红都最对的题目至少有79+88+91-2×100=58人 ③小明、小刚、小红、小英四人最对的题目至少有79+88+91+89-3×100=47人。查看更多