《同步导学案》人教六年级数学（下册）第六单元 第十课时

《同步导学案》人教六年级数学（下册）第六单元 第十课时

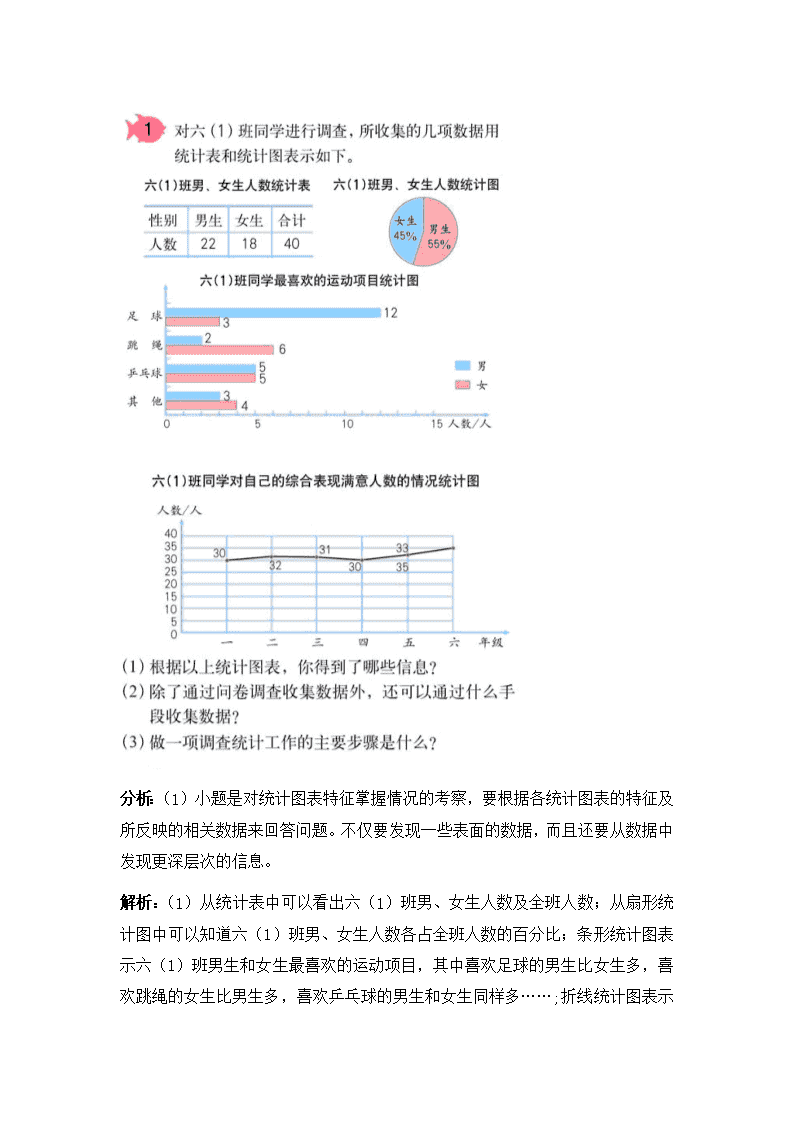
‎3.统计与可能性 ‎1、了解各种统计图表的特征，能够灵活应用各种统计图表。‎ ‎2、掌握平均数、众数和中位数的初步知识，进一步理解平均数、中位数和众数这三种统计量的实际意义。‎ ‎3、重难点：能根据具体情境灵活地选择恰当的统计量来反映数据的不同特点。‎ 知识导入 ‎ 统计在人们的生活中有着广泛的应用。我们在做一些事情之前，要先收集和分析数据，再作出决定。例如，学校了解学生体质健康情况，要收集学生身高、体重等数据，统计就是帮助人们整理和分析数据的知识和方法，大家回忆一下，我们学习过哪些统计知识，你会做一项调查统计并进行数据分析吗？这节课，我们就来复习统计的相关知识。‎ 知识讲解 知识点一 统计表和统计图 分析：（1）小题是对统计图表特征掌握情况的考察，要根据各统计图表的特征及所反映的相关数据来回答问题。不仅要发现一些表面的数据，而且还要从数据中发现更深层次的信息。‎ 解析：（1）从统计表中可以看出六（1）班男、女生人数及全班人数；从扇形统计图中可以知道六（1）班男、女生人数各占全班人数的百分比；条形统计图表示六（1）班男生和女生最喜欢的运动项目，其中喜欢足球的男生比女生多，喜欢跳绳的女生比男生多，喜欢乒乓球的男生和女生同样多……‎ ‎;折线统计图表示六（1）班同学对自己各年级时的综合表现满意人数随着年级的变化情况，其中六年级时，对自己的综合表现最满意的同学最多。（答案不唯一，只要符合统计图、表反映信息即可。）‎ ‎（2）除了问卷调查数据外，还可以通过现场访问调查、查阅文献资料、实验、上网查询等手段来收集数据。‎ ‎（3）做一项调查统计工作的主要步骤：收集数据——整理数据——描述数据——分析数据 点拨：根据调查目的的不同，结合各种统计图、表的作用选择恰当的统计图、表来表示数据。‎ 知识点二 平均数、中位数、众数 分析：（1）题是对平均数、中位数和众数这三个常用统计量求法的考察。平均数等于身高（体重）总和除以总人数；中位数是把这40个数据按大小顺序排列，再用最中间的两个数据之和除以2；众数则是这组数据中出现次数最多的数据。‎ ‎（2）题中，在第一组数据中，通过数每个数据的个数即可以看出中位数和众数都是1.52。以1.52为界，小于1.52的数据个数多于大于1.52的数据个数，所以改组数据的平均数应小于1.52。在第二组数据中，中位数和众数也可以直接通过数据的个数看出，即都是39。以39为界，小于39的数据个数少于大于39的数据个数，所以该组数据的平均数应大于39。‎ ‎（3）中，在这两组数据中，最大数据与最小数据相差不太大，故用平均数可以反映这两组数据的总体水平。‎ 解析：（1）第一组数据 ‎ 平均数：（1.40×1+1.43×3+1.46×5+1.49×10+1.52×12+1.55×6+1.58×3）÷（1+3+5+10+12+6+3）=60.17÷40≈1.50‎ ‎ 中位数：（1.52+1.52）÷2=1.52‎ ‎ 众数：1.52‎ ‎ 第二组数据 ‎ 平均数：（30×2+33×4+36×5+39×12+42×10+45×4+48×3）÷（2+4+5+12+10+4+3）=1584÷40=39.6‎ ‎ 中位数：（39+39）÷2=39‎ ‎ 众数：39‎ 答：第一组数据中，平均数是1.50，中位数是1.52，众数是1.52；第二组数据中，平均数是39.6，中位数是39，众数是39。‎ ‎（2）不用计算，能发现两组数据的平均数、中位数和众数之间的大小关系。在第一组数据中，中位数和众数相等，平均数小于中位数和众数；在第二组数据中，中位数和众数相等，平均数大于中位数和众数。‎ ‎（3）用平均数表示上面两组数据的一般水平比较合适。‎ 点拨：平均数需要通过计算才能得到，而众数和中位数需要观察或排序就能知道。平均数表示的是一组数据的平均值，而众数表示的是一组数据中出现次数最多的那个数；中位数则表示这一组数据中最中间的那个量。虽然三个数据有所不同，但它们都能反映一组数据的一般水平，具有一定的代表性。我们要根据具体的情况，选择不同的统计量来代表一组数据的整体水平。‎ 知识点三 可能性 分析：此题是对判定游戏公平性这一能力的考察，谁的方法中代表三个人的时间出现的可能性相等，则选谁的方法。‎ 解析：第一种方法不合理。在圆形转盘上按三人年龄的大小来分，显然表格所对应的区域要大，指针指向表哥的可能性就大，表哥赢的可能性就大，因此不合理。‎ ‎ 第二种方法公平。在第2个圆形转盘中，代表三方的区域大小相同，这三个人获胜的可能性各是，因此此法公平。‎ 第三种方法公平。设计3个签，在其中1个上面作上记号，同时抽签并打开，那么3个人抽到作记号签的可能性相等，因此此法公平。‎ 点拨：设计抽签方案时，如果不是一次性抽签，并且先抽到的把签打开，那么这种方法也是不公平的。‎ 知识探究 ‎1、 统计表和统计图 ‎（1）统计表的分类 单式统计表：只有一组统计项目的统计表，叫做单式统计表。‎ 复式统计表：有两组或两组以上统计项目的统计表，叫做复式统计表。‎ ‎（2）条形统计图、折线统计图和扇形统计图的特点和作用。‎ 条形统计图 折线统计图 扇形统计图 特点 用一个单位长度表示一定的数量。‎ 用整个圆的面积表示总数，用圆内的扇形面积表示各部分占总数的百分比 用直条的长短表示数量的多少。‎ 用折线的起伏表示数量的增减变化。‎ 作用 从图中能清楚地看出各数量的多少。‎ 从图中能清楚地看出数量增减变化的情况，也能看出数量的多少。‎ 从图中能清楚地看出各部分与总数的百分比，以及部分与部分之间的关系。‎ 例：填空 学校统计四、五、六三个年级同学捐书数量，为了清除地表示各个年级捐书数量与捐书总数之间的关系，应用（ ）统计图；某省统计近期禽流感疫情，既要知道每天患病动物数量的多少，又能反映疫情变化的情况和趋势，最好选用（　　）。‎ 解析：因为条形统计图能清楚地看出各数量的多少，故第一个空应填条形统计图；因为折线统计图不仅能清楚地看出数量增减变化的情况，也能看出数量的多少，故第二个空应填折线统计图。‎ ‎2、 平均数、中位数、众数 平均数、中位数和众数是三个常见的统计量。‎ ‎（1）、平均数：‎ 求平均数的实质就是将几个数量，在总量（和）不变的情况下，通过移多补少，使它们变为相等。求平均数的基本数量关系式是：总数量÷总份数=平均数。解题的关键是根据已知条件确定总数量及与它相对应的总份数。‎ ‎（2）、中位数：把调查得到的一组数据，按照大小顺序排列起来，其中处于正中间的那一个数据叫做这组数据的中位数。如果数据是偶数个，则取正中间的两个，计算出这两个数据的平均数作为该组数据的中位数。‎ ‎（3）、众数：在一组数据中，出现次数最多的那个数就叫做这组数据的众数。如果一组数据出现次数最多的数据有多个，那么这组数据的众数就有多个。‎ 例：填空 ‎ 5,8,8,9,14这组数据的平均数是（ ），中位数是（ ），众数是（ ）。‎ 解析：（5+8+8+9+14）÷5=8.8 所以平均数是8.8；中位数是5个数据中最中间的那个，所以是8；在这5个数据中，只有8出现2次，其它数据都只出现1次，所以众数是8。‎ ‎3、 可能性 ‎（1）、确定事件和不确定事件 生活中，有些事件的发生是不确定的，一般用“可能发生”来描述；有些事件的发生是确定的，一般用“一定发生”或“不可能发生”来描述。‎ ‎（2）、体验事件发生的等可能性及游戏规则的公平性，能设计公平的、符合指定要求的游戏规则或方案。会求一些简单事件发生的可能性。‎ 例：同时扔两枚硬币，如果一正一反则李丽胜，两个同时为正面或同时为反面则王军胜，这个游戏公平吗？说明理由。如果扔100次，两个都是正面大约会出现多少次？‎ 解析：公平，同时扔两枚硬币，会出现四种不同情况，分别是：正正、正反、反正、反反。所以李丽和王军获胜的可能性各为。如果扔100次，两个都是正面大约会出现100×=25次。‎ 同步练习 一、填一填。‎ ‎1、某公司统计去年1~12月的电动车的生产量，绘制（ ）统计图，能比较清楚反映出各月电动车的生产量；如果要反映各月生产量的增减变化情况，可以绘制（ ）统计图。‎ ‎2、一组数据16， b， 12， 14的平均数是14，这组数据的中位数是（ ）。‎ ‎3、盒子里装有大小、形状相同的红球、黄球共12个，如果任意摸一个球，摸到红球的可能性大，则红球至少有（ ）个。‎ ‎4、某班民主选举班委，有8名同学参加竞选（以编号代替姓名），全班48名同学参加了投票选举。得票情况吐下：‎ 编号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 票数 ‎39‎ ‎23‎ ‎43‎ ‎18‎ ‎41‎ ‎46‎ ‎18‎ ‎42‎ ‎（1）得票最多的是（ ）号同学。‎ ‎（2）得票超过半数的同学能当选为本班班委。那么，这次民主选举（ ）同学竞选成功，光荣地当选为本班班委，当选率为（ ）%。‎ 二、我是小法官。（对的打“√”，错的打“×”）‎ ‎1、一个池塘的平均深度是120厘米，小明的身高是135厘米，小明在这个池塘中游泳没有危险。（　　　）‎ ‎２、家里又２０瓶饮料，其中有２瓶已经过期，妈妈随便拿了１瓶。拿出来的一定是不过期的。（　　　　）。‎ ‎３、北京地区的天气预报播报：今天阴有小雨转多云，降水概率９０％。小军说：“今天要带伞，下雨的可能性很大。”　（　　　）‎ ‎４、在一组数据中可能没有众数，但一定有中位数。（ ）‎ ‎5、在国际象棋小组赛中，甲棋手在50%的比赛中都战胜了乙棋手，那么乙棋手战胜甲棋手的可能性小于。‎ 三、对号入座。（请将正确答案的序号填在括号里）‎ ‎1、下列的信息资料中，不适合用条形统计图表示的是（ ）。‎ A学校各年级的人数 B 六年级各班做好事的件数 C 六月份气温变化情况 ‎ ‎2、六（1）班有40人，六（2）班有42人，要比较期末考试时哪个班的成绩高一些，应该选取（ ）。 ‎ ‎ A 平均数；B 中位数 C 众数 ‎3、“太阳从东方升起，从西方落下”这件事是（ ）会发生的。 ‎ A一定 B可能 C不可能 ‎4、用1,2,3三个数字组成一个三位数，则组成偶数的可能是（　　）。‎ A、 B、 C、 四、综合应用。‎ ‎1、信息统计。‎ 我国南方某市2011年月平均气温统计图 根据上面统计图提供的数据填空。‎ ‎(1)这座城市2011年的月平均气温，从( )月开始逐渐上升，( ‎ ‎ )月的月平均气温最高。‎ ‎(2) 这座城市2011年的月平均气温，从( )月开始逐渐下降，( )月的月平均气温最低。‎ ‎(3)( )月与( )月之间的平均气温上升得最快，( )月与( )月之间的平均气温下降得最快。‎ ‎2、六年级（2）班的一次数学测验，全班都达到及格线以上，具体统计如下图：‎ ‎(1)请在纵轴括号内标出每个刻度表示的数。‎ ‎(2)已知在及格段的女生人数是5人，请在图上用表示出来，将条形统计图补充完整。‎ ‎(3)求这次测验中，全班的优秀率是多少？‎ 参考答案 一、1、条形 折线 2、14 3、7 4、（1）6 （2）5 62.5 ‎ 二、1、× 2、× 3、√ 4、× 5、×‎ 三、1、Ｃ　２、A　３、A　４、A 四、1、（1）一 八 （2）八 一 （3）四 五 十 十一 ‎ ‎2、（1）从下到上依次是：2 4 6 8‎ ‎ （2）略 ‎ ‎（3）（5+4）÷（5+4+6+10+6+5）=25% 答：这次测验中，全班的优秀率是25%。‎