- 2022-02-10 发布 |
- 37.5 KB |
- 29页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
六年级数学下册期末复习课件- 比例 -人教新课标(共29张PPT)
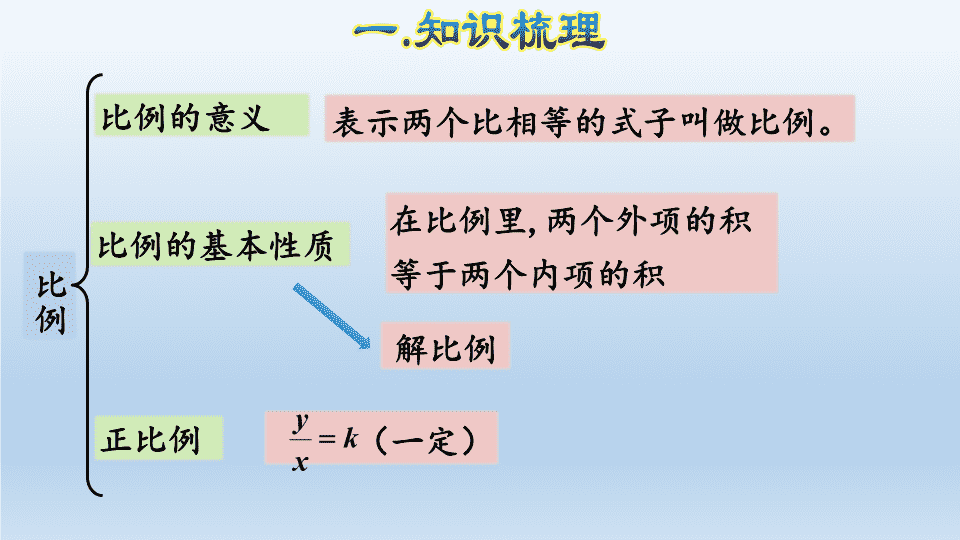
期末复习课件 比例 在一个比例里,两个内项互为倒数,其中一个外项是10以内既是奇数又是合数的数,则另一个外项是( )。 比例 比例的意义 解比例 比例的基本性质 正比例 表示两个比相等的式子叫做比例。 在比例里 , 两个外项的积等于两个内项的积 (一定) 比例 比例尺 图上距离 ∶ 实际距离=比例尺 图形的放大与缩小 形状相同,大小不同 反比例 x y = k (一定) 1 . 比例的意义 判断两个比能否组成比例的方法: 根据比例的意义,看两个比的比值是否相等,相等就能组成比例。 对应训练 1 判断下列各组中的四个数能否组成比例,如果能,把组成的比例写下来。 (1) 4 , 20 , 5 和 1 ( ) ___________________________________________ (2) 2 , 0.6 , 5 和 2.5 ( ) ___________________________________________ 能 20:4 = 5:1( 所写比例不唯一 ) 不能 2 . 比例的基本性质 什么叫做比例的项?比例的外项?比例的内项?举例。 用字母表示比例的基本性质: a ∶ b = c ∶ d ( b 、 d ≠0 ) = 或 ad = bc 对应训练 2 把 a × b = c × d ( a , b , c , d 均不为 0) 改写成比例式,你可以写出几个? 8 个,分别是 a : c = d : b b:c = d:a c:a = b:d d:a = b:c a:d = c:b b:d = c:a c:b = a:d d:b = a:c 对应训练 2 解比例: 3 x = 12 2.4 12 x = 2.4 × 3 12 x = 7.2 x = 0.6 解: 3 . 正比例 判断两个量是否成正比例关系的基本步骤: 1. 首先判断两个量是否是相关联的量。 2. 然后再看两个量的商是否为定值。 x y = k (一定) 正比例图象的特点: 正比例关系的图象是一条直线。从图象中可以直观地看到相对应两种量的变化情况。不用计算,由一个量的值可以直接找到相对应的另一个量的值。 对应训练 3 下表中关于正方体的一些数量,哪两种量成正比例关系?说明理由。 棱长 /cm 1 2 3 4 底面积 /cm 2 1 4 9 16 表面积 /cm 2 6 24 54 96 体积 /cm 3 1 8 27 64 质量 /g 7.8 62.4 210.6 499.2 正方体的表面积和底面积成正比例关系。 因为:表面积 ÷ 底面积= 6 。 正方体的质量与体积成正比例关系。 因为:质量 ÷ 体积=每立方厘米的质量 ( 一定 ) 。 4. 反比例 判断两个量是否成反比例关系的基本步骤: 1. 首先判断两个量是否是相关联的量。 2. 然后再看两个量的积是否为定值。 xy = k (一定) 对应训练 4 甲、乙、丙、丁每人买一本 《 童话故事 》 ,他们每天看的页数与看完这本书需要的天数的情况如下: (1) 把下表补充完整。 甲 乙 丙 丁 每天看的页数 / 页 10 15 25 30 需要的天数 / 天 15 10 6 5 (2) 每天看的页数和需要的天数成什么关系?为什么? (3) 已经看了 4 天,剩下的页数和已看的页数成反比例关系吗? 每天看的页数和需要的天数成反比例关系。 因为每天看的页数 × 需要的天数=总页数 ( 一定 ) 。 每天看的页数和需要的天数成反比例关系。 因为每天看的页数 × 需要的天数=总页数 ( 一定 ) 。 5 . 比例尺 图上距离 ∶ 实际距离=比例尺 实际距离 图上距离 =比例尺 或 根据比例尺的表现形式分为:数值比例尺和线段比例尺 根据比例尺的作用不同分为:放大比例尺和缩小比例尺 1∶100000000 2∶1 1∶100000000 对应训练 5 北京到天津的实际距离是 120 km ,在地图上量得的距离是 6 cm 。下面是这幅地图的比例尺,你能把它补充完整吗? 40 60 80 20 图形的放大与缩小是生活中常见的现象,把一 个图形放大或缩小后所得的图形与原来的图形相比, 形状相同,大小不同 。 6. 图形的放大与缩小 对应训练 6 判断: 一个正方形按4:1放大后,面积扩大为原来的16倍。 ( ) 1 .甲数的 等于乙数的 (甲数、乙数均不为0),则甲数:乙数=( ):( )。 2 .如果 x =6 y ( y ≠0),那么 x 和 y 成( )比例关系。 3 .三角形的面积一定,底和高成( )比例关系。 10 9 正 反 一、填空。 4 .线段比例尺,表示图上( )相当于( )。按这样的比例尺,图上4 cm表示实际距离( )。 1 cm 实际距离 200 km 50 km 二、判断。 1.如果4 m =5 n ,那么 m : n =4:5。 ( ) 2.比例尺实际上是一个比。 ( ) 3.同一时间、同一地点,物体的影长与物体的高度成正比例关系。 ( ) 三、选择。 下面每组的两个量中,成反比例关系的是( )。 A.一袋大米,已经吃了的和没吃的 B.乐乐的年龄和体重 C.一个圆锥的体积是48 dm 3 ,它的底面积和高 D.房间的面积一定,每块正方形瓷砖的边长和所 需的块数 C 四、解决问题。 1. 在一幅比例尺是 1:600000 的地图上, 量得甲、乙两地 的距离是 40 cm 。一辆汽车从甲地到乙地,要求 4 小时 到达,平均每小时行多少千米? 40÷ = 40×600000 = 24000000(cm) = 240(km) 240÷4 = 60(km) 答:平均每小时行 60 千米。 2 .甲、乙两地间的距离是490 km,一辆汽车从甲 地出发去乙地,5小时行驶了350 km。照这样计算,行完全程还要几小时?(用比例解) 解:设行完全程还要 x 小时。 = x =2 答: 行完全程还要 2 小时 。 3.一个长方形的长是12 cm,宽是5 cm。如果按3:1 放大,得到的长方形的面积和周长分别是多少? 12×3=36(cm) 5×3=15(cm) S =36×15=540(cm 2 ) C =(36+15)×2=102(cm) 谢 谢查看更多