小学数学精讲教案4_3_2 三角形等高模型与鸟头模型（二） 学生版

小学数学精讲教案4_3_2 三角形等高模型与鸟头模型（二） 学生版

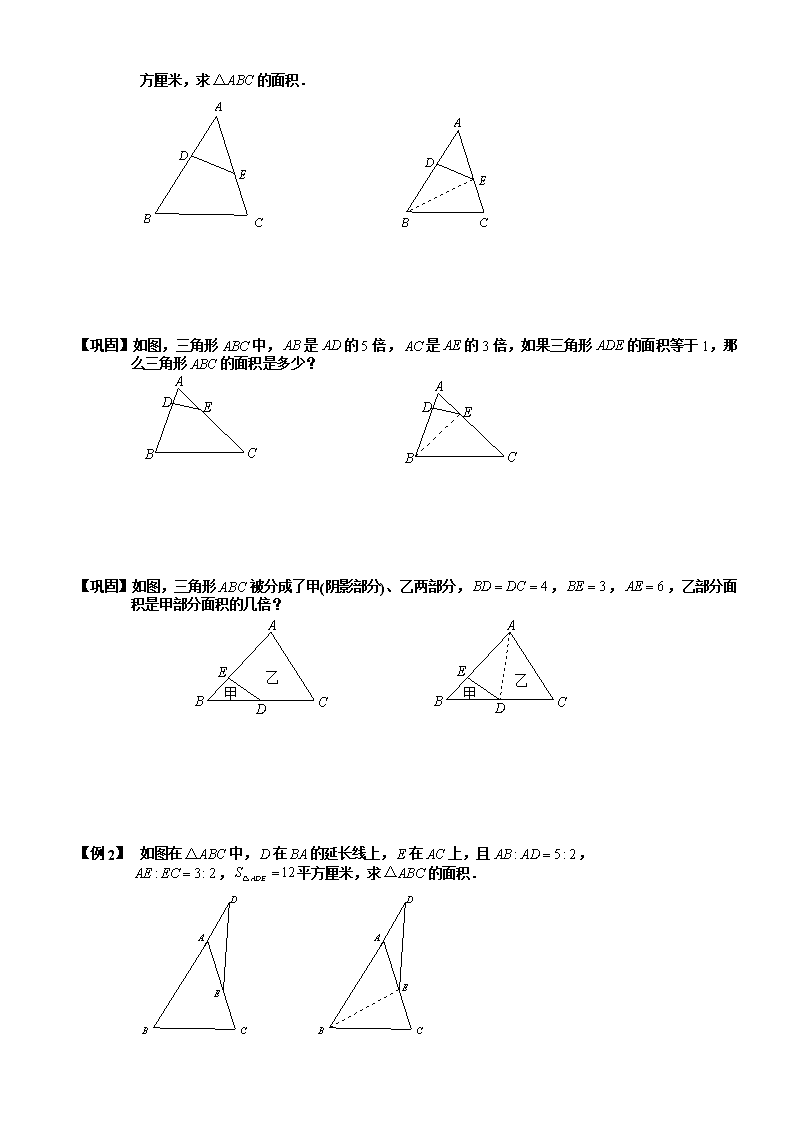
‎4-3-2.三角形等高模型与鸟头模型 例题精讲 板块一 三角形等高模型 我们已经知道三角形面积的计算公式：三角形面积底高 从这个公式我们可以发现：三角形面积的大小，取决于三角形底和高的乘积．‎ 如果三角形的底不变，高越大(小)，三角形面积也就越大(小)；‎ 如果三角形的高不变，底越大(小)，三角形面积也就越大(小)；‎ 这说明当三角形的面积变化时，它的底和高之中至少有一个要发生变化．但是，当三角形的底和高同时发生变化时，三角形的面积不一定变化．比如当高变为原来的3倍，底变为原来的，则三角形面积与原来的一样．这就是说：一个三角形的面积变化与否取决于它的高和底的乘积，而不仅仅取决于高或底的变化．同时也告诉我们：一个三角形在面积不改变的情况下，可以有无数多个不同的形状．‎ 在实际问题的研究中，我们还会常常用到以下结论：‎ ‎①等底等高的两个三角形面积相等；‎ ‎②两个三角形高相等，面积比等于它们的底之比；‎ 两个三角形底相等，面积比等于它们的高之比；‎ 如左图 ‎ ‎ ‎③夹在一组平行线之间的等积变形，如右上图；‎ 反之，如果，则可知直线平行于．‎ ‎④等底等高的两个平行四边形面积相等(长方形和正方形可以看作特殊的平行四边形)；‎ ‎⑤三角形面积等于与它等底等高的平行四边形面积的一半；‎ ‎⑥两个平行四边形高相等，面积比等于它们的底之比；两个平行四边形底相等，面积比等于它们的高之比．‎ 板块二 鸟头模型 两个三角形中有一个角相等或互补，这两个三角形叫做共角三角形．‎ 共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比．‎ 如图在中，分别是上的点如图 ⑴(或在的延长线上，在上)，‎ 则 ‎ ‎ 图⑴ 图⑵‎ 【例 1】 如图在中，分别是上的点，且，，平方厘米，求 的面积．‎ ‎ ‎ ‎【巩固】如图，三角形中，是的5倍，是的3倍，如果三角形的面积等于1，那么三角形的面积是多少？‎ ‎ ‎ ‎【巩固】如图，三角形ABC被分成了甲(阴影部分)、乙两部分，，，，乙部分面积是甲部分面积的几倍？‎ ‎ ‎ 【例 1】 如图在中，在的延长线上，在上，且，‎ ‎，平方厘米，求的面积．‎ ‎ ‎ 【例 1】 如图所示，在平行四边形ABCD中，E为AB的中点，，三角形AFE(图中阴影部分)的面积为8平方厘米．平行四边形的面积是多少平方厘米？‎ 【例 2】 已知的面积为平方厘米，，求的面积．‎ 【例 3】 如图16-4，已知．AE=AC，CD=BC，BF=AB，那么等于多少?‎ ‎ ‎ 【例 4】 如图，三角形的面积为3平方厘米，其中，，三角形的面积是多少？‎ 【例 5】 如图所示，正方形边长为‎6厘米，，．三角形的面积为_______平方厘米．‎ 【例 1】 如图，已知三角形面积为，延长至，使；延长至，使；延长至，使，求三角形的面积．‎ ‎ ‎ 【例 2】 如图，把四边形ABCD的各边都延长2倍，得到一个新四边形EFGH如果ABCD的面积是5平方厘米，则EFGH的面积是多少平方厘米?‎ 【例 3】 如图，平行四边形，，，，，平行四边形的面积是， 求平行四边形与四边形的面积比．‎ ‎ ‎ 【例 1】 如图，四边形的面积是平方米，，，，，求四边形的面积．‎ ‎ ‎ 【例 2】 如图，将四边形的四条边、、、分别延长两倍至点、、、，若四边形的面积为5，则四边形的面积是 ．‎ ‎ ‎ 【例 3】 如图，在中，延长至，使，延长至，使，是的中点，若的面积是，则的面积是多少？‎ 【例 4】 如图，，，，，．求．‎ 【例 5】 如图所示，正方形边长为厘米，是的中点，是的中点，是的中点，三角形 的面积是多少平方厘米？‎ ‎ ‎ 【例 1】 四个面积为的正六边形如图摆放，求阴影三角形的面积．‎ ‎ ‎ ‎【巩固】已知图中每个正六边形的面积都是1，则图中虚线围成的五边形的面积是 ．‎ ‎ ‎ 【例 2】 仅用下图这把刻度尺，最少测量 次，就能得出三角形ABC和三角形BCD的面积比。‎