人教版五年级上册数学第五单元简易方程 教学课件（2）

人教版五年级上册数学第五单元简易方程 教学课件（2）

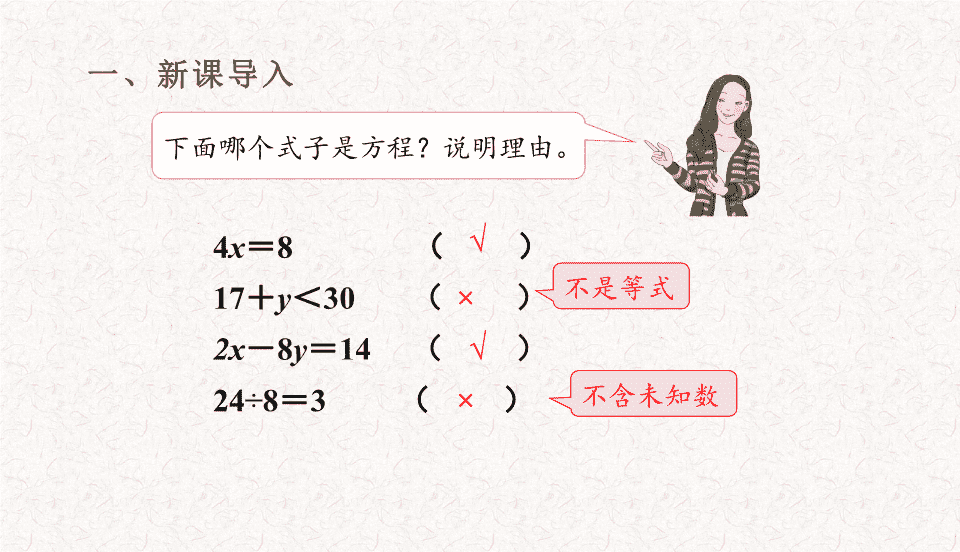
简易方程5 人教版·五年级上册 第9课时 解方程（1） 一、新课导入 4x＝8 （ ）√ 2x－8y＝14 （ ） 17＋y＜30 （ ） × 24÷8＝3 （ ） √ × 下面哪个式子是方程？说明理由。 不是等式 不含未知数 一、新课导入 谁能说说等式的性质是什么？ 等式的性质1： 等式两边加上或减去同一个数，左右两边仍然相等。 等式的性质2： 等式两边乘同一个数，或除以同一个不为0的数，左右两边仍然相等。 二、例题讲解 你能根据图意列出方程吗？你是怎么想的？ x＋3＝9 长方体盒子代表未知的x个球，每个小正方体代表 一个球。则天平左边是x +3个球，右边是9个球，天 平平衡，也就是列式：x +3=9。 二、例题讲解 x的值是多少？你是怎么想的？ 二、例题讲解 方法一： x＋3＝9 由9－3=6， 想6+3=9， 所以x=6。 二、例题讲解 方法二 x＋3＝9 可以用等式的性质来求。 等式两边减去同 一个数，左右两 边仍然相等。 x＋3－3＝9－3 为什么要减3？ x＝6 二、例题讲解 那么这个演算过程应如何书写呢？ 今后我们就可以用等式的性质 来求解方程中未知数的值。 x＋3 = 9 解：x ＋3－3 = 9－3 x = 6 从方程的第二行起写一 个“解：”，利用等式 的性质两边同时减去一 个数，为了美观，要注 意每步等号要对齐。 二、例题讲解 x＝6 x＋3＝9 解：x＋3－3＝9－3 求方程的解的过 程叫做解方程。 使方程左右两边相等 的未知数的值，叫做 方程的解。 二、例题讲解 x＝6是不是正确的答案呢？请你检验一下。 x＋3＝9 解： x＋3－3＝9－3 ＝6＋3 ＝9 ＝方程右边 所以，x＝6是方程的解。 方程左边＝x＋3 x＝6 二、例题讲解 解方程 3x＝18。 说一说你的想法。 二、例题讲解 3x = 18 解：3x÷( ) = 18÷( ) x = ( ) 3 3 6 我是借助天平来解答的。 等式两边同时除以一个不为0的 数，左右两边仍然相等。 依据是什么？ 二、例题讲解 规范解答 解方程 3x＝18。 3x＝18 解：3x÷3＝18÷3 x＝6 二、例题讲解 解方程 20－x＝9 请大家尝试解答。说一说你的想法。 你遇到了什么困难？ 二、例题讲解 20－x＝9 解：20－x－20＝9－20 x＝9－20 ？ 上面的解法对吗？说一说你们 是如何解决这个问题的？ 二、例题讲解 规范解答 20－x＝9 x＝11 解：20－x＋x＝9＋x 20＝9＋x 9＋x＝20 9＋x－9＝20－9 等式两边加上相 同的式子，左右 两边仍然相等。 ＋x ＋x 二、例题讲解 x=11是不是正确的答案呢？ 检验一下。 检验： 方程左边＝20－x ＝20－11 ＝9 ＝方程右边 所以，x＝11是方程的解。 三、新知应用 1. 解下列方程。 解： x+3.2-3.2＝4.6-3.2 x＝1.4 x+3.2＝4.6 15－x＝2 解:15－x＋x＝2+x 15=2+x 2+x=15 2+x-2=15-2 x=13 解：1.6x÷1.6＝6.4÷1.6 x＝4 1.6x＝6.4 三、新知应用 2. x＝2是方程5x＝15的解吗？x＝3呢？ 方程左边＝5x ＝5×2 ＝10 ≠方程右边 所以，x＝2不是方程的解。 三、新知应用 2. x＝2是方程5x＝15的解吗？x＝3呢？ 方程左边＝5x ＝5×3 ＝15 ＝方程右边 所以，x＝3是方程的解。 三、新知应用 8.4元 x元 x元 x元 3.列方程并解答。 解：3x÷3＝8.4÷3 x＝2.8 3x＝8.4 4元 x元 解：x+1.2-1.2＝4-1.2 x＝2.8 x+1.2＝4 1.2元 四、课堂小结 通过这节课，你有什么新的收获？ 2.使方程左右两边相等的未知数的值，叫做方程的解。 3.求方程的解的过程叫做解方程。 1．解方程时是根据等式的性质来解。。 五、课后作业 完成课本第70页练习十五第1、2题。 简易方程5 人教版·五年级上册 第10课时 解方程（2） 一、新课导入 说说上节课我们学了什么？ 2.使方程左右两边相等的未知数的值，叫做方程的解。 3.求方程的解的过程叫做解方程。 1．解方程时是根据等式的性质来解。。 一、新课导入 3.5x=10.5 解：3.5x÷3.5=10.5÷3.5 x=3 43－x=24 解：43－x＋x=24＋x 43=24＋x 24＋x=43 x=19 解下列方程。 二、例题讲解 看图列方程，并求出方程的解。 你知道了什么信息？ 二、例题讲解 3x＋4＝40 + 铅笔总数量 盒子外的铅笔数量盒子里的铅笔数量 你能根据题意列出 方程吗？ 二、例题讲解 3x＋4＝40 怎么解这个方程呢？ 解：3x＋4－4＝40－4 3x＝36 x＝12 3x÷3＝36÷3 把3x看成一个整体。 二、例题讲解 2(x－16)＝8 如何解这个方程？ x－16＝4 解：2(x－16)÷2＝8÷2 x＝20 x－16＋16＝4＋16 把什么看成 一个整体？ 二、例题讲解 2x＝40 解： 2 x－32＝8 x＝20 2x－32＋32＝8＋32 2x÷2＝40÷2 运用了什么定律？ 乘法分配律 2(x－16)＝8 还可以这样解。 二、例题讲解 检验： 方程左边＝2（x－16） ＝2×（20－16） ＝2×4 ＝方程右边 所以，x＝20是方程的解。 检验一下，做得对吗？ 三、新知应用 1. 看图列方程，并求出方程的解。 7.5元 x元/本 1.5元 5x+1.5=7.5 解：5x+1.5-1.5=7.5-1.5 5x=6 5x÷5=6÷5 x=1.2 三、新知应用 6x-35=13 3x-12×6=6 解： 6x-35+35=13+35 6x=48 6x÷6=48÷6 x=8 解： 3x-72=6 3x-72+72=6+72 3x=78 3x÷3=78÷3 2.解下面的方程。 x=26 三、新知应用 （5x-12）×8=24 解：（5x-12）×8÷8=24÷8 5x-12=3 5x=15 x=3 （100-3x）÷2=8 解：（100-3x）÷2×2=8×2 100-3x=16 100-3x+3x=16+3x 100=16+3x 3x=84 x=28 四、课堂小结 通过这节课，你有什么新的收获？ 解 方 程 形如ax±b=c的方程 形如a(x±b)=c的方程 把ax看成一个整体 把(x±b)看成一个整体 五、课后作业 完成课本第71页练习十五第8、9题。 简易方程5 人教版·五年级上册 第11课时 练习十五 x+0.3=1.8 解：x+0.3-0.3=1.8-0.3 x=1.5 解下列方程。 6.3÷x=7 解：6.3÷x×x=7x 7x=6.3 7x÷7=6.3÷7 x=0.9 一、复习巩固 解方程知识点1 5x=1.5 解：5x÷5=1.5÷5 x=0.3 43-x=38 解：43-x+x=38+x 43=38+x 38+x=43 38+x-38=43-38 x=5 基础练习 P70 4.用方程表示下面的等量关系，并求出方程的解。 （1）x 加上 35 等于 91 。 （2）x 的 3 倍等于 57 。 x+35=91 3x=57 解：x+35-35=91-35 x=56 解：3x÷3=57÷3 x=19 基础练习 二、课堂练习 P70 4.用方程表示下面的等量关系，并求出方程的解。 （3）x 减 3 的差是 6 。 （4）x 除以 8 等于 1.3 。 x-3=6 解：x-3+3=6+3 x=9 x÷8=1.3 解：x÷8×8=1.3×8 x=10.4 二、课堂练习 P71 8.看图列方程，并求出方程的解。 x+50=100+100 解：x+50-50=200-50 x=150 （1) 二、课堂练习 P71 8.看图列方程，并求出方程的解。 （2) 30+30+x+x=158 解：60+2x=158 60+2x-60=158-60 2x=98 2x÷2=98÷2 x=49 二、课堂练习 P71 10.用线段把下面每个方程和它的解连起来。 二、课堂练习 P72 11.看图列方程并求解。 2(x+5)=36 解：2(x+5)÷2=36÷2 x+5=18 x+5-5=18-5 x=13 周长36m xm 5m 二、课堂练习 P72 解：4x=80 4x÷4=80÷4 x=20 11.看图列方程并求解。 x+3x=80 二、课堂练习 14*.在□里填上适当的数，使每个方程的解都是x=5。 □+x=13 x-□= 2.3 □×x= 7 x÷□=50 8 2.7 1.4 0.1 P72 方 程 的 解 法 方程的解 解 方 程 使方程左右两边相等的未知数的值， 叫做方程的解。 形如ax=b的方程 解：ax÷a=b÷a x=b÷a 形如a－x=b的方程 解：a－x+x=b+x b+x=a x=a-b 形如ax±b=c的方程把ax看成一个整体 形如a(x±b)=c的方程把(x±b)看成一个整体 知识总结 三、课后作业 完成练习十五第70-72页第3、5、6、13题。 简易方程5 人教版·五年级上册 第12课时 实际问题与方程（1） 一、新课导入 1．解下列方程。 3x+6=18 2x-7.5=8.5 16+8x =40 4x-3×9=29 解：3x+6-6=18-6 3x=12 3x÷3=12÷3 x=4 解：2x-7.5+7.5=8.5+7.5 2x=16 2x÷2=16÷2 x=8 解：16+8x-16=40-16 8x=24 8x÷8=24÷8 x=3 解：4x-27=29 4x-27+27=29+27 4x=56 4x÷4=56÷4 x=14 一、新课导入 2．分析数量关系。 (1)我们班男生比女生多8人。 (2)实际用煤比计划节约5吨。 (3)实际水位超过警戒水位0.64 m。 男生人数-8人=女生人数 实际用煤+5吨=计划用煤 实际水位=警戒水位+0.64米 二、例题讲解 学校原跳远纪录是多少米？ 1.请大家认真观察情境图，然后说说从图中获得了哪 些信息。 小明的成绩为4.21m，超过了学校的原纪录0.06m。 二、例题讲解 原纪录 小明 ?m 0.06m 4.21m 原纪录+超出部分=小明的成绩 小明的成绩-超出部分=原纪录 小明的成绩-原纪录=超出部分 你能画图找出等量关系吗？ 二、例题讲解 说一说你的解题方法。 方法一：列算式 小明的成绩-超出部分=原纪录 4.21－0.06=4.15(米) 二、例题讲解 原纪录+超出部分=小明的成绩 由于原纪录是未知数，可以设 它为xm，再列方程解答。 方法二：列方程解答 x+0.06=4.21 二、例题讲解 规范解答 解：设学校原跳远纪录是xm。 x+0.06=4.21 x+0.06-0.06=4.21-0.06 x=4.15 答：学校原跳远纪录是4.15m。 二、例题讲解 还可以怎么列方程？ 解：设学校原跳远纪录是x米。 4.21－x=0.06 4.21－x＋x=0.06＋x 4.21=0.06＋x 0.06＋x=4.21 0.06＋x－0.06=4.21－0.06 x=4.15 答：学校原跳远纪录是4.15米。 小明的成绩-原纪录=超出部分 二、例题讲解 同一个问题，我们用了哪几种不同的 方法解决？ 算术的方法 和列方程解 答的方法。 用方程的思路解决问题时，你认为关 键是什么？ 找出等量关系。 二、例题讲解 列方程解决实际问题的步骤： (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系，列方程； (3)解方程并检验作答。 三、新知应用 小明去年身高多少？ 1.列方程解决下面问题。 解：设小明去年身高x米。 0.08＋x=1.53 0.08＋x－0.08=1.53－0.08 x=1.45 答：小明去年身高1.45米。 8cm＝0.08m （1) 三、新知应用 解:设一个滴水的水龙头每 分钟浪费x千克水。 x=0.06 答:一个滴水的水龙头每分 钟浪费0.06千克水。 半小时＝30分 30x=1.8 30x÷30=1.8÷30 （2) 三、新知应用 解:设黄河长x千米。 x=5464 答:黄河长5464千米。 835+x=6299 835+x-835=6299-835 四、课堂小结 通过这节课，你有什么新的收获？ 列方程解决实际问题的步骤： (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系， 列方程； (3)解方程并检验作答。 关 键 五、课后作业 完成课本第75页练习十六第3、4题。 简易方程5 人教版·五年级上册 第13课时 实际问题与方程（2） 一、新课导入 列方程解决实际问题有哪些步骤？ (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系， 列方程； (3)解方程并检验作答。 关 键 一、新课导入 每平方米阔叶林每天制造75g 氧气，是每平方米草地每天制 造氧气的5倍。每平方米草地 能制造多少克氧气？ 解：设每平方米草地能制造x克氧气。 5x÷5 =75÷5 x =15 答：每平方米草地能制造15克氧气。 5x =75 1.观察上图，并说说从图中你知道了哪些信息？ 2.要解决什么问题？ 足球上黑色的皮都是五边形的，白色的皮都是六边形的。 共有多少块黑色皮？ 白色皮共有20块，比黑色皮的2倍少4块。 二、例题讲解 你能画图找出等量关系吗？ 4块20块 黑色皮 白色皮 2x块 x块 黑色皮块数×2－白色皮块数＝4 黑色皮块数×2＝白色皮块数＋4 二、例题讲解 解：设共有x块黑色皮。 2x－4＝20 先找出问题中的等量关系。 黑色皮的块数×2-4=白色皮的块数 怎样列方程呢？ 二、例题讲解 2x－4＋4=20＋4 x=12 2x÷2=24÷2 2x=24 2x－4=20 怎样解方程呢？ 先把 2x看成 一个整体。 二、例题讲解 解：设共有x块黑色皮。 二、例题讲解 方程左边=2x－4 =2×12－4 =24－4 =20 =方程右边 所以，x=12是方程的解。 怎样知道结果对不对呢？ 可以进行检验。 二、例题讲解 解：设共有x块黑色皮。 2x=20＋4 x=12 2x÷2=24÷2 2x=24 还可以怎样列方程呢？ 黑色皮块数×2＝白色皮块数＋4 答：共有12块黑色皮。 二、例题讲解 列方程解决实际问题有哪些步骤？ (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系，列方程； (3)解方程并检验作答。 三、新知应用 1．根据方程列出等量关系式。 粮店运来72吨大米，比运来的面粉的3倍多12吨。 运来面粉多少吨？ 列方程：3x+12=72 等量关系式：( 面粉的质量×3+12=大米的质量 ) 列方程：72-3x =12 等量关系式：( 大米的质量-面粉的质量×3=12 ) 三、新知应用 5.共有1428个网球，每5个装一筒， 装完后还剩3个。一共装了多少筒？ 解：设一共装了x筒。 5x＋3=1428 5x＋3－3=1428－3 5x=1425 5x÷5=1425÷5 x=285 答：一共装了285筒。 每筒的个数×筒数＋3＝网球总数 P75 三、新知应用 6.故宫的面积是72万平方千米，比天 安门广场面积的2倍少16万平方千米。 天安门广场的面积是多少万平方千米？ 解：设天安门广场的面积是x万平方千米。 2x-16=72 x-16+16=72+16 2x=88 2x÷2=88÷2 x=44 答：天安门广场的面积是44万平方千米。 天安门的面积×2-16＝故宫的面积 P75 四、课堂小结 解形如ax±b=c（a≠0,b≠0)的方程,先把ax看作一个整体,求 出ax等于多少,再求x等于多少。 通过这节课，你有什么新的收获？ 四、课堂小结 通过这节课，你有什么新的收获？ 列方程解决实际问题的步骤： (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系， 列方程； (3)解方程并检验作答。 关 键 五、课后作业 完成课本第76页练习十六第7题。 简易方程5 人教版·五年级上册 第14课时 练习十六 7.宁夏的同心县是一个“干渴”的地 区，年平均蒸发量是 2325 mm，比年 平均降水量的8倍还多109 mm。同心县 的年平均降水量是多少毫米？ P76 年平均降水量×8+109=年平均蒸发量 解：设同心县的年平均降水量是x毫米。 8x+109=2325 8x+109-109=2325-109 8x=2216 x=277 答：同心县的年平均降水量是277毫米。 一、复习巩固 实际问题与方程知识点1 P76 8.猎豹是世界上跑得最快的动物，速度能达到每小时110km， 比大象的2倍还多30km。大象最快能达到每小时多少千米？ 大象的速度×2+30=猎豹的速度 解：设大象最快能达到每小时x千米。 2x+30=110 2x+30-30=110-30 2x=80 x=40 答：大象最快能达到每小时40千米。 基础练习 9.世界上最大的洲是亚洲，面积 是4400万平方千米。最小的洲是 大洋洲，亚洲的面积比大洋洲面积 的4倍还多812万平方千米。大洋 洲的面积是多少万平方千米？ 4x +812=4400 4x +812-812=4400-812 4x=3588 4x÷4=3588÷4 x=897 答：大洋洲的面积是897万平方千米。 P76 大洋洲面积×4 +812=亚洲的面积 解：设大洋洲的面积是x万平方千米。 二、课堂练习 P76 10. 这个小朋友的体温相当于多少摄氏度？ 1.8x +32=98.6 1.8x +32-32=98.6-32 1.8x=66.6 1.8x÷1.8=66.6÷1.8 x=37答：这个小朋友的体温相当于37摄氏度。 解：设这个小朋友的体温相当于x摄氏度。 二、课堂练习 P76 8.当a等于多少时，下面式子的结果是0？当a等于多少时，下 面式子的结果是1？ （36-4a）÷8 （36-4a）÷8=0 解：（36-4a）÷8×8=0×8 36-4a=0 36-4a+4a=0+4a 4a=36 a=9 （36-4a）÷8=1 解：（36-4a）÷8×8=1×8 36-4a=8 36-4a+4a=8+4a 4a=28 a=7 答：当a等于9时，下面式子的结果是0。当a等于7时，下面式子的 结果是1。 二、课堂练习 列方程解决实际问题有哪些步骤？ (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系， 列方程； (3)解方程并检验作答。 关 键 知识总结 三、课后作业 解下列方程。 4x+13=365 3x+2×7=50 4x+2.1=8.5 48.34-3.2x=4.5 简易方程5 人教版·五年级上册 第15课时 实际问题与方程（3） 一、新课导入 (1)舞蹈组有男生x 人，女生人数是男生的2倍，女生有 ( )人，男、女生共有( )人。 (2)城郊中学图书馆有科技书m本，故事书的本数是科技书 的1.8倍，那么，m+1.8m表示( )， 1.8m-m表示( )。 填一填。 2x 3x 科技书和故事书一共的本数 故事书比科技书多的数量 像上题中m+1.8m，1.8m-m如果在方程 中出现，该怎样解这样的方程呢？今天我们就来学习用这样 的方程解决问题。 二、例题讲解 共10.4元。 苹果和梨 各要2kg。 梨每千克2.8元，苹果每千克多少钱？ 从图中你获取了哪些数学信息？ 苹果和梨各买了2kg，梨每千克2.8元。 一共花了10.4元。 二、例题讲解 解：设苹果每千克x元。 2x＋2.8×2＝10.4 苹果的总价+梨的总价=总价钱 怎样列方 程？等量关系是什么？ 二、例题讲解 说一说你是怎么解的？ 2x＝4.8 x＝2.4 2x÷2＝4.8÷2 2x＋5.6－5.6＝10.4－5.6 解：2x＋5.6＝10.4 2x＋2.8×2＝10.4 先把2x看成 一个整体。 二、例题讲解 解：设苹果每千克x元。 （2.8＋x）×2＝10.4 等量关系 是什么？ 两种水果的单价总和×2＝总价钱 还可以怎么解？ 二、例题讲解 (2.8＋x)×2=10.4 x=2.4 2.8＋x=5.2 解：(2.8＋x)×2 ÷2=10.4÷2 2.8＋x－ 2.8=5.2－2.8 说一说你是怎么解的？ 先把2.8+x看 成一个整体。 二、例题讲解 2x=4.8 解：设苹果每千克x元。 2x＋2.8×2=10.4 x=2.4 2x÷2=4.8÷2 2x＋5.6－5.6=10.4－5.6 2x＋5.6=10.4 解：设苹果每千克x元。 （ 2.8＋x）×2=10.4 x =2.4 2.8＋x=5.2 （2.8＋x）×2 ÷2=10.4÷2 2.8＋x－ 2.8 =5.2－2.8 应用了乘法分配律 这两个方程之间有什么联系吗？ 二、例题讲解 怎样检验这道题是否正确？ 苹果的总价＋梨的总价＝总价钱 2×2.4 ＋2×2.8＝10.4＝总价钱 两种水果的单价总和×2＝总钱数 （2.8 ＋2.4）×2＝10.4＝总价钱 二、例题讲解 地球的表面积为5.1亿平方千米，其中，海洋面积约为陆 地面积的2.4 倍。 地球上的海洋面积 和陆地面积分别是 多少亿平方千米？ 1.从图中你获取了哪些数学信息？ 其中，海洋面积约为陆地面积的2.4 倍。 2.这道题和以前学过的应用题有什么不同之处？ 这里有两个未知数。 地球的表面积为5.1亿平方千米。 二、例题讲解 怎样设未知数呢？ 设陆地面积为x亿 平方千米，那么 海洋面积为2.4x亿 平方千米。 二、例题讲解 你能找出等量关系吗？ 陆地面积＋海洋面积＝地球表面积 根据和的等量关系列方程。 x＋2.4x＝5.1 二、例题讲解 乘法分配律 x＋2.4x＝5.1 解：(1+2.4)x=5.1 3.4x=5.1 3.4x÷3.4=5.1÷3.4 x=1.5 如何解这个方程？ 运用了什么 运算定律？ 二、例题讲解 陆地面积是1.5亿平方千米，海洋面积呢？ 5.1－1.5=3.6(亿平方千米) 也可以这样算： 2.4x =2.4×1.5=3.6(亿平方千米) 二、例题讲解 规范解答 解：设陆地面积为x亿平方千米， 那么海洋面积为2.4x亿平方千米。 陆地面积＋海洋面积＝地球表面积 x＋2.4x＝5.1 (1+2.4)x=5.1 3.4x=5.1 3.4x÷3.4=5.1÷3.4 x=1.5 答：陆地面积为1.5亿平方千米，海洋面积为3.6亿平方千米。 2.4x=2.4×1.5=3.6（亿平方千米） 三、新知应用 1. 解：设儿童票每张x元。 2x＋2×4=11 2x＋8=11 答：儿童票每张1.5元。 2x＋8－8=11-8 2x=3 2x÷2=3÷2 x=1.5 三、新知应用 2. 解：设小明今年x岁，那么妈妈今年3x岁。 3x－x＝24 2x＝24 x＝12 3x＝12×3＝36 答：小明今年12岁，妈妈今年36岁。 小明和妈妈今年分别是多少岁？ 四、课堂小结 通过这节课，你有什么新的收获？ 解形如ax±bx=c（a≠0,b≠0)的方程,先把将方 程转化为形如（a±b)x-c的方程，再求解。 五、课后作业 完成课本第78页做一做、第80页第2题。 简易方程5 人教版·五年级上册 第16课时 实际问题与方程（4） 一、新课导入 速度×时间=路程 路程÷时间=速度 路程÷速度= 时间 我们学过有关路程的问题，谁来说一说路 程、速度、时间之间的关系？ 二、例题讲解 小林家和小云家相距4.5km。周日早上9：00 两人分别从家骑 自行车相向而行，两人何时相遇？ 我每分钟骑250m。 我每分钟骑200m。 从图中你得到了哪些数学信息？ 小林每分钟骑250m,小云每分钟骑200m。 两人在相距4.5km的路上相向而行。 他们是周日早上9：00分别从家出发的。 二、例题讲解 我每分钟 骑200m。 我每分钟 骑250m。 小云 4.5km 小林 小林的路程 200m=0.2km250m=0.25km 小云的路程 小林的路程+小云的路程=总路程 你能用图把这道题的意思表示出来吗？ 二、例题讲解 小林的路程+小云的路程=总路程 0.25x+0.2x=4.5 0.45x=4.5 0.45x÷0.45=4.5÷0.45 x=10 9：00过10分钟就是9：10。 答：两人9：10可以相遇。 解:设两人x分钟后相遇。 我每分钟 骑200m。 我每分钟 骑250m。 小 云 4.5km 小林 小林的路程 200m=0.2km 250m=0.25km 小云的路程 方法一： 小林骑的路程＋小云骑的路程 =0.25×10＋0.2×10 =4.5 =总路程 检验： 二、例题讲解 我每分钟 骑200m。 我每分钟 骑250m。 小 云 4.5km 小 林 小林的路程 200m=0.2km 250m=0.25km 小云的路程 （两人每分钟骑的路程和）×x＝总路程 （0.25+ 0.2）x=4.5 0.45x=4.5 0.45x÷0.45=4.5÷0.45 x=10 9：00过10分钟就是9：10。 解:设两人x分钟后相遇。 方法二： 答：两人9：10可以相遇。 检验： 两人每分钟骑的路程和×相遇时间 ＝（0.25＋0.2）×10 ＝4.5 ＝总路程 二、例题讲解 我每分钟 骑200m。 我每分钟 骑250m。 小 云 4.5km 小林 小林的路程 200m=0.2km 250m=0.25km 小云的路程 通过画线段图可以 清楚地分析数量之 间的相等关系。 这里是用速度、 时间和路程的数 量关系来列方程。 三、新知应用 1.两列火车从相距570km的两地同时相向开出。甲车每小时 行110km，乙车每小时行80km。经过几个小时两车相遇？ 甲车的路程+乙车的路程=总路程 110x+80x=570 190x=570 190x÷190=570÷190 x=3 答：经过3小时两车相遇。 解:设经过x个小时两车相遇。 方法一： 方法二： （两车每小时行的路程和）×x＝总路程 （110+80）x=570 190x=570 x=3 解:设经过x个小时两车相遇。 三、新知应用 2.两地间的路程是455km。甲、乙两辆汽车同时从两地开出，相向而 行，经过3.5小时相遇。甲车每小时行68km，乙车每小时行多少千米？ 甲车的路程+乙车的路程=总路程 68×3.5+3.5x=455 238+3.5x=455 238+3.5x-238=455-238 3.5x=217 答：乙车每小时行62千米。 解:设乙车每小时行x千米。 方法一： 方法二： （两车每小时行的路程和）×时间＝总路程 3.5（68+x）=455 3.5（68+x）÷3.5=455÷3.5 68+x=130 解:设乙车每小时行x千米。 3.5x÷3.5=217÷3.5 x=62 68+x-68=130-68 x=62 四、课堂小结 通过这节课，你有什么新的收获？ 解决行程问题的步骤： 1.画线段图分析数量关系，找出等量关系； 2.根据速度、时间和路程三者之间的数量关系列方程解答。 五、课后作业 完成课本练习十七第82页第13题。 简易方程5 人教版·五年级上册 第17课时 练习十七 P80 每个都是0.12元， 一共卖了1.8元。 我们收集了易拉罐和 饮料瓶，易拉罐有6个。 饮料瓶有几个？ 易拉罐的单价×数量+饮料瓶的单价×数量=一共卖的钱数 2. 解：设饮料瓶有x个。 0.12×6+0.12×x=1.8 0.72+0.12x=1.8 0.12x=1.08 x=9 答：饮料瓶有9个。 一、复习巩固 实际问题与方程知识点1 二、课堂练习 P81 8.两个相邻自然数的和是 97 ，这两个自然数分别是多少？ 解：设较小的自然数是x，则较大的自然数是x+1。 x +x+1=97 2x+1=97 x=48 x+1=48+1=49 答：这两个自然数分别是48、49。 二、课堂练习 P81 9.上午运了3次，下 午要运多少次才能 运完？ 解：设下午要运x次才能运完。 （3+x）×5=35 15+5x=35 5x=20 x=4 答：下午要运4次才能运完。 二、课堂练习 P82 解：设乙队每天开凿x米。 （12.6＋x）×25=675 12.6＋x=27 x=14.4 答：乙队每天开凿14.4米。 13.两个工程队同时开凿一条675m长的隧道，各从一端相向施 工，25天打通。甲队每天开凿12.6m，乙队每天开凿多少米？ 二、课堂练习 P82 15*.看图列方程，并求出方程的解。 3x=100+x 解:3x-x=100+x-x 2x=100 x=50 二、课堂练习 P82 箱子里装有同样数量的乒乓球和羽毛球。 每次取出5个乒乓球和3个羽毛球,取了几次以 后,乒乓球没有了,羽毛球还剩6个。一共取了 几次?原来乒乓球和羽毛球各有多少个? （1）根据“相同数量”,可得到等量关系式：“乒乓球的数量=羽毛球的数量” （2）再由取的次数是一样的,可以设取的次数为x,乒乓球的个数为5x,羽毛球的个 数为3x+6,得方程5x=3x+6。 二、课堂练习 P82 规范解答 解:设一共取了x次。 　 5x=3x+6 5x-3x=3x+6-3x 2x=6 x=3 原来乒乓球有5×3=15(个) 羽毛球有3×3+6=15(个) 答:一共取了3次。原来乒乓球有15个,羽毛球也有15个。 解决行程问题的有什么步骤？ 1.画线段图分析数量关系，找出等量关系； 2.根据速度、时间和路程三者之间的数量关系列方程解答。 知识总结 三、课后作业 完成练习十七第80-82页第1、5、14题。 简易方程5 人教版·五年级上册 第19课时 练习十八 × × √ √ P84 一、复习巩固 方程的意义 知识点1 3.8+x=6.3 x-7.9=2.6 解：3.8+x-3.8=6.3-3.8 x=2.5 解：x-7.9+7.9=2.6+7.9 x=10.5 P84 2.5x=14 x÷3=1.2 解：2.5x÷2.5=14÷2.5 x=5.6 解：x÷3×3=1.2×3 x=3.6 2.解下列方程。 解方程 知识点2 二、课堂练习 3.4x-48=26.8 2x-97=34.2 解：3.4x-48+48=26.8+48 3.4x=74.8 x=22 解：2x-97+97=34.2+97 2x=131.2 x=65.6 42x+25x=134 13（x+5）=169 解： 67x=134 67x÷67=134÷67 x=2 解： 13x+65=169 13x+65-65=169-65 13x=104 x=8 二、课堂练习 P84 3. 我运动以后每分钟心跳130 次，比运动前多55次。 他运动前每分钟心跳多少次？ 解：设他运动前每分钟心跳x次。 x+55=130 x+55-55=130-55 x=75 答: 他运动前每分钟心跳75次。 二、课堂练习 4.太阳系的八大行星中，离太阳最近的是水星。地球绕 太阳一周是365天，比水星绕太阳一周所用时间的4倍还 多13天。水星绕太阳一周是多少天？ 解：设水星绕太阳一周是x天。 4x+13=365 4x+13-13=365-13 4x=352 4x÷4=352÷4 x=88 答：水星绕太阳一周是88天。 P84 二、课堂练习 5.2002年8月15 日，浙江省第一艘自行制造的载质量达 25000吨的巨轮“阿斯娜”号从造船基地下水，驶向大海。 哇！它的载质量比我们的 8 倍 还多 1000 吨。 解：设小轮船的载重量是x吨。 8x+1000=25000 8x+1000-1000=25000-1000 8x=24000 8x÷8=24000÷8 x=3000 答：小轮船的载重量是3000吨。 3000 P84 二、课堂练习 5.小明和小红在校门口分手，7分钟后他们同时到家。小明平均每分钟 走45 m，小红平均每分钟走多少米？ P85 解：设小红平均每分钟走xm。 45×7+7x=560 解： 315+7x=560 315+7x-315=560-315 7x=245 7x÷7=245÷7 x=35 答：小红平均每分钟走35米。 二、课堂练习 P85 9* 他们两人分别有多少颗玻璃球？ 解：设小丽有x颗，小亮有2x颗。 2x-3=x+3 2x-3-x=x+3-x x-3=3 x-3+3=3+3 x=6 2x=2×6=12(颗） 答：小丽有6颗，小亮有12颗。 列方程解决实际问题 有哪些步骤？ 1.找出未知数，用字母x表示； 2.分析实际问题中的数量关系，找出等量关系，列方程； 3.解方程并检验作答。 知识总结 三、课后作业 完成练习十八第85页第6、7题。 简易方程5 人教版·五年级上册 第五单元复习提升 一、学习目标 知识技能：加深理解简易方程的意义和作用，会解简易方程。 问题解决：能够熟练分析应用题中数量关系的特点，适当的 选择解题方法。 数学思考：让学生独立思考、自主探究、合作交流，加深对 列方程解题的认识。 情感态度：培养总结、归纳的学习能力，养成善于思考总结的 习惯。 二、学习重难点 学习重点：回顾和整理解方程 和用方程解决问题。 学习难点：分析应用题中数量关 系的特点，适当的选择解题方法。 三、知识点汇总 简易方程 用字母表示数 解决问题 表 示 一 个 数 方程 方 程 的 意 义 表 示 数 量 关 系 等 式 的 性 质 方 程 的 解 法 方 程 的 应 用 1.用字母表示数 用 字 母 表 示 数 1.用字母表示一个数。 2.用字母表示变化的数及数量关系。 3.用字母表示运算律。 三、知识点汇总 2.方程的意义 方程的意义 含有未知数的等式叫做方程 等式 含有未知数 判断依据 三、知识点汇总 等式的性质 性质1： 等式两边加上或减去同 一个数，左右两边仍然 相等。 性质2： 等式两边乘同一个数， 或除以同一个不为0的 数，左右两边仍然相等。 3.等式的性质 三、知识点汇总 方程的 解法 方程的解 解 方 程 使方程左右两边相等的未知数的值， 叫做方程的解。 形如ax=b的方程 解：ax÷a=b÷a x=b÷a 形如a－x=b的方程 解：a－x+x=b+x b+x=a x=a-b 形如ax±b=c的方程把ax看成一个整体 形如a(x±b)=c的方程把(x±b)看成一个整体 4.方程的解法 三、知识点汇总 5.方程的应用 列 方 程 解 应 用 题 应用ax±ab=c解决实际问题 应用x±bx=c解决实际问题 应用ax±bx=c解决实际问题 三、知识点汇总 列方程解决实际问题的步骤： (1)找出未知数，用字母x表示； (2)分析实际问题中的数量关系，找出等量关系， 列方程； (3)解方程并检验作答。 三、知识点汇总 四、问题解决 1.解下列方程。 x+4.8=7.2 x-6.5=3.2 解：x+4.8-4.8=7.2-4.8 x=2.4 解：x-6.5+6.5=3.2+6.5 x=9.7 四、问题解决 x÷8=0.4 6x+18=48 解：x÷8×8=0.4×8 x=3.2 解：6x+18－18=48－18 6x=30 x=5 四、问题解决 3(x+2.1)=10.5 12x-9x=8.7 解：3(x+2.1)÷3=10.5÷3 x+2.1 =3.5 x+2.1-2.1=3.5-2.1 x=1.4 解：3x=8.7 3x÷3=8.7÷3 x=2.9 四、问题解决 2.列方程解决实际问题。 哈，93kg！这两个月我坚 持锻炼，体重减少了3kg。 两个月前，他的 体重是多少千克？ 解：设两个月前他的体重为x千克。 x-3=93 x-3+3=93+3 x=96 答：两个月前他的体重是96千克。 （1） 四、问题解决 （2） 这条街一共有多 少盏路灯？ 解：设这条街一共有x盏路灯. 5x=140 5x÷5=140÷5 x=28 答：这条街一共有28盏路灯。 四、问题解决 x 3.5x （3） 解：设小鹿的高度为xm，那么 我长颈鹿的高度为3.5xm。 3.5x－x=3.65 2.5x=3.65 2.5x÷2.5=3.65÷2.5 x=1.46 答：小鹿的高度为1.46m。 完成课本第84页练习十八第1、2题。 五、课后作业