人教五年级下册数学总复习

人教五年级下册数学总复习

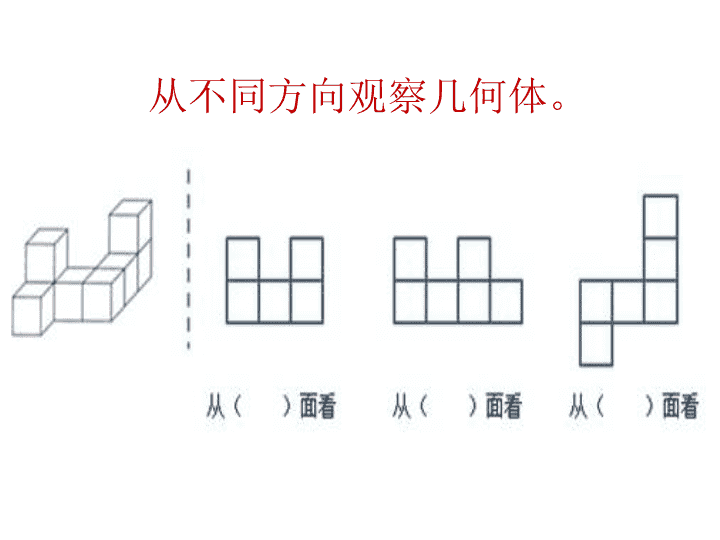
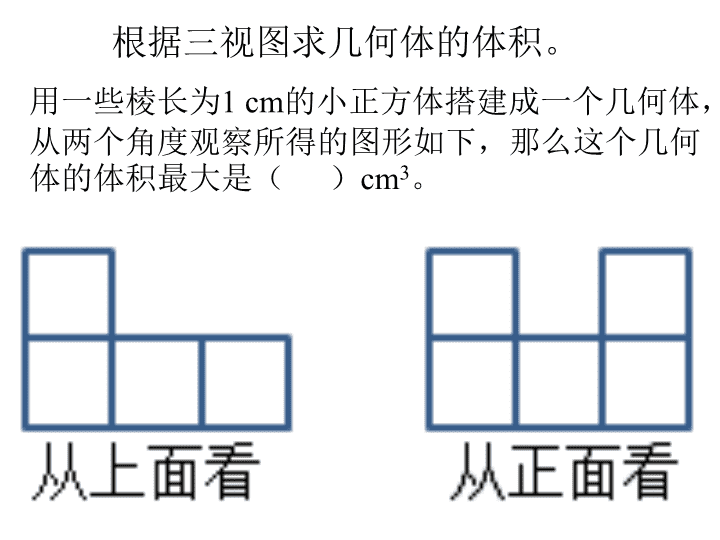
观察物体 1 、从不同方向观察几何体并确定看到的平面图形。 2 、从不同方向观察看到的平面图形并确定还原几何体。 从不同方向观察几何体。 用一些棱长为 1 cm 的小正方体搭建成一个几何体， 从两个角度观察所得的图形如下，那么这个几何 体的体积最大是（      ） cm 3 。 根据三视图求几何体的体积。 如图，再添一个同样大小的小正方体，小明就把 图 1 小丽搭的积木变成了图 2 六种不同的形状。 （ 1 ）从左面看，小明搭的积木中（     ）号和（     ）号的形状和小丽搭的是相同的； （ 2 ）从正面看，小明搭的积木中，形状相同的是（    ）号和（     ）号，或者是（     ）号和（    ）号。 从不同方向观察几何体，并确定所看到的平面图形的形状。 一个用小正方体搭成的几何体，下面是它的两个不同方向看到的形状，要符合这两个条件，最少需要摆（   ）块，最多能摆（   ）块，共有（   ）种摆法。 选择 一堆同样大小的正方体拼搭图形，从不同方 向看到的图形分别如图，那么至少有（     ）块 同样的正方体。 A.5                B.6                C.7                D.8 从正面看是图（ 1 ）的立体图形有（      ）； 从左面看是图（ 2 ）的立体图形有（      ）； 从左面和上面看都是由两个小正方形组成的 立体图形是（       ）。 A.7                    B.8                    C.9                    D.10 5 ．有几堆摆好的小方块，从三个不同的方向观察看到的形状如下图，这里至少有（     ）个小方块。 因数与倍数 除尽 整除 2 、 5 、 3 倍数的特征 自然数 1 质数 合数 质因数 倍数 因数 因数与倍数 偶数 奇数 因数的应用 数的奇偶性的应用 易混概念对比 如果甲数是乙数的 5 倍，那么，乙数一定 是甲数的倍数。（ ） 倍的概念比倍数要广，倍可以适用于小数、分数和整数，而倍数只适用于整数。例如： 16 ÷ 8=2 我们就说 16 是 8 和 2 的倍数，也可以说 2 是 8 是 16 的因数。 1.6÷0.8=2 我们就说 1.6 是 0.8 的 2 倍，但不能说 1.6 是 0.8 的倍数。 也就是说因数倍数关系只能在都是整数的情况下说的。 易混概念对比 质数 是一个具体的数，它是相对于一个数的因数的个数而言的。 质因数 也是一个具体的数，必须是一个质数它是一个合数的因数。 分解质因数 是把一个一个合数分解成几个质数相乘形式的过程。 互质数 是公因数只有 1 的两个数。 自然数 按 是不是 2 的倍数 分为： 偶数 和 奇数 偶数： 是 2 的倍数的数，即 双数，最小的偶数是 0 奇数： 不是 2 的倍数的数，即 单数，最小的奇数是 1 自然数 按 因数的个数 分为： 质数、合数 和 1 质数： 只有 1 和它本身两个因数的数。 如： 2 、 3 、 5 、 7 、 11 、 13 、 17 、 19…… （熟记 100 以内的质数） 合数： 除了 1 和它本身以外，还有其他因数的数。 如： 4 、 6 、 8 、 9 、 10 、 12 、 14 、 15…… （至少有 3 个因数） 1 ： 既不是质数也不是合数 互质数特殊的判断方法 ① 1 和任意自然数互质。 ②2 和任意奇数都是互质数。 ③ 相邻两个自然数都是互质数。 ④ 相邻的两个奇数都是互质数。 ⑤ 不相同的两个质数是互质数。 ⑥ 当一个数是合数，而另一个数是质数时，若合数不是质数的倍数，一般情况下这两个数也是互质数。 2. 出示判断题： （ 1 ）自然数中，除了奇数就是偶数。（ ） （ 2 ）所有的奇数都是质数。 （ ） （ 3 ）所有的合数都是偶数。 （ ） （ 4 ）自然数中，除了质数就是合数。（ ） （ 5 ）质数与质数的积还是质数。 （ ） （ 6 ）一个数越大，它的因数的个数就越多。 （ ） 注意：奇数里既有质数也有合数还有 1 。 质数里除了 2 以外都是奇数。 偶数里除了 2 以外全是合数。 3. 奇数和偶数的运算性质 奇数 ± 奇数 = 偶数 偶数 ± 偶数 = 偶数 奇数 ± 偶数 = 奇数 奇数 × 奇数 = 奇数 偶数 × 偶数 = 偶数 奇数 × 偶数 = 偶数 2 的倍数的特征： 个位上是 0 、 2 、 4 、 6 、 8 的数。 3 的倍数的特征： 各位数的和是 3 的倍数 5 的倍数的特征： 个 位上是 0 或 5 的数。 同时是 2 和 5 的倍数的特征： 个位上是 0 ，即是 10 的倍数。 同时是 2 和 3 的倍数的特征： 个位上是 0 、 2 、 4 、 6 、 8 ，且各位数的和是 3 的倍数，即是 6 的倍数。 同时是 3 和 5 的倍数的特征： 个位上是 0 或 5 ，且各位数的和是 3 的倍数，即是 15 的倍数。 同时是 2 、 3 、 5 的倍数的特征： 个位上是 0 ，即是 30 的倍数。 同时是 2 、 3 倍数的最小数是（ ）。 同时是 2 、 5 倍数的最大两位数（ ）。 同时是 3 、 5 倍数的最大两位奇数（ ）。 同时是 2 、 3 和 5 倍数的最小三位数（ ）。 6 90 75 120 活学活用 1 、小华买了 1 支铅笔、 2 块橡皮、 2 个练习本付了 10 元钱，售货员找给他 5 角钱 . 小华看了看 1 支铅笔的价钱是 8 角，就说：“叔叔，您把账算错啦 . ” 想一想，小华为什么这么快就知道账算错了 ? 2 、如果要把 33 个学生分成 5 个队，要求每个队的人数都是奇数，你能做到吗？为什么？ 3 、傍晚开电灯，小虎淘气，一连拉了 7 下开关 . 请你说说这时灯是亮了还是没亮 ? 4 、一个长方形的面积是 24 平方厘米，把这个长方形画出来（长和宽都是整厘米），共有多少种画法？ 5 、 24 个同学排队做操，共有多少种排法？每排各站多少人？ 长方体 正方体 长方体、正方体的特征 长方体、正方体的表面积 长方体、正方体的体积 顶点 面 棱 意义 单位、进率 计算 意义 计算 长方体和正方体 长方体和正方体的特征 形体 相同点 不同点 联系 面 棱 顶点 面的 形状 面的 面积 棱长 长方体 正方体 6 个 12 条 8 个 6 个面都是长方形（特殊情况有两个相对的面是正方形，其余 4 个面完全相同） 6 个面都是正方形 相对的两个面完全相同 6 个面完全相同 相对的棱的长度相等 12 条棱的长度都相等 正方体是一种特殊的长方体 表面积： 长方体或正方体 6 个面的总面积 体积： 物体所占空间的大小 容积： 容器所能容纳物体体积的大小 S 长 = （长 × 宽 + 长 × 高 + 宽 × 高） ×2 V 长 ＝ 长 × 宽 × 高 长方体、正方体的棱长总和表面积、体积、容积 和体积算法一样，计算容积一般用体积单位，计算液体的体积是用升（ L ）和毫升（ ml ）作单位（但要从里面量，所以一个容器的容积一般要比它的体积小） 棱长总和： 长方体或正方体 12 条棱的总长 C 长 = （长 + 宽 + 高） ×4 或 = 底面周长 ×2+ 高 ×4 C 正 = 棱长 ×12 S 正 = 棱长 × 棱长 ×6 V 正 = 棱长 × 棱长 × 棱长 V ＝ 底面积 × 高 或 = 横截面积 × 长 解决问题时要认真分析算几个面，算哪些面的面积？ 做 一 做 1 、一个长方体的底面积是５６平方厘米，高是８厘米，求它的体积。 根据Ｖ＝ Sh, 可以这样计算： ５６ × ８＝４４８（立方厘米） 答：它的体积是４４８立方厘米。 ２、一根长方体木料，长５米，横截面的面积是 0.06 平方米。这根木料的体积是多少？ ０ . ０６平方米 长５米 长５米 ０ .06×5 ＝ 0.3 （立方米） 答：它的体积是 0.3 立方米。 根据Ｖ＝ Sh, 可以这样计算： ※ 长方体和正方体的特征 （ 1 ）根据长方体和正方体的关系填空 ( 填正方体或长方体 ) 。 （ 2 ）一个长 5 厘米 , 宽 3 厘米 , 高 4 厘米的长方体木块 , 要削成一个最大的正方体 , 正方体棱长是多少厘米 ? ( ) ( ) 长方体 正方体 5 4 3 3 3 3 长方体的长、宽、高都变为原来的 2 倍，它的表面积和体积发生了什么变化？ 长方体的长、宽、高都变为原来的 2 （ n ） 倍，它的表面积跟着变为原来的 4 （ n 2 ） 倍，体积也跟着变为原来的 8 （ n 3 ） 倍。 1 、 正方体的棱长扩大 2 倍，其棱长和扩大 （ ） 倍，表面积扩大 （ ） 倍，体积扩大 （ ） 倍； 2 、 长方体的长宽高同时扩大 3 倍，其棱长和扩大 （ ） 倍，表面积扩大 （ ） 倍，体积扩大 （ ） 倍 不规则物体体积 = 总体积 － 水的体积 （物体和水的） 不规则物体体积 = 底面积 × 上升的高度 6 完全相同 12 长度相等 8 6 都相同 12 都相等 8 正方体的 11 种展开图。 图（ 1 ） 图（ 2 ） 图（ 3 ） 图（ 4 ） 图（ 5 ） 图（ 6 ） 第一类：中间四连方，两侧各有一个，共 6 种 第二类：中间三连方，一侧有一个、一侧有二个，共 3 种 图（ 7 ） 图（ 8 ） 图（ 9 ） 第三类：中间两连方，两侧各有 2 个，只有 1 种 图（ 10 ） 第四类：两排各有 3 个，只有 1 种 图（ 11 ） 与右面正方体一致的展开图是（ ）。 B 1 2 3 1 2 3 2 3 1 1 2 3 C B A 下面哪个图形可以折叠成一个正方体，请在对应的括号里打“√”。 （ ） （ ） （ ） （ ） （ ） （ ） （ ） （ ） （ ） （ ） √ 1 、一个木箱的体积就是它的容积 。 2 、长方体是特殊的正方体。 3 、棱长 6 分米的正方体，它的表面积和体积相等。 4 、用 4 个棱长 1 厘米的小正方体可以拼成一个大正方体。 5 、体积单位间的进率都是 1000 。 6 、把一个正方体的橡皮泥捏成一个长方体后虽然它的形状变了，但是它所占空间的大小不变。 7 、正方体的棱长扩大 2 倍，它的体积就扩大 6 倍。 8 、 长方体的六个面一定是长方形 。 9 、 正方体的六个面面积一定相等 。 10 、 一个长方体 ( 非正方体 ) 最多有四个面面积相等 。 11 、 相交于一个顶点的三条棱相等的长方体一定是正方体。 数学诊所 8.3 立方米 =( 　　　　 ) 立方米 ( 　　　 ) 立方分米 　　　　 =( 　　　　 ) 立方分米 =( 　 　　 ) 立方厘米 4.05 立方分米 =( 　　　 ) 立方厘米　　　　　　　　 　 2.8 立方分米 =( 　　　 ) 立方分米 ( 　　　 ) 立方厘米 200 立方厘米 =( 　　　　 ) 立方分米 9034000 立方厘米 =( 　　　　 ) 立方米 0.2 4050 9.034 8 300 8300 8300000 2 800 快速切换 1 、计量一个长方体的棱长用（ ）单位，计量它的表面积用（ ）单位，计量它的体积用（ ）单位。 2 、 用棱长为 2 厘米的小正方体拼一个稍大一些的正方体至少需要（ ）个小正方体。 3 、一辆汽车油箱的容积大约是 72 （ ）。 4 、数学书的体积大约是 320 （ ）。 5 、 至少需要（    ）厘米长的铁丝，才能做一个底面周长是 18 厘米，高 3 厘米的长方体框架。 6 、一个长方体纸箱，长和宽都是 3 分米，高是 4 分米，做这样的一个纸箱需要纸板 ( ) 平方分米，它的容积是 ( ) 立方分米。 7 、 有一根 150cm 长的铁丝，用这根铁丝焊成了一个正方体的框架，还剩铁丝 6cm 。这个正方体框架的棱长是（ ）厘米。 思维快车 长度 面积 体积 升 立方厘米 48 66 36 12 8 棱是用角钢做的 底面用铁板做成 四周用玻璃做成 （ 5 ）这个鱼缸能装多少升水？ 棱长和 底面积 侧面积 体积 小 小 设 计 师 结合本单元整理的概念 , 说一说下列问题实际要求什么 ? 容积 （ 2 ）做这个鱼缸要用多少平方分米的铁皮？ （ 3 ）做这个鱼缸要用多少平方分米的玻璃？ （ 4 ）这个鱼缸占多少空间？ （ 1 ）做这个鱼缸要用多少分米的角钢？ 棱是用角钢做的 底面用铁板做成 四周用玻璃做成 （ 5 ）这个鱼缸装了多少升水？ 棱长和 :(6+3+4)×4= 底面积 :6 ×3= 侧面积 :(6 ×4+3×4) ×2= 体积 :6 ×3×4= 小 小 设 计 师 给你具体数据你会计算吗？在计算中玻璃、钢板等厚度忽略不计 ( 只要说算式就可以 ) （ 2 ）做这个鱼缸要用多少平方分米的铁皮？ （ 3 ）做这个鱼缸要用多少平方分米的玻璃？ （ 4 ）这个鱼缸占多少空间？ （ 1 ）做这个鱼缸要用多少分米的角钢？ 条件 : 长： 6 dm 宽： 3 dm 高： 4 dm 水深： 3dm 水的体积 :6 ×3×3= 四周用玻璃做成 棱是用角钢做的 底面用铁板做成 典型问题 1 、 2 、一盒饼干长 20 厘米，宽 15 厘米，高 30 厘米，现在要在它的四周贴上商标纸，如果商标纸的接头处是 4 厘米，这张商标纸的面积是多少平方厘米？ 3 、做 一节长 120 厘米，宽和高都是 10 厘米的通风管，至少需要铁皮多少平方厘米？ 4 、 一个房间的长 6 米，宽 3.5 米，高 3 米，门窗面积是 8 平方米。现在要把这个房间的四壁和顶面粉刷水泥，粉刷水泥的面积是多少平方米？ 5 、一个长方体鱼缸，长８０厘米，宽６０厘米，深４０厘米，把一块长３０厘米，宽２４厘米，高１６厘米的铁块浸入在水中，水面将上升多少厘米 ? 8 、一个长方体鱼缸，长８０厘米，宽６０厘米，装满水后深４０厘米，把两块底面边长为２０厘米，高为 9 ０厘米的铁块直立在水中，溢出水的体积是多少升？ 6 、一个长方体鱼缸，长８０厘米，宽６０厘米，深４０厘米，把一块石头完全浸入水中，水面升高了 5 厘米，石头的体积是多少立方厘米 ? 7 、一个长方体鱼缸，长８分米，宽６分米，深４分米，里面装有 144L 水。现在把一个石头完全浸入水中时，量的水深 32 厘米。石头的体积是多少立方厘米 ? 9 、一块长方形铁皮长 40 厘米，宽 30 厘米，如 图， 从四个角上剪去边长是 3 厘米的正方形，然后做成盒子，这个盒子的表面积和体积各是多少？ 10 、一个棱长为１分米的正方体木块切割成棱长是１厘米的小正方体，把切成的所有正方体紧挨着排成一排，可以排多少米？ 12 、把三个完全一样的正方体拼成一个长方体后，长方体的棱长总和是 80 厘米，拼成的长方体的表面积和体积各是多少？ 11 、一个棱长是 20 分米的正方体玻璃容器装满水，然后把水倒入一个长 25 分米，宽 16 分米的长方体水箱内，求这时水深多少分米？ 甲 乙 取出石块后 2.1dm 1.8dm 13. 图中有两个完全一样的长方体水箱，水箱的底面积是 2 平方分米，请结合图中所给信息求出甲箱中石块的体积是多少？ 2×(2.1-1.8)=0.6 （ dm ³ ） 答：石块的体积是 0.6dm ³ 。 14. 有一个长方体，底面是一个正方形，高 18cm ，侧面展开正好是一个正方形。这个长方体的体积是（ ） cm³ 。 18cm 18cm 18cm 16. 把棱长是 1 厘米的小正方体拼摆在一起。如果从右面看，所看到的图形面积是 ( ) 平方厘米，体积是（ ）立方厘米。 15 、 17. 一个棱长为 2cm 的正方体，在它的一个角上挖掉一个棱长为 1cm 的小正方体，它的表面积是 （     ） cm² 。 18 、用 3 个长 5cm, 宽 4cm, 高 3cm 的长方体木块，拼成一个表面积最小的长方体。这个长方体的表面积是多少平方厘米？ 5cm 4cm 3cm 3cm 2cm 6cm 6cm 19 、有一个形状如图的零件，由一个长方体和一个 正方体组合而成。长方体的长和宽都是 6cm ，高是 3cm ，正方体的棱长是 2cm 。求这个零件的表面积。 20 ．由 27 个棱长为 1cm 的小正方体组成一个棱长为 3cm 的大正方体，若自上而下去掉中间的 3 个小正方体（如图所示），则剩下的几何体的表面积是多少平方厘米？ 3×3×6 － 1×1×2 ＋ 3×1×4 =54 － 2 ＋ 12 =64 （ cm² ） 答：剩下的几何体的表面积是 64 平方厘米。 21 ．从一个大长方体上切下一个体积是 128 立方厘米的小长方体（如图）。原来大长方体的体积是多少立方厘米？ 22cm 8cm 切下部分 128÷8×22 =16×22 =352 （立方厘米） 答：原来大长方体的体积是 352 立方厘米。 22. 一个密封的长方体容器里面装有一些水，水深 9 厘米，如果把这个容器的右面做底，这时容器内的水深多少厘米？ 36 10 12 36 10 12 36×10×9=3240 （ cm3 ） 3240÷(12×10)=27 （ cm ） 答：容器内的水深 27 厘米。 1 、把一根长 30 厘米的长方体木料锯成 3 段 ( 如图 ), 表面积比原来增加了 20 平方厘米 , 这根木料原来的体积是多少立方厘米 ? 2 、 一个长方体木块被截成两个完全相同的正方体后，棱长之和增加了 24 厘米。求原来长方体的 棱长总和 是多少厘米？ 3 、至少需要多少厘米长的铁丝，才能做一个底面周长是 18 厘米，高 3 厘米的长方体框架？ 拓展题： 难度系数：★★ ★★★ 4 、一个底面是正方形的长方体，把它的侧面展开后得到一个长是 12 厘米，宽是 20 厘米的长方形。求这个长方体的体积是多少？ 20 12 20 3 3 拓展题： 难度系数：★★★ ★★ 5 、一个长方体，如果高增加 3 厘米，就成为一个正方体。这时表面积比原来增加了 96 平方厘米。原来的长方体的体积是多少立方厘米？ 6 、一个长 40 厘米的长方体，它的横截面是正方形，如果长增加 5 厘米，表面积就增加 80 平方厘米，原长方体的体积是多少？ 难度系数：★★★★ ★ 难度系数：★★★★ ★ 分数的意义和性质 分数 分数的意义 分数单位 分子分母的意义 分数与除法的关系 分数大小的比较 分数的分类 真分数 假分数 整数 带分数 分数的基本性质 约分 通分 求一个数是另一个数的几分之几 分数和小数的互化 表示把单位 “ 1 ” 平均分成 4 份，取其中 3 份。 还表示把 3 平均分成 4 份，取其中 1 份。 分数的意义 表示 3 的 。 表示 3 个 。 把单位“ 1” 平均分成若干份，表示这样的一份或者几份的数，叫做分数。 把 1 米平均分成 4 份，表示这样 3 份的数 表示 1 米的 把 3 米平均分成 4 份，表示这样 1 份的数 表示 3 米的 米 1 米 3 米 米 单位“ 1” 表示： 一个物体、一些物体等都可以看作一个整体，一个整体可以用自然数 1 来表示，通常把它叫做“ 1” 。 分数单位表示： 把单位“ 1” 平均分成若干份，表示其中一份的数叫分数单位。 单位 “ 1 ” 与分数单位的区别 1. 表示把单位“ 1” 平均分成 5 份，取其中 3 份的分数是（ ），它的分数单位是（ ），再添上（ ）个这样的分数单位就是单位“ 1” 。 2. 里面有（ ）个 。 （ ）里面有 3 个 。 3 个 是（ ）。 比比两条线段哪个长？ 1 3 1 4 写出数轴上点 A 、点 B 、点 C 、点 D 表示的分数 5. 请在一条数轴上表示下列分数： 分数与除法的关系 工程队修一条 5 千米长的公路， 7 天修完， （ 1 ）平均每天修这条公路的（ —— ）千米； （ 2 ）平均每千米要修（ —— ）天； （ 3 ）平均每天修的占这条公路的（ —— ）。 工程队修一条 5 千米长的公路， 7 天修完， 平均每 天 修这条公路的（ —— ） 千米 ； 总千米 ÷ 总天数 = 每份数 5 ÷ 7 = （千米） 工程队修一条 5 千米长的公路， 7 天修完， 平均每 千米 要修（ —— ） 天 ； 总天数 ÷ 总千米 = 每份数 7 ÷ 5 = （天） 1 工程队修一条 5 千米长的公路， 7 天修完， 平均 每天 修的占 这条公路 的（ —— ）。 1 ÷ 7 = 工程队修一条 5 千米长的公路， 7 天修完， （ 1 ）平均每天修这条公路的（ ）千米； （ 2 ）平均每千米要修（ ）天； （ 3 ）平均每天修的占这条公路的（ ）。 1 把 4 米长的钢筋平均截成 5 段， 每 段 长（ ） 米 ？ 总米数 ÷ 总段数 = 每份数 4 ÷ 5 = （米） 每段 是钢筋 全长 的（ —— ） 1 ÷ 5 = 一个班有学生 50 人，其中 13 人被评为 “ 三好学生 ” 。 “ 三好学生 ” 占 全班人数 的（ —— ）。 13 ÷ 50 = 小结：分数与除法的关系 分数可以表示整数除法的商，在表示整数除法时，要用除数作分母，用被除数作分子。 用关系式表示： 被除数 ÷ 除数 = ———— 用字母可以表示成： a÷b= —— 因为除数不能等于 “ 0 ” ，所以 b 也不能等于 “ 0 ” 。 被除数 除数 a b 分数与除法是有区别的。除法是一种运算，它有运算符号，是一个算式；而分数是一个 “ 数 ” ，当它在除法算式中的时候，它可以表示除法算式的结果。 小结： 当一个量不能用整数个计量单位来表示时，可以用分数来表示。即分数可以表示一个量，分数还可以表示两个量之间的关系。 用分数表示下列除法算式的商。 6÷7= 11÷9= 15÷17= a÷b= 下图是长方形，它的面积是 5 平方厘米。请你用阴影表示出 5 8 平方厘米的部分 5 平方厘米 5 平方厘米 5 平方厘米的 1 8 5 平方厘米 1 平方厘米的 5 8 填空 把一条 4 米长的木材平均分成 5 段，每段是这条木材的（　　），每段是（　　）米。 把一条 5 米长的木材平均分成 6 段，每段是这条木材的（　　），每段是（　　）米。 把一条 7 米长的木材平均分成 8 段，每段是这条木材的（　　），每段是（　　）米。 把一根绳子对折 2 次，这时每段绳子是全长的（　）。 把一根绳子对折 3 次，这时每段绳子是全长的（　）。 把一根绳子对折 5 次，这时每段绳子是全长的（　）。 真分数和假分数 意义 特征 真分数 分子比分母小的分数 真分数小于 1 假分数 分子比分母大或分子和分母相等的分数 假分数都大于或等于 1 1. 在分数 中， 当 a （ ）时，它是真分数； 当 a ( ) 时，它是假分数； 当 a （ ） 时，它等于 1 ； 当 a ( ) 时，它就是这个分数的分数单位。 2 ．分数单位是 的最小真分数是 ( ) ，最小假分数 是（ ）。 a 9 大于 9 或等于 9 小于 9 等于 9 等于 1 ４　的分数单位是（　　），去掉（　　）个 这样的分数单位就是最小的合数。 ２ ７ 　　的分数单位是（　　），再添（　　） 个这样的分数单位就是最小的质数。 ７ ８ 在　　中， a 是不为 0 的自然数。 a 5 （真分数？假分数？最小假分数？最大真分数？） 填空 1. 分数的基本性质 分数的分子和分母同时乘或者除以相同的数（ 0 除外），分数的大小不变。这叫做分数的基本性质。 2. 约分 把一个分数化成和它相等，但分子、分母都比较小的分数，叫做约分。 3. 通分 把异分母分数分别化成和原来分数相等的同分母分数，叫做通分。 4. 最简分数 分子、分母只有公因数 1 的分数，叫做最简分数。 分数的基本性质 占单位 “ 1 ” 的一半不够 占单位 “ 1 ” 的一半多 ﹤ 不用通分的方法，比较分数的大小。 因为 ﹥ 所以（ 1 — ） ﹤（ 1— ) ﹤ 分数 的分子加上 8 ，要使分数 大小不变，分母应该（ ）。 0.6=( ) ÷25= 12 （ ） 3 5 或 3÷5 一个分数的分子扩大 20 倍，分母缩小 20 倍，结果如何？ A = 2×2×2×3 B = 2×2×3×3 A 和 B 的最大公因数 = A 和 B 的最小公倍数 = 2 × 2 × 3 =12 2 × 2 × 3 ×2×3=72 两个数的最小公倍数 = 它们的最大公因数 × 它们独有的因数 两个数的乘积最小公倍数 = 它们的最大公因数 × 它们的最小公倍数 ② 求出 1 和 7 、 8 和 9 、 9 和 16 的最大公因数 . ① 求出 4 和 8 、 16 和 32 、 17 和 34 的最大公因数 . 4 和 8 的最大公因数： 4 16 和 32 的最大公因数： 16 17 和 34 的最大公因数： 17 1 和 7 的最大公因数： 1 8 和 9 的最大公因数： 1 9 和 16 的最大公因数： 1 当两个数成 倍数关系 时，较小的数就是它们的最大公因数。 当两个数只有公因数 1 时，它们的最大公因数也是 1 。 互质数 找出下列每组数的最小公倍数。 3 和 6 2 和 8 5 和 6 4 和 9 3 和 6 的最小公倍数是 6 。 2 和 8 的最小公倍数是 8 。 5 和 6 的最小公倍数是 30 。 4 和 9 的最小公倍数是 36 。 两个数是互质数关系，它们的最小公倍数就是它们的乘积。 两个数是倍数关系，它们的最小公倍数就是较大的数。 同时熟记 7 、 11 、 13 、 17 、 19 等数的倍数 及 11—20 所有数的平方数以提高计算速度。 求三个数的最小公倍数的特殊规律： 当三个数两两互质时，最小公倍数是这三个数的积； [2 ， 7 ， 9]= 126 当三个数都成整倍数关系时，最大的数就是最小公倍数； [18 ， 6 ， 54]= 54 当三个数中有两个数成倍数关系时，那么求三个数的最小公倍数就可转化为求这两个数中较大者与第三个数的最小公倍数等。 [18 ， 6 ， 27] [18 ， 27]=108 把下面每组中的两个分数通分。 2 3 和 1 4 1 6 和 7 12 3 10 和 8 15 解决问题 小船最初在南岸，从南岸驶向北岸，再从北岸返回南岸，不断往返。 （ 1 ）小船摆渡 11 次后，船在南岸还是北岸？为什么？ （ 2 ）有人说摆渡 100 次后，小船在北岸，他的说法对吗？为什么？ 分析： 在两点间行走，走 奇数次后 到与起点 相对处 ，走 偶数次后 回到 起点处 。 北京站是 104 路和 103 路电车的起发站。 104 路每 3 分发一次车， 103 路每 8 分发一次车，这两路电车同时发车以后，至少再过多少分又同时发车？ 分析： 104 路电车每 3 分发一次车，每次发车时间一定是 3 的倍数，即第二次发车与第一次发车间隔 3 分，第三次发车与第一次发车间隔 6 分，而 103 路电车每 8 分发一次车，每次发车的时间一定是 8 的倍数，即第二次发车与第一次发车间隔 8 分，第三次发车与第一次发车间隔 16 分，这样就找到了每次两路电车同时发车的时间，就是求 3 和 8 的最小公倍数。 小红家的客厅长 48 分米，宽 32 分米。现在给客厅的地面铺正方形地砖，有三种砖，你帮小红家想一想，选择哪种地砖能铺得即整齐又不会有余料？ 边长 3 分米 边长 6 分米 边长 8 分米 分析： 求出 48 和 32 的公因数，这个公因数是地砖的边长。 李老师家贮藏室长 16 dm ，宽 12 dm 。如果要用边长是整分米数的正方形地砖把贮藏 室的地面铺满 ( 使用的地砖都是整块 ) 。可以选择边长是几分米的地砖 ? 边长最大是几分米 ? １６和１２的公因数有：１，２，４。最大公因数是４ 答：可以选择边长是 1dm 、 2dm 、 4dm 的地砖 , 边长最大是 4dm 。 男、女生分别排队，男生有 48 人，女生有 36 人。要使每排的人数相同，每排最多有多少人 ? 这时男、女生分别有几排 ? 48 和 36 的最大公因数是 12 。 48÷12 = 4 ( 排 ) 36÷12 = 3 ( 排 ) 答 : 每排最多有 12 人，这时男生有 4 排 , 女生有 3 排。 有一块长方体木块，长 7dm ，宽 5dm ，高 4.5dm 。如果把它锯成同样大小的小正方体木块，最大可以锯成棱长是多少厘米的小方块而又不浪费木料？一共可以锯多少个小正方体木块？ 7dm ＝ 70cm 5dm=50cm 4.5dm=45cm 70 、 50 和 45 的最大公因数是 5 70÷5=14 （个） 50÷5=10 （排） 45÷5=9 （层） 14×10×9=1260 （个） 答 : 最大可以锯成棱长是 5cm 小方块。一共可以锯 1260 个小正方体木块。 一班学生分成 4 人一组或 6 人一组，都正好分完。如果这些学生的总人数在 40 人以内，可能是多少人？ 40 以内 4 和 6 的公倍数有： 12 ， 24 ， 36 。　 答 : 这个班的人数可能是 12 、 24 、 36 人。 甲 5 分钟加工 3 个机器零件，乙 8 分钟加工 5 个同样的零件，比较他们的速度（　　 ）。 ①甲快些 ②乙快些 ③两人一样快 ② 一堆糖果， 3 个 3 个地拿余 1 个， 4 个 4 个地拿余 2 个， 5 个 5 个地拿余 3 个，这堆糖果至少有多少个？ 小数化分数，原来有几位小数就在 1 的后面写几个 0 做分母，把原来的小数去掉小数点作分子； 化成分数后，能约分的要约分。 小数化分数 分数化小数 分母是 10 、 100 、 1000…… 的分数化小数，可以直接去掉分母，看分母中 1 后面有几个零，就在分子中从最后一位起向左数出几位，点上小数点。 分母不是 10 、 100 、 1000… … 的分数化小数，要用分母去除分子；除不尽的，可以根据需要按 四舍五入法 保留几位小数。 一个 最简分数 的分母中只含有质因数 2 和 5 就能化成有限小数。 1 2 1 4 2 5 3 4 1 5 1 8 4 5 3 5 3 8 5 8 7 8 1 20 1 16 3 16 5 16 7 16 1 25 1 50 1 40 把下面的分数化成小数， 并且记住这些结果。 3 2 3 1 20 9 5 8 3 3.025 0.16 0.15 0.2222…… 0.6 3.125 0.375 3 20 0.16 3.025 2 9 3 5 3 1 8 ‹ ‹ ‹ ‹ ‹ ‹ 0.375 把下面各数按从小到大的顺序排列起来。 在（ ）里填上合适的分数 50 厘米 = （ ）米 250 克 = （ ）吨 45 分 = （ ）时 400 米 = （ ）千米 600 毫米 = （ — ）米 40 厘米 = （ — ）米 15 秒 = （ — ）分 2500 平方米 = （ — ）公顷 50 100 1 2 1 4 3 4 2 5 1 1 4 4 3 2 5 5 旋转三要素：旋转点（或旋转中心）、旋转方向、旋转角度 图形的运动（三） 图形的旋转和平移都不改变图形的 大小 和 形状 ，只改变图形的 位置或方向 。 简单图形旋转 90° 的画法 1. 找出图形的关键点或线段。 2. 借助三角板（或量角器）作原图形线段或关键点与旋转中心所在线段的垂线。 3. 在所做垂线上量出与原线段相等的长度（即找出原图关键点的对应点）。 4. 顺次连接所画出的对应点。 （ 1 ）画出图①的全部对称轴。 （ 2 ）画出图②向上平移 3 格后的图形。 图① 图② A O B （ 3 ）画出绕点 O ，顺时针旋转 90 后的图形。 A O B A' A O B A' A O B A' B' A O B A' B' （图一）三角形绕点 O （ ）时针旋转了（ ）度。 （图二）三角形 绕点 O （ ）时针旋转了（ ）度。 逆 90 顺 90 旋转不改变图形的 形状 、 大小 ，只改变图形的 位置 。 图（二） o 图（一） o 分数的加法和减法 分数的加法和减法 分数加减法的简算 异分母分数加减法 同分母分数连减 同分母分数连加 同分母分数加减法 分数加减混合运算 异分母分数连加 异分母分数连减 同分母分数加、减法： 分母不变，只把分子相加减。 异分母分数加、减法： 先 通分， 然后 按照同分母分数加、减法的计算方法进行计算。 分数加减混合运算： 分数加减混合运算的运算顺序和整数加减混合运算的运算顺序相同：没有括号的分数加减混合运算顺序是从左往右依次进行。有括号的分数加减混合运算的运算顺序是先算括号里面的，后算括号外面的。 简便计算： 加法交换律： A+B=B+A 加法结合律： A+B+C=A+(B+C) 减法运算性质： A － B － C=A － (B+C) 2 7 + 3 7 3 8 + 1 8 5 12 - 3 12 4 9 - 2 9 25 36 - 17 36 - 5 36 9 11 - 1. 口算 - 7 11 2 11 注意化简和简算 2. 计算 异分母分数加减法，先通分，转化为同分母分数进行计算。 加法的运算定律和减法的性质同样适应于分数中的计算。 1 2 + 1 3 1 3 + 1 7 1 5 - 1 8 1 9 - 1 16 先计算下面各题，想一想怎样计算比较快？ 用字母表示为： 1 a ± 1 b = b ± a ab a 、 b 均不为 0 1 2 1 4 1 8 1 16 1 32 + + + + 1 32 1 4 1 8 1 16 1 2 1 2 1 4 1 8 1 16 1 32 + + + + 拆项法： 1 2 = 1 - + 1 2 - 1 4 + 1 4 - 1 8 + 1 8 - + 1 16 - 1 32 1 16 = = 1 1 32 - 31 32 解方程 简便计算： 脱式计算： 1 、学校图书馆有故事书占图书总数的 ，工具书占总数的 ，剩下的是科技书，科技书占总数的 几分之几？ 1- - = - - = 答：科技书占总数的 。 2 、小红看一本 100 页的书，第一天看了这本书的 ，第二天看了这本的 ，还剩几分之几没看？ 3 、某乡镇企业，去年上半年完成了全年产值计划的 ，下半年完成了全年产值计划的 。去年这个企业的产值超过了全年产值计划的几分之几？ 在圆圈内填上适当的分数，使每行、每列的三个数加起来的和都等于 1 。 条形统计图 折线统计图 特 点 作 用 折线统计图 用 点 表示数量的多少，用 折线 表示数量的增减幅度和变化趋势。 既能清楚地能看出数量的多少，又能看出数量的增减变化情况。 用直条的长短表 示数量的多少。 从图中能形象直观地看出各数量的多少。 表一 五（ 1 ）班学生爱吃食物人数统计表 食物类别 肉禽类 鱼虾类 蔬菜类 合计 人数 18 20 7 45 表二 光明小学四年级同学喜欢各种玩具的人数统计表 玩具名称 小汽车 洋娃娃 跳棋 拼图 男生人数 22 5 15 18 女生人数 8 24 17 14 表三 光明小学一 ---- 六年级喜欢看科普读物人数统计表 年级 一 二 三 四 五 六 人数 20 26 32 47 68 83 1. 如果将上面的三组数据用统计图的形式表示，你会分别绘制成什么统计图？为什么？ 2. 这些统计图有什么特点？ 表一 五（ 1 ）班学生爱吃食物人数统计表 食物类别 肉禽类 鱼虾类 蔬菜类 合计 人数 18 20 7 45 表二 光明小学四年级同学喜欢各种玩具的人数统计表 玩具名称 小汽车 洋娃娃 跳棋 拼图 男生人数 22 5 15 18 女生人数 8 24 17 14 表一： 单式条形统计图 表二： 复式条形统计图 表三： 单式折线统计图 表三 光明小学一 ---- 六年级喜欢看科普读物人数统计表 年级 一 二 三 四 五 六 人数 20 26 32 47 68 83 例如：关于甲、乙两地月平均气温的 情况用复式折线统计图表示。 复式折线统计图的特点： 便于比较两种数据的变化趋势和差异性。 例如：关于国庆 60 周年与 50 周年 阅兵式方阵数量统计图。 复式条形统计图的特点： 便于比较不同组之间的同类数据。 运用知识解决问题 1. 选择 （ 1 ）心脏科要把病人的血压变化情况绘制成统计图，最佳选择是（ ） A 条形统计图 B 折线统计图 （ 2 ）要表示某校各班向灾区捐款情况，选用（ ）比较合适。 A 条形统计图 B 折线统计图 （ 1 ）如果你是世界环保组织成员，想呼吁大家关注碳排 放量，让大家强烈地感受到一定要降低碳排放量， 你将选择 （ ） 统计图来表达。 理由是： 折线 突出空气中碳的排放量越来越高的发展趋势。 2 n -1 到第 n 分钟所有接到通知的队员总数 第几分钟 接到通知的队员总数就等于 几个 2 相乘再减 1 打电话 找次品 2-3 4-9 10-27 28-81 82-243 1 次 2 次 3 次 4 次 5 次