五年级上册数学课件-第六单元整理和复习 人教版(共24张PPT)

五年级上册数学课件-第六单元整理和复习 人教版(共24张PPT)

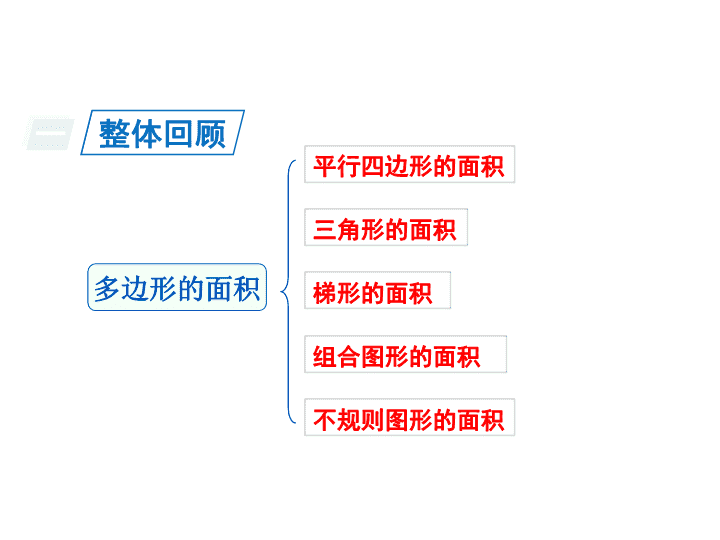
多边形的面积 6 人教版五年级数学上册 整理和复习 一 整体回顾 多边形的面积 平行四边形的面积 三角形的面积 梯形的面积 组合图形的面积 不规则图形的面积 二 知识梳理 平行四边形的面积 S = ah 平行四边形面 积 底 高 × = 平行四边形面积公式的应用 在平行四边形中，只要知道底、高和面积三个量中的任意两个量，就可以根据平行四边形的面积计算公式求出第三个量。 平行四边形的面积 有一块平行四边形菜地，底 是 24 0 m ，高 是 12 5 m ，在这块地里共收油菜 籽 7.3 8 吨 。这块菜地有多少公顷？平均每公顷菜地收油菜籽多少吨？ S 菜 地 = 240 ×12 5 = 3000 0( m 2 ) 3000 0 m 2 = 3 公顷 平均每公顷菜地收油菜籽： 7.38 ÷ 3 = 2.46 （吨） 答： 这块菜地 有 3 公顷，平均每公顷收油菜 籽 2.4 6 吨。 三角形的面积 三角形的面 积 底 高 × = 三角形面积公式的应用 在三角形中，只要知道三角形的底、高和面积这三个量中的任意两个量，就可以根据三角形的面积计算公式求出第三个量。 ÷ 2 S = ah ÷ 2 三角形的面积 在一个长方形花坛里划一块三角形地种蔬菜（如图）。如果在三角形地里平均每平方米 种 2 5 棵蔬菜，那么这块三角形地一共可以种多少棵蔬菜？ S 菜 地 = 16 ×8÷ 2 = 6 4( m 2 ) 三角形可以种的蔬菜： 25 ×6 4 = 1600 （棵） 答： 这块三角形地一共可以 种 160 0 棵蔬菜。 1 6 m 8 m 种蔬菜 （ 上底 + 下底 ） 梯形的面积 梯形的面 积 高 × = 梯形面积公式的应用 如果知道梯形的面积、上底、下底和高这四个量中的任意三个量，就可以根据梯形的面积计算公式求出第四个量。 ÷ 2 S= ( a +b ) h ÷ 2 梯形的面积 如图，一个梯形的上、下底分别 是 6 cm 、 1 0 cm ， 已知阴影部分的面积 是 2 4 cm 2 ，这个梯形的面积是多少平方厘米。 24 ×2÷1 0 = 4. 8( c m ) 三角形的高是： 答： 这个梯形的面积 是 38. 4 cm 2 。 1 0 cm 6 cm S 梯 形 = (6+ 1 0 ) × 4.8 ÷ 2 = 38. 4( cm 2 ) 在实际生活中，有些图形是由几个简单的图形组合而成的。在计算组合图形的面积时，通常有两种方法： 分割求和法 和 添补求差法 。 分割求和法 先把图形分解成几个学习过的简单图形，分别计算出各个简单图形的面积，然后加起来，即可求出整个图形的面积。 组合图形的面积 在实际生活中，有些图形是由几个简单的图形组合而成的。在计算组合图形的面积时，通常有两种方法： 分割求和法 和 添补求差法 。 添补求差法 有些组合图形时从已学过的简单图形中减去一个（或几个）已学过的简单图形而构成，需要从一个图形面积中减去另一个（或几个）图形的面积。 组合图形的面积 计算下面图形的面积。你能想出几种方法？ ( 教科书第 103 页整理和复习 2) 添补求差法 方法一：长方形减梯形 S 长方 形 = 12 × 1 0= 12 0( cm 2 ) S 梯 形 = (6+ 1 2 ) × ( 1 0−5 ) ÷ 2 = 45 ( cm 2 ) S= 12 0− 4 5 = 7 5( cm 2 ) 分割求和法 方法二：长方形加梯形 S 长方 形 = 6 × 5= 3 0( cm 2 ) S 梯 形 = (5+ 1 0 ) × ( 1 2−6 ) ÷ 2 = 4 5( cm 2 ) S= 3 0+ 4 5 = 7 5( cm 2 ) 分割求和法 方法三：三角形加梯形 S 三角 形 = 10 × ( 1 2−6 ) ÷2 = 3 0( cm 2 ) S 梯 形 = (6+ 1 2 ) × 5 ÷ 2 = 4 5( cm 2 ) S= 3 0+ 4 5 = 7 5( cm 2 ) 分割求和法 方法四：三角形加长方形 S 三角 形 = ( 1 0−5 ) × ( 1 2−6 ) ÷ 2 = 1 5 (cm 2 ) S 长方 形 = 1 2 × 5= 6 0( cm 2 ) S= 1 5+ 6 0= 7 5( cm 2 ) 分割求和法 方法五：三角形加三角形 S 大三角 形 = 1 0 × 1 2 ÷ 2 = 6 0 (cm 2 ) S 小三角 形 = 6 × 5 ÷ 2 = 1 5( cm 2 ) S= 6 0+ 1 5= 7 5( cm 2 ) 不规则图形的面积估算 估算不规则图形的面积，可以通过数方格方法确定出不规则图形面积的范围，再估算出其面积的大小；也可以将不规则图形的面积转化为与它形状相近的已学过的图形来估算。 不规则图形的面积 小练笔 回忆下图形面积计算公式的推导过程，写出计算公式。 （教科书第 103 页整理和复习 1 ） ɑ b S= ɑb ɑ h S= ɑh ɑ h S= ɑh S = ah ÷ 2 S= ( a +b ) h ÷ 2 ɑ h ɑ b h 平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。 ɑ b h 当梯形的上底和下底相等时就成了平行四边形；当梯形的上底 为 0 时就成了三角形。 ɑ h ɑ h 这个由一副七巧板拼出的正方形边长 为 1 2 cm ，你能求出每个图形的面积吗？ （教科书第 103 页整理和复习思考题） ① ② ③ ④ ⑤ ⑥ ⑦ 图形①、⑤： 12 × ( 1 2 ÷ 2 )÷ 2 = 3 6 (cm 2 ) 图形②： ( 1 2 ÷ 2 )× ( 1 2 ÷ 4 ) = 1 8 (cm 2 ) 图形③： ( 1 2 ÷ 2 )× ( 1 2 ÷ 2 )÷ 2 = 1 8 (cm 2 ) 这个由一副七巧板拼出的正方形边长 为 1 2 cm ，你能求出每个图形的面积吗？ （教科书第 103 页整理和复习思考题） ① ② ③ ④ ⑤ ⑥ ⑦ 图形④、⑥： ( 1 2 ÷ 2) × ( 1 2 ÷ 4 )÷ 2 = 9 (cm 2 ) 图形⑦： ( 1 2 ÷ 2) × ( 1 2 ÷ 4 ) = 1 8 (cm 2 ) 三 随堂练习 1. 下图中阴影部分的面积 是 1 5 cm 2 ，三角形 ABC 的面积是多少平方厘米？ A B C 3 cm 5 cm 15 ×2÷ 3 = 1 0( c m ) 三角形的高是： 答： 三角形 ABC 的面积 是 4 0 cm 2 。 S ABC = (3+5 ) × 10 ÷ 2 = 4 0( cm 2 ) 2. 在国庆节期间，市中心广场东面布置了一个大型的梯形花卉盆景，它的上底 是 2 1 m ，下底 是 3 5 m ，整个盆景占地面积 是 33 6 m 2 。 这个梯形的高是多少米？ 336 ×2÷ ( 2 1+ 3 5 )= 1 2( m ) 答： 这个梯形的高 是 1 2 m 。 课后作业 1. 从课后习题中选取； 2. 完成练习册本课时的习题。