四年级上册数学单元测试-2.几何小天地

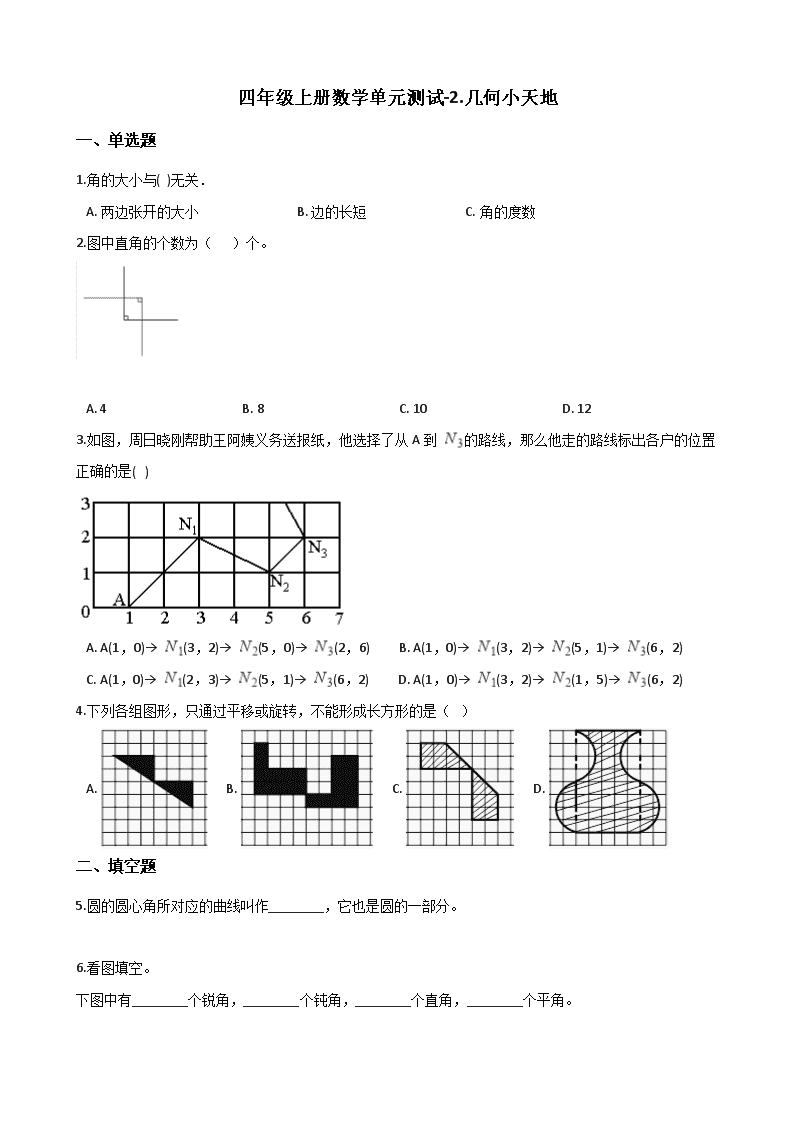
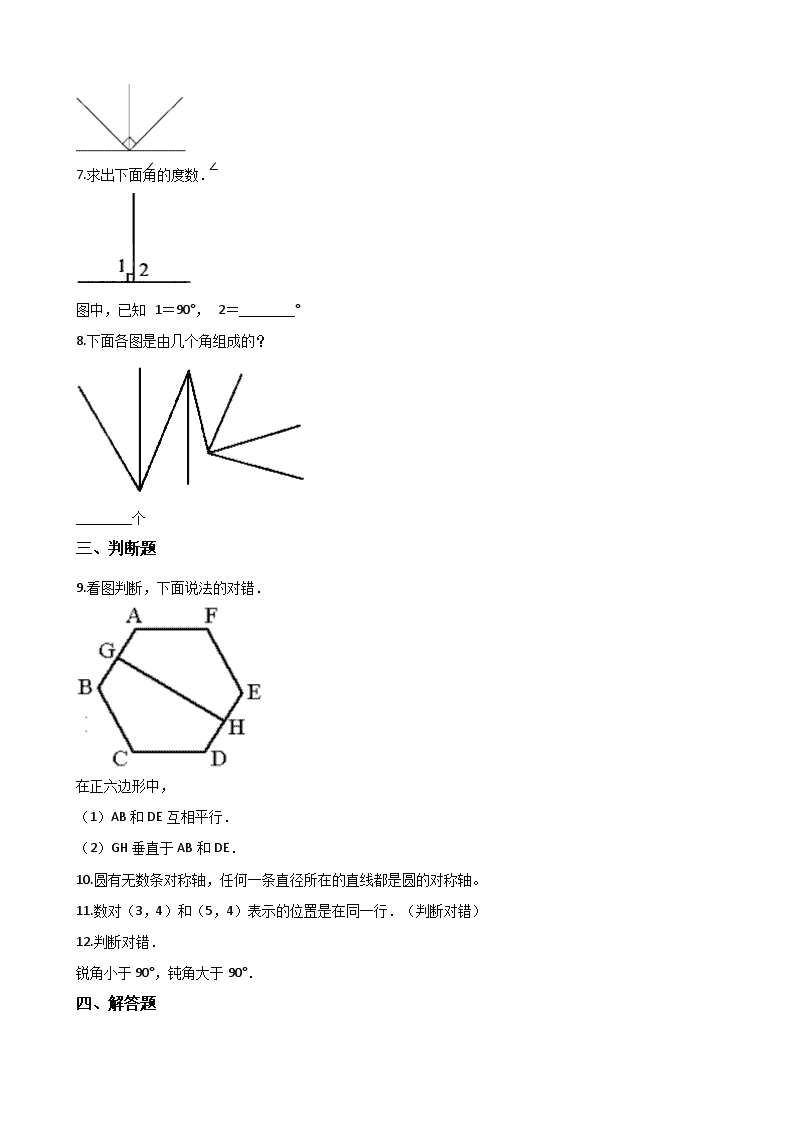
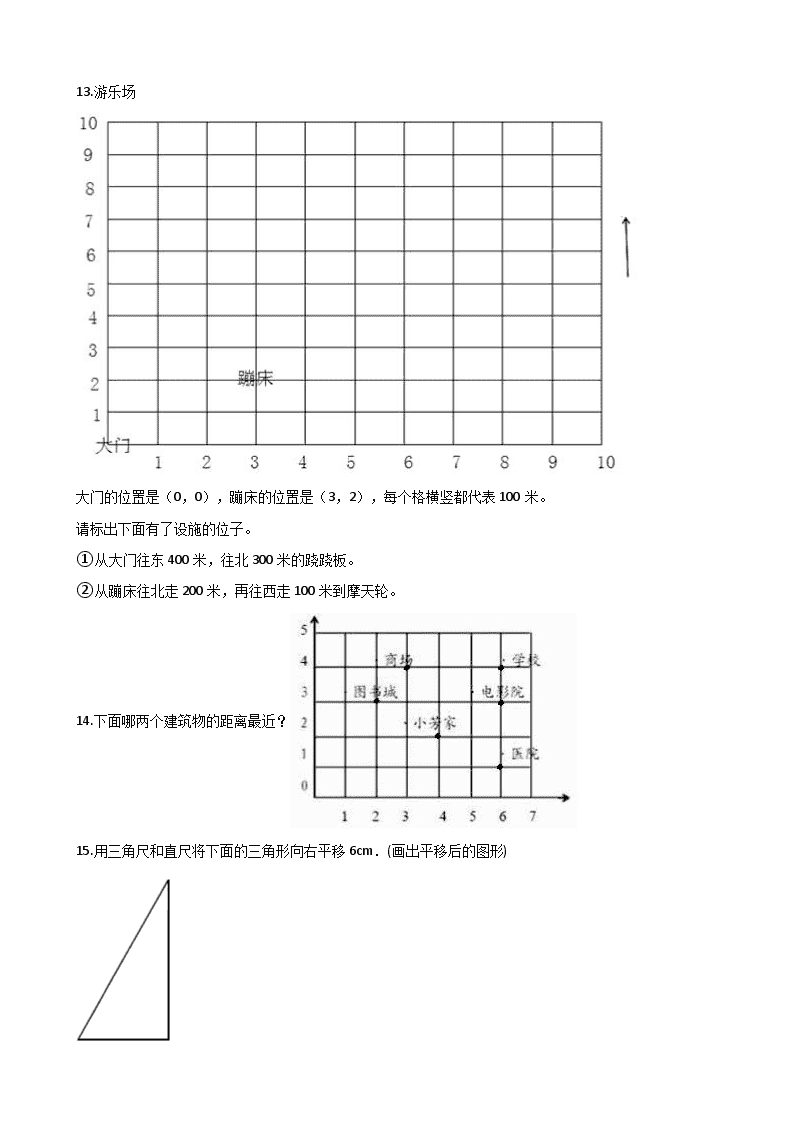
四年级上册数学单元测试-2.几何小天地

‎ ‎ 四年级上册数学单元测试-2.几何小天地 ‎ 一、单选题 ‎ ‎1.角的大小与(  )无关． ‎ A. 两边张开的大小                               B. 边的长短                               C. 角的度数 ‎2.图中直角的个数为（     ）个。 ‎ A. 4                                          B. 8                                          C. 10                                          D. 12‎ ‎3.如图，周日晓刚帮助王阿姨义务送报纸，他选择了从A到 的路线，那么他走的路线标出各户的位置正确的是(   )‎ A. A(1，0)→ (3，2)→ (5，0)→ (2，6)         B. A(1，0)→ (3，2)→ (5，1)→ (6，2) C. A(1，0)→ (2，3)→ (5，1)→ (6，2)         D. A(1，0)→ (3，2)→ (1，5)→ (6，2)‎ ‎4.下列各组图形，只通过平移或旋转，不能形成长方形的是（  ） ‎ A.       B.       C.       D. ‎ 二、填空题 ‎ ‎5.圆的圆心角所对应的曲线叫作________，它也是圆的一部分。 ‎ ‎6.看图填空。‎ 下图中有________个锐角，________个钝角，________个直角，________个平角。‎ ‎ ‎ ‎ ‎ ‎7.求出下面角的度数． 图中，已知∠1＝90°，∠2＝________° ‎ ‎8.下面各图是由几个角组成的？ ________个 ‎ 三、判断题 ‎ ‎9.看图判断，下面说法的对错．‎ 在正六边形中，‎ ‎（1）AB和DE互相平行． ‎ ‎（2）GH垂直于AB和DE． ‎ ‎10.圆有无数条对称轴，任何一条直径所在的直线都是圆的对称轴。 ‎ ‎11.数对（3，4）和（5，4）表示的位置是在同一行．（判断对错） ‎ ‎12.判断对错． 锐角小于90°，钝角大于90°． ‎ 四、解答题 ‎ ‎ ‎ ‎ ‎ ‎13.游乐场 大门的位置是（0，0），蹦床的位置是（3，2），每个格横竖都代表100米。 请标出下面有了设施的位子。 ①从大门往东400米，往北300米的跷跷板。 ②从蹦床往北走200米，再往西走100米到摩天轮。 ‎ ‎14.下面哪两个建筑物的距离最近？‎ ‎15.用三角尺和直尺将下面的三角形向右平移6cm．(画出平移后的图形)‎ ‎ ‎ ‎ ‎ 五、综合题 ‎ ‎16.看图填空 ‎ ‎（1）图书馆的位置在第________列，第________行，表示为（________，________） ‎ ‎（2）学校在图中的位置是（________，________）；小天家的位置是（________，________） ‎ ‎（3）（3，3）这点在图上是________的位置． ‎ ‎（4）（9，2）这点在图上是________位置． ‎ 六、应用题 ‎ ‎17.①作出如图三角形底边上的高． ②过A点作底边的平行线． ③量出计算三角形面积所需的数据并标在图上（取整毫米）． ④计算出三角形的面积． ‎ ‎ ‎ ‎ ‎ 参考答案 一、单选题 ‎1.【答案】B ‎ ‎【解析】【解答】角的大小与边的长短无关. 故答案为：B.‎ ‎【分析】根据对角的认识可知，角的大小与边的长短无关，与两边张开的大小有关，据此解答.‎ ‎2.【答案】C ‎ ‎【解析】【解答】解：两个直角边的交叉点处公有8个直角，再加上2个，共10个直角. 故答案为：C ‎【分析】直角是90°的角，除了标出的两个直角外，两条直角边相交成的4个角也是直角.‎ ‎3.【答案】 B ‎ ‎【解析】【解答】周日晓刚帮助王阿姨义务送报纸，他选择了从A到N3的路线，那么他走的路线标出各户的位置正确的是：A(1，0)→ N1(3，2)→ N2(5，1)→ N3(6，2). 故答案为：B.‎ ‎【分析】用数对表示位置时，通常用两个数字表示，第一个数字表示第几列，第二个数字表示第几行，据此解答.‎ ‎4.【答案】C ‎ ‎【解析】【解答】选C。【分析】A可以绕两个三角形的交点顺时针旋转180度，B先向上平移一格，再绕两个图形的相交点逆时针旋转90度，D可以把右下的图形先向上平移4格，再向左平移5格，左下的图形先向上平移4格，再向右平移5格就得到了长方形。‎ 二、填空题 ‎5.【答案】弧 ‎ ‎【解析】【解答】圆的圆心角所对应的曲线叫作弧，它也是圆的一部分. 故答案为：弧.‎ ‎【分析】一条圆弧和经过这条圆弧两端的两条半径所围成的图形叫扇形，圆的圆心角所对应的曲线叫作弧，它也是圆的一部分.‎ ‎6.【答案】4；2；3；1 ‎ ‎ ‎ ‎ ‎ ‎【解析】【解答】观察图形可知，图中有4个锐角，2个钝角，3个直角，1个平角. 故答案为：4；2；3；1.‎ ‎【分析】角的分类：0°＜锐角＜90°，直角=90°，90°＜钝角＜180°，平角=180°，周角=360°，据此解答.‎ ‎7.【答案】90 ‎ ‎【解析】【解答】解：∠2=180°-90°=90° 故答案为：90 【分析】∠1和∠2组成平角，平角是180°的角，因此用180°减去90°即可求出∠2的度数.‎ ‎8.【答案】12 ‎ ‎【解析】【解答】解：单独的角7个，由两个角组成的角4个，由三个角组成的角1个，共7+4+1=12(个) 故答案为：12 【分析】先数出单独的角，然后分别数出由两个角组成的角和三个角组成的角即可判断角的个数.‎ 三、判断题 ‎9.【答案】（1）1 （2）1 ‎ ‎【解析】【解答】(1)AB和DE是永不相交的两条线段，是互相平行的；原题说法正确； (2)GH和AB与DE相交都成直角，是互相垂直的；原题说法正确. 故答案为：正确；正确 ‎【分析】在同一平面内，永不相交的两条直线互相平行；相交成直角的两条直线互相垂直；由此根据平行与垂直的定义判断即可.‎ ‎10.【答案】 正确 ‎ ‎【解析】【解答】圆有无数条对称轴，任何一条直径所在的直线都是圆的对称轴。 ‎ ‎【分析】根据圆的特征、轴对称图形的特征，注意，语言要严密，不能说成圆的直径就是圆的对称轴，因为对称轴是一条直线，直径是线段。‎ ‎11.【答案】正确 ‎ ‎【解析】【解答】解：（3，4）表示第3列第4行，（5，4）表示第5列第4行，它们都表示第4行； 原题说法正确． 故答案为：正确． 【分析】数对表示位置时，第一个数表示列数，第二个数表示行数；所以（3，4）表示第3列第4行，（5，4）表示第5列第4行，据此做出判断．‎ ‎12.【答案】错误 ‎ ‎ ‎ ‎ ‎ ‎【解析】【解答】解：钝角大于90°而小于180°，原题说法错误. 故答案为：错误 【分析】直角是90度，平角是180度，周角是360度，锐角小于90度，钝角大于90度小于180度.‎ 四、解答题 ‎13.【答案】解： ‎ ‎【解析】【分析】题目中，每个格横竖都代表100米，先用总米数除以100，然后再标位置，根据方位图，可以知道，向东走就是将位置向右移动，向西走就是将位置向左移动，向北走就是将位置向上移动，向南走就是将位置向下移动。‎ ‎14.【答案】解：学校和电影院。 ‎ ‎【解析】【分析】图书城的位置是（2，3），商场的位置是（3，4），小芳家的位置是（4，2），医院的位置是（6，1），电影院的位置是（6，3），学校的位置是（6，4），根据各个建筑物的位置，医院、电影院、学校处于同一列，学校和电影院只相差一行，所以学校和电影院的距离最近。‎ ‎15.【答案】 解：画图如下：‎ ‎ ‎ ‎ ‎ ‎【解析】【分析】用直尺的0刻度对准左图的一个点，直尺水平放置，然后在6厘米处点上对应的点，按照这样的方法点出三个对应的点并连线成三角形即可.‎ 五、综合题 ‎16.【答案】 （1）3；6；3；6 （2）7；4；5；2 （3）邮局 （4）超市 ‎ ‎【解析】【解答】解：（1）图书馆的位置在第3列，第6行，表示为（3，6）（2）学校在图中的位置是（7，4）；小天家的位置是（5，2）（3）（3，3）这点在图上是邮局的位置．（4）（9，2）这点在图上是超市位置． ‎ 故答案为：3，6，6，6；7，4，5，2；邮局，超市．‎ ‎【分析】（1）图书馆所在的列、与行由图即可看出，根据用数对表示点的位置的方法，第一个数字表示列数，第二个数字表示行数，即可用数对表示图书馆的位置．（2）同理，即可用数对表示出学校、小天家的位置．（3）根据数对（3，3），即第3列，第3行，即可确定该点表示的设施名称．（4）同理，根据数对（9，2），即第3列，第3行，即可确定该点表示的设施名称．‎ 六、应用题 ‎17.【答案】解：根据题干分析，画图如下： 经过测量可知三角形的底是2.5厘米，高是2厘米，所以面积是： 2.5×2÷2=2.5（平方厘米）； 答：这个三角形的面积是2.5平方厘米 ‎ ‎【解析】【分析】①在三角形中，从一个顶点向它的对边所在的直线作垂线，顶点到垂足之间的线段叫做三角形的高，由此进行作图即可；②用直角三角尺的一条直角边与底边重合，直尺边与直角三角形的另一边重合，再移动三角板直到与顶点A重合，沿直角边划一直线即可；③三角形的面积=底×高÷2，所以只要测量出这个三角形点的底和高即可；④利用三角形的面积公式，代入测量出的数据即可解答．此题主要是考查过直线外一点作直线的平行线和垂线的方法以及三角形的面积公式的灵活应用．‎ ‎ ‎