四年级数学《智慧广场——植树问题》

四年级数学《智慧广场——植树问题》

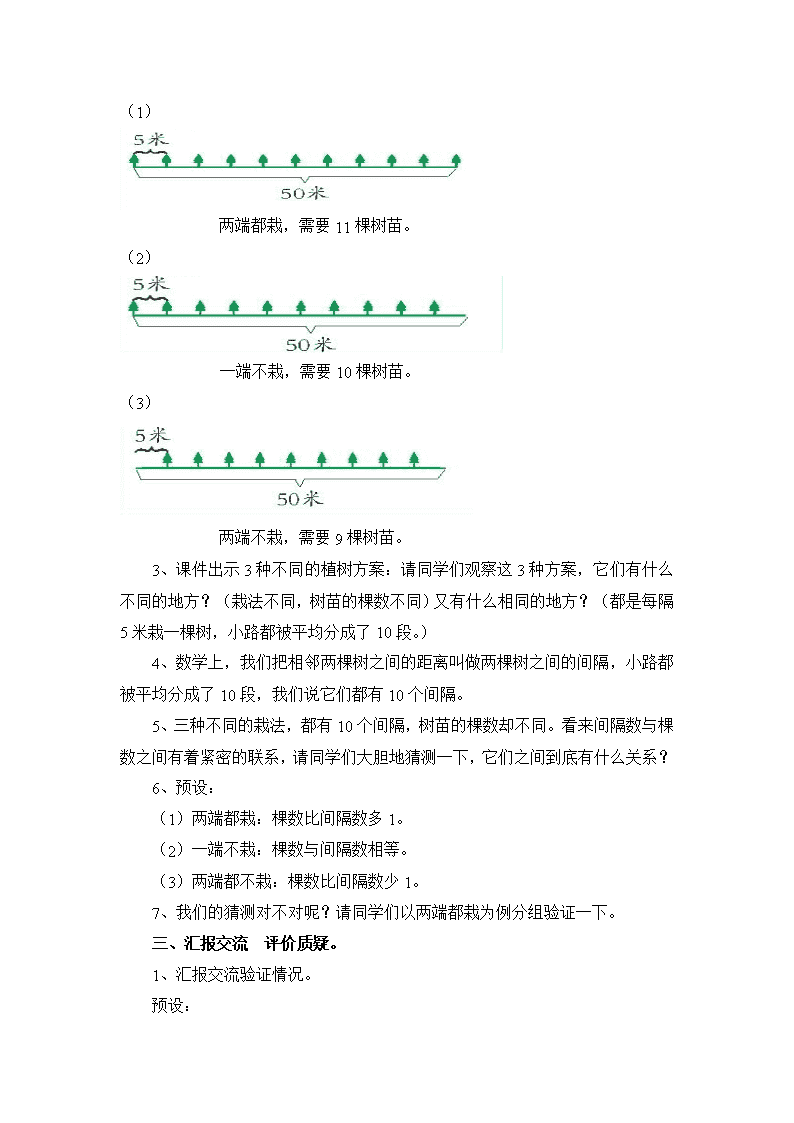
智慧广场——植树问题 教学内容： 小学数学四年级上册第106-107页智慧广场。‎ 教学目标：‎ ‎1．结合植树的情境，借助生活经验和画图的策略学习并掌握间隔现象中的规律。‎ ‎2．在丰富的素材中，经历观察、操作、分析等寻找规律的过程，逐步从感性认识上升到理性认识，掌握探究的方法，提高思维能力。‎ ‎3．在充分的自主探索、合作交流中，增强探究的欲望，体验成功的喜悦，感受数学的魅力。‎ 教学重难点：‎ 教学重点：探究“两端都栽、一端不栽、两端都不栽”的植树棵数与间隔之间的关系，发现在一条直线上植树问题的规律，经历数学建模的过程。‎ 教学难点：灵活运用植树问题的规律解决生活中的各种实际问题。‎ 教具、学具：‎ 教师准备：课件、《学习情况自我评价表》。‎ 学生准备：学习纸 。‎ 教学过程：‎ 一、创设情境，提出问题 ‎1、出示教材106页智慧广场情境图：‎ ‎（1）从图中你知道了哪些数学信息？‎ ‎ 预设：（50米的小路； 一旁植树；每5米载一棵。）‎ ‎（2）根据这些信息，你能提出什么问题？‎ ‎ 预设：如果两端都栽，需要多少棵树苗？‎ ‎ 如果一端不栽，需要多少棵树苗？‎ ‎ 如果两端不栽，需要多少棵树苗？‎ 二、 自主学习，合作探究 ‎ 1、 请各小组把你们的植树方案画下来，看看你们的植树方案需要多少棵树苗？（学生画图，教师巡视。）‎ ‎ 2、汇报交流。‎ 预设：‎ ‎（1）‎ ‎ 两端都栽，需要11棵树苗。‎ ‎（2）‎ ‎ 一端不栽，需要10棵树苗。‎ ‎（3）‎ ‎ 两端不栽，需要9棵树苗。‎ ‎3、课件出示3种不同的植树方案：请同学们观察这3种方案，它们有什么不同的地方？（栽法不同，树苗的棵数不同）又有什么相同的地方？（都是每隔5米栽一棵树，小路都被平均分成了10段。）‎ ‎4、数学上，我们把相邻两棵树之间的距离叫做两棵树之间的间隔，小路都被平均分成了10段，我们说它们都有10个间隔。‎ ‎5、三种不同的栽法，都有10个间隔，树苗的棵数却不同。看来间隔数与棵数之间有着紧密的联系，请同学们大胆地猜测一下，它们之间到底有什么关系？‎ ‎6、预设：‎ （1） 两端都栽：棵数比间隔数多1。‎ （2） 一端不栽：棵数与间隔数相等。‎ （3） 两端都不栽：棵数比间隔数少1。‎ ‎ 7、我们的猜测对不对呢？请同学们以两端都栽为例分组验证一下。 ‎ 三、汇报交流 评价质疑。‎ ‎1、汇报交流验证情况。‎ 预设： ‎ （1） ‎ 1 2 3 4 5 6 7 8 9 10 ‎ ‎ 1 2 3 4 5 6 7 8 9 10 11‎ ‎ 我们一棵树一个间隔这样一对一对的数，发现棵数比间隔数多1。‎ ‎（2） ‎ ‎ ‎ ‎ ‎ ‎ 我们发现：有一个间隔可以栽2棵树，2个间隔可以栽3棵树，3个间隔可以栽4棵树······棵数总是比间隔数多1。‎ ‎（3）我们用手指代表树，5个手指表示5棵小树，有4个“间隔”，棵数比间隔数多1。‎ ‎2、你能用一个式子表示两端都栽的情况下间隔数与棵数之间的关系吗？‎ ‎ （间隔数＋1=棵数）‎ ‎3、现在你能列出算式计算两端都栽，需要多少棵树苗吗？‎ ‎ 50÷5+1=11（棵）答：两端都栽，需要11棵树苗。‎ ‎ 间隔数 ‎4、你能应用规律解决问题吗：在一条全长180米的街道一旁安装路灯，（两端都要安装），每隔6米安一座。一共要安装多少座路灯？‎ ‎5、你能独立验证一端不栽和两端不栽的情况下，间隔数和棵数之间的关系吗？‎ （1） 学生独立验证。‎ （2） 汇报交流。‎ ①一端不栽：‎ ‎ 有10个间隔，栽10棵树。间隔数=棵数。‎ 握住大拇指，还剩4个手指，表示4棵小树，有4个“间隔”，间隔数=棵数。‎ 算式：50÷5=10（棵）答：一端不栽，需要10棵树苗。‎ ②两端不栽：‎ 有10个间隔，栽9棵树。间隔数-1=棵数。‎ 握住大拇指和小拇指，还剩3个手指，表示3棵小树，有4个“间隔”，间隔数—1=棵数。‎ 算式：50÷5-1=9（棵）答：两端不栽，需要9棵树苗。‎ ‎ 间隔数 四、抽象概括 ，总结提升。‎ ‎1、请同学们小组合作总结三种情况下，间隔数与棵数之间的关系？‎ （1） 学生分组活动，教师巡视。‎ （2） 汇报交流。‎ ‎ 两端都栽：‎ ‎ ‎ ‎ 间隔数+1=棵数 ‎ ‎ 一端不栽：‎ ‎ ‎ 间隔数=棵数 ‎ 两端不栽：‎ ‎ ‎ 间隔数-1=棵数 ‎2、学法小结：画图或是借助“手”来研究等方法都是我们解决数学问题的好方法，在以后的生活和学习过程中，我们要学会灵活运用。‎ 五、拓展应用 ，巩固提高。‎ ‎1、一条走廊长32米，每隔4米放一盆花，两端都要放，一共需要放多少盆花？（先画出示意图，再列式解答）‎ ‎2、把一根木头锯成5段，每锯段一次需要6分钟，锯完这根木头一共需要多少分钟？（先画出示意图，再列式解答）‎ 探究提示：“段数”相当于什么？“锯的次数”相当于什么？‎ ‎ 学法小结：锯木头其实就是两端不栽的植树问题。‎ ‎3、为了保护一棵古树，园林处要为它做一个30米长的圆形防护栏。如果每隔两米打一个桩，一共需要打多少个桩？‎ 探究提示：‎ （1） 画出示意图。‎ （2） 把你画的圆形示意图在一个木桩处截开，画成直线认真观察一下！‎ （3） ‎“木桩个数”相当于什么？‎ ‎ ‎ ‎ ‎ 学法小结：做圆形护栏其实就是一端不栽的植树问题。‎ 每5米装一盏灯，你知道桥的两边各装了多少盏灯吗？‎ ‎4、 ‎ ‎ ‎ ‎ 拓展：你知道两边一共装多少盏灯吗？‎ ‎5、公园小路一侧有一排椅子，从起点到终点一共有50把椅子，每两把椅子之间相距8米。这条小路长多少米？‎ 探究提示：‎ ‎（1）椅子相当于什么？‎ ‎（2）从起点到终点一共有50把椅子，说明了什么？‎ ‎（3）50把椅子把这条小路分成了多少个间隔？‎ 6、 评价反思：这节课你有什么收获？请同学们利用《学习情况自我评价表》对自己的学习情况进行评价。（后附《学习情况自我评价表》）‎ 板书设计：‎ ‎ 智慧广场——植树问题 ‎ ‎ ‎ 两端都栽：间隔数 + 1 = 棵数 ‎ 50÷5+1=11（棵）‎ ‎ 间隔数 ‎ 答：两端都栽，需要11棵树苗。‎ ‎ 一端不栽：间隔数 = 棵数 ‎ 50÷5=10（棵）‎ ‎ 答：一端不栽，需要10棵树苗。‎ ‎ 两端不栽：间隔数 -1 = 棵数 ‎ 50÷5-1=9（棵）‎ ‎ 间隔数 ‎ 答：两端不栽，需要9棵树苗。‎ ‎ 设计说明：‎ （1） 充分挖掘学生生活经验，促进学生自主探究。创设源于现实生活的植树情境，借助学生的生活经验，引导学生提出两端都栽，一端不载，两端都不栽分别需要多少树苗的问题，从而引出对三种情况存在的不同规律的探究。在探究规律时，学生借助画图和手，经历观察、操作、分析等过程从而发现了规律。这样通过对学生已有生活经验的利用，有利于学生对间隔现象规律的自主探究以及理解和掌握。‎ （2） 注重让学生经历探究的过程，发现并理解规律。教学时我让学生用画图和手指的方法表示自己的想法。在交流的过程中通过展示让学生直观感受到不同情况下植树的棵数和间隔数的关系，在这个基础上，再借助示意图采用树与间隔一一对应的方法发现规律，并理解为什么会存在这样的规律。‎ （3） 寻找实际问题中的本质联系，促进方法的迁移。如在解决“锯完这块木头一共需要几分钟”这个问题时，我引导学生分析“段数”就相当于“间隔数”，“锯的次数”就相当于“棵数”，“锯木头”实际上就是“两端都不栽”的情况，从而让学生自主迁移规律解决问题。又如，在解决“一共需要打多少个桩？”这个问题时，我引导学生把“在封闭曲线上植树”转化成在直线上“只栽一端”的情况，从而使问题迎刃而解.‎ 评价目标 评价内容 ‎ 评价结果 知 识 技 能 我知道了两端都栽时：间隔数+1=棵数 我知道了一端不栽时：间隔数=棵数 我知道了两端不栽时：间隔数-1=棵数 我会用画图的方法探究植树问题的规律。‎ 我会利用手指探究植树问题的规律。‎ 数 学 思 考 我能把“锯木头”的问题转化成两端不栽的植树问题。‎ 我能把“做圆形护栏”的问题转化成一端不栽的植树问题。‎ 问 题 解 决 我能利用植树问题的规律解决生活中的摆花、装路灯、安护栏等实际问题。‎ 情 感 态 度 我愿意了解生活中与数学相关的信息。‎ 我能在与同学的交流中完善自己的想法。‎ 我认识到数学知识和方法很有价值。‎ 我乐于思考，勇于质疑。‎