- 2021-11-24 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
三年级数学下册教案《 简单的时间计算》
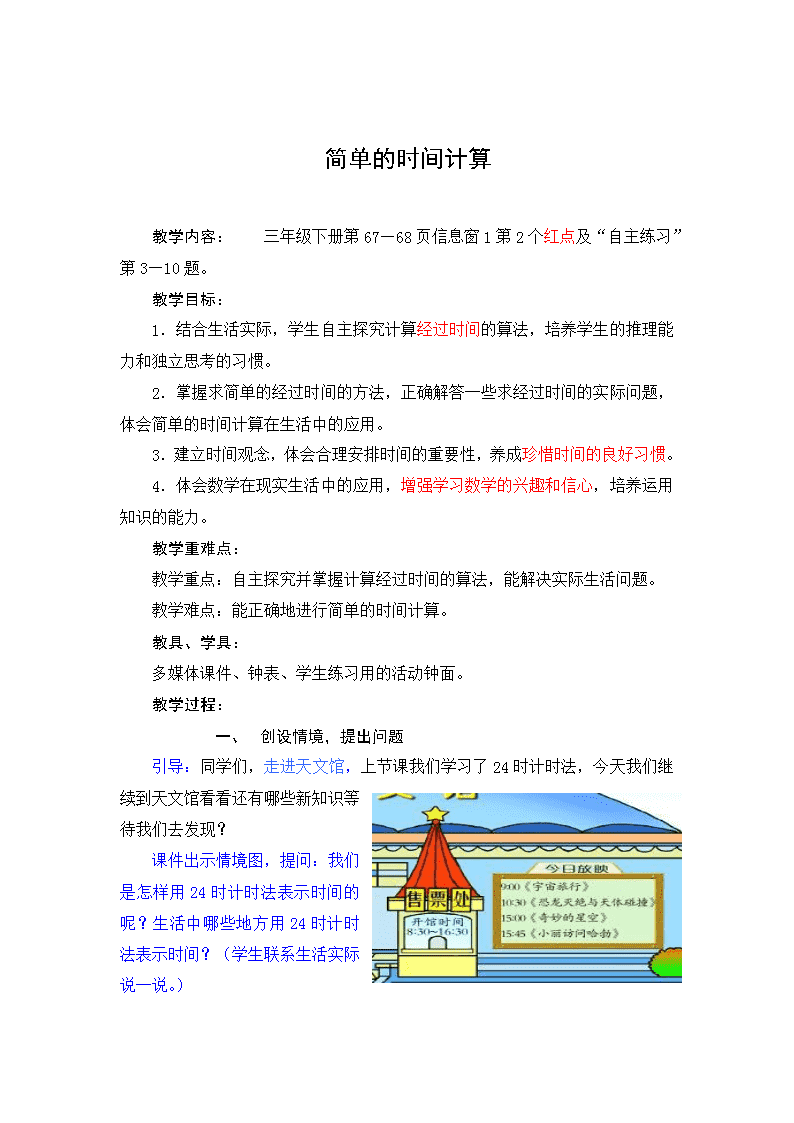
简单的时间计算 教学内容: 三年级下册第67—68页信息窗1第2个红点及“自主练习”第3—10题。 教学目标: 1. 结合生活实际,学生自主探究计算经过时间的算法,培养学生的推理能力和独立思考的习惯。 2. 掌握求简单的经过时间的方法,正确解答一些求经过时间的实际问题,体会简单的时间计算在生活中的应用。 3. 建立时间观念,体会合理安排时间的重要性,养成珍惜时间的良好习惯。 4. 体会数学在现实生活中的应用,增强学习数学的兴趣和信心,培养运用知识的能力。 教学重难点: 教学重点:自主探究并掌握计算经过时间的算法,能解决实际生活问题。 教学难点:能正确地进行简单的时间计算。 教具、学具: 多媒体课件、钟表、学生练习用的活动钟面。 教学过程: 一、 创设情境,提出问题 引导:同学们,走进天文馆,上节课我们学习了24时计时法,今天我们继续到天文馆看看还有哪些新知识等待我们去发现? 课件出示情境图,提问:我们是怎样用24时计时法表示时间的呢?生活中哪些地方用24时计时法表示时间?(学生联系生活实际说一说。) 让学生仔细观察画面,找出数学信息。 预设1:天文馆的开馆时间是8:30~16:30 预设2:科教片今日放映的片名和安排是: 《宇宙旅行》 9:00 《恐龙灭绝与天体碰撞》 10:30 《奇妙的星空》 15:00 《小丽访问哈勃》 15:45 引导:根据这些信息,你能提出哪些数学问题?(教师有选择的将问题板书在黑板上) 学生可能提出的问题预设: 问题1:天文馆每天开馆多长时间? 问题2:从《恐龙灭绝与天体碰撞》开映到《奇妙的星空》开映间隔时间有多长? 问题3:《小丽访问哈勃》播放了多长时间? …… 引导:大家可真了不起,提出了这么多的问题,针对同学们提出的问题,这节课我们一起来研究简单的时间计算(板书课题)! 【设计意图:由信息窗情境图导入,引导学生观察、提出有关时间的问题,不仅培养了学生的问题意识,同时也培养学生用数学的眼光观察生活的能力,让学生体会身边的数学。】 一、 自主学习,小组探究 引导:现在让我们一起去解决问题吧,下面请大家尝试解决:开馆时间8:30--16:30,天文馆一天的开馆时间有多长? 为了更好的进行研究,老师给同学们一点小小提示:(课件出示) 【温馨提示】 1.找一找:天文馆什么时间开门,什么时间结束? 2.利用你手中的材料,大胆地拨一拨、画一画、数一数,想办法算一算。 师:现在大家开始研究问题,如果遇到困难,可以请老师帮忙。 附:小组研究记录 研究的问题 我们的发现 学生根据探究提示尝试解决,教师巡视指导,及时了解学生的学习情况 【设计意图:对学生进行大胆地放手,让学生自己经历探究经过时间的过程,温馨提示也仅是简单的对学生进行引导运用探究材料,教师不能代其劳,学生才能通过不同的方法,探索怎样求经过时间,感受探究的乐趣,提高解决问题的的能力和锻炼思维能力。】 三、汇报交流,质疑评价 解决问题:天文馆每天开馆多长时间? 引导:老师发现大家刚才研究的都非常的认真!哪个小组愿意将你们小组的想法与大家一起分享一下? 【学习目的】学习不借位计算,理解单位的写法。 1.学习不借位减 预设1:数一数,我是数的,从8:30开始数,9:30、10:30……到16:30正好是8个小时。 预设2:画一画,我是画的,在时间轴上,从8:30到16:30正好经过了8个小时。 预设3:拨一拨,我是在钟表面上通过拨针的方法,数出开馆时间的。 预设3:算一算,我是计算的,16:30-8:30=8(时)。 小结:(课件出示)正如大家说的那样,天文馆每天从8:30开到16:30,中间正好经过了8个小时。 【教师注意:在进行解决问题的方法展示时,学生中可能出现多种解决的方法,不管学生用哪种方法,只要能推算出天文馆的开放时间,教师都要给予肯定,最后在通过交流完善和优化自己的推算方法。】 优化算法:理解什么是经过的时间。 师提问:谁能汇报一下什么是经过时间?它指的什么? 预设:天文馆一天开放的时间是指从开馆8:30到闭馆16:30所用的时间。师小结:“时间”是指从某一个时刻到另一个时刻的间隔,也就是经过的时间。教师适时讲解结束的时刻与开始的时刻,学生总结计算公式。 经过时间=结束的时刻-开始的时刻。(板书)16:30-8:30=8。 思考:这个8能写成8:00吗? 2.理解单位的写法 预设1:不可以,8:00表示8时这一个时刻。 预设2:不可以,从8:30数到16:30经过的是8个小时,而不是8点钟。 小结:从8:30数到16:30经过的是8个小时,而不是8点钟。因此单位应该写上时(板书)。 四、抽象概括、总结提升 1.学习借位计算 解决问题:《小丽访问哈勃》播放了多长时间?这个题目和前两个相同吗? 预设1:我是数的,从15:45数到16:30不够1小时,是45分钟。 预设2:这个题目与前面的不一样,这个题目中,分钟不够减的,我的列式是16:30-15:45。 小结:当分钟不够减时,我们该怎么办呢?引出学习问题。 预设1:15:45数到16:30不够1小时,是45分钟。 预设2:可以列竖式计算,30减45不够,根据以前所学是减法计算方法,可以上前一位借1,1个小时=60分,所以,90-45=45(分)。 (板书) 16时30分 — 15时45分 45分 小结:15:45数到16:30不够1小时,利用竖式可以这样计算,教师边板书边讲解:30分减去45分不够,可以像前一位借1,此时的1是1小时,需要转化为分钟,因为1个小时=60分,所以,借来了60分,60分加上原来的30分,一共是90分,90-45=45(分) 2. 总结方法 总结:在 解决经过时间的计算时,可以借助原来的加减法进行解决,根据以前所学是减法计算方法,当不够减时,可以上前一位借1,此时的1是1小时,需要转化为分钟,1个小时=60分,(板书)1时=60分,因此,借“1”是“60”。 小结:同学们,这节课我们走进了天文馆,通过交流、展示、汇报、总结的方法,学习了时间的简单计算,大家可真棒!下面,新的挑战还在等待着我们!瞧! 五、巩固应用,拓展提高 1. 基础练习,巩固新知 (1)课本68页第3题: 营业时间 8:30—17:30 引导:看到这个牌子,你能了解到哪些信息?又能得出什么结论? 预设:银行储蓄业务上午8时30分开始营业,下午5时30分停止营业。 预设:如果我想办理业务,就不应该在下午5时30分才到,银行这个时候已经在整理了。 预设:这家银行每天的营业时间是17:30—8:30=9(小时) A城-B城发车时间表:5:30—17:30,每半小时发一趟车。 引导:最早是几时几分发车?最晚呢?每天首班车和末班车发车时间间隔多久? 预设:最早一趟是上午的5:30发车,最晚一趟是下午的5:30发车。 预设:首班车和末班车发车时间间隔为17:30—5:30=12(小时) 禁止汽车通行8:00—21:30 引导:从这个牌子上你能了解到哪些信息?又能得出什么结论? 预设:知道从上午8:00到晚上的9:30汽车不能通行。 预设:我知道其他时间汽车是可以通行的。 预设:汽车禁止通行的时间段长达21:30—8:00=13小时30分钟 【温馨提示】 计算第一题时,要先算出各自的时间,才能比较出哪一次播音时间最长。 综合练习,应用新知 (1) 解决:课本70页,第10题: 【教学建议】 先引导学生深入思考,明白题意,再弄清水路长与实际和船速的关系,然后推算时间,求两港间的水路长。推算时间的时候,可以先让学生通过讨论,找到简便合理的方法。 板书设计 简单的时间计算 16:30-8:30=8(时) 10:30-9:00=1时30分 16:30-15:45=45(分) 10时30分 16时30分 - 9时00分 - 15时45分 1时30分 45分 使用说明: 1.教学反思:回味课堂,我感觉亮点之处有: (1)“授之于鱼不如授之于渔”, 从已知算法形成未知的算法。 通过列竖式对经过时间进行减法计算,是在学生初步接触了整数的减法计算的基础上进行的学习,在不借位的经过时间列竖式计算中,,学生容易掌握并应用,而在借位计算中,教师要留给学生充足的时间,学生能够想到不够减,去借1,易错点在原有为借一来十,而时间为借一来六十,教师需要着重强调,学生能够通过自主探究,从已知整数减法算法形成未知的经过时间算法。 (2)学生自主探究,归纳总结形成算式,渗透数学的建模思想。 通过两个比较简单的例题,学生能非常直观地得出结论, 初步得出的计算经过时间的模型为“经过时间=结束的时刻-开始的时刻”。培养了学生归纳总结的能力,渗透数学的建模思想。 2.使用建议 (1)这里所说的简单的经过时间的计算主要是指用12时记时法或24时记时法表示两个时间之间的差。但对于学困生或缺乏实际生活经验的孩子来说,在运用这一模型时又会有这样的问题,如:小红上午8:00到学校,下午4:00放学回家,她在学校待了多长时间?一部分学生就用8:00-4:00=4小时,而忽略了下午4:00实际上是结束时间,要先转换成24时记时法—16:00。所以为了避免类似的错误,建议教师在讲述时着重强调学生用24时记时法列式。 (2)在进行探究进过时间的解决问题的方法展示时,学生中可能出现多种解决的方法,不管学生用哪种方法,只要能推算出天文馆的开放时间,教师都要给予肯定,最后在通过交流完善和优化自己的推算方法 3.需要破解的问题 如何引入才能让让学生主动动手拨钟表,数时间格确定经过时间;甚至于学生能自主利用手指数一数,得出经过时间。这一环节是学生最初认识经过时间的生活经验,也是最简单是数形结合思想的运用,所以希望学生能自己主动地去应用.查看更多