- 2021-11-12 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学下册 第26章二次函数的图象与性质
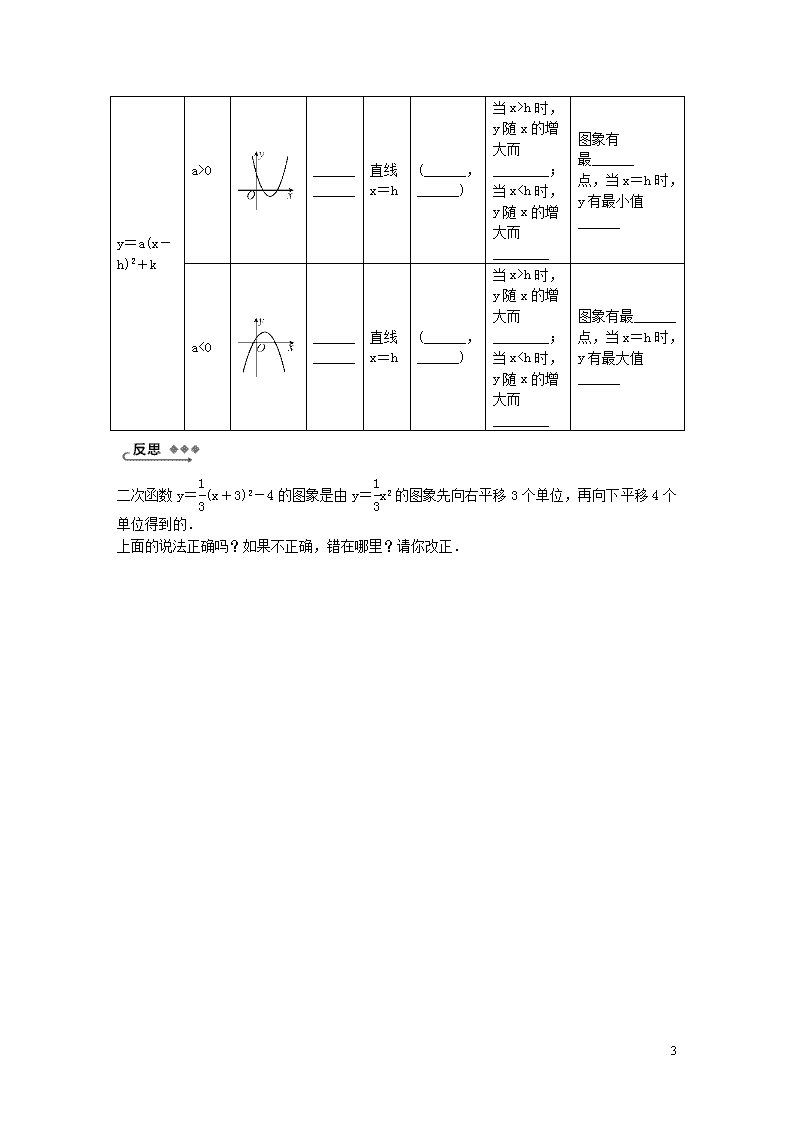
26.2 二次函数的图象与性质 2.二次函数y=ax2+bx+c的图象与性质 第3课时 二次函数y=a(x-h)2+k的图象与性质 知|识|目|标 1.通过阅读、操作、观察,能用描点法画二次函数y=a(x-h)2+k的图象. 2.通过比较、思考、讨论,能归纳出二次函数y=a(x-h)2+k图象的平移规律,并能确定平移后对应的函数关系式. 3.在准确画出二次函数y=a(x-h)2+k的图象的基础上,通过观察、探究、合作交流,能总结出二次函数y=a(x-h)2+k的性质并会熟练应用. 目标一 会画二次函数y=a(x-h)2+k的图象 例1 教材补充例题 在同一平面直角坐标系中画出下列函数的图象,并指出它们的开口方向、对称轴和顶点坐标. y=x2,y=(x-1)2,y=(x-1)2-2. 【归纳总结】画二次函数y=a(x-h)2+k的图象的技巧: (1)找到对称轴直线x=h(即顶点的横坐标h); (2)列表时选取的x值中把h放在中间,比h小和比h大的数各取若干个(一般取整数),并求出对应的y的值; (3)在平面直角坐标系里描出表中以(x,y)为坐标的点,并用光滑的曲线顺次连结. 目标二 掌握二次函数图象的平移规律 例2 教材补充例题 (1)把抛物线y=x2先向右平移2个单位,再向上平移3 6 个单位,平移后抛物线的关系式是____________; (2)将抛物线y=3(x-4)2+2先向右平移1个单位,再向下平移3个单位,平移后的抛物线的关系式是____________. 【归纳总结】求平移后的抛物线对应的函数关系式的方法: 首先要将二次函数的关系式化为顶点式,然后按照“左加右减,上加下减”的平移规律,确定平移后的抛物线对应的函数关系式. 目标三 理解二次函数y=a(x-h)2+k的性质 例3 高频考题 已知函数y=3+9. (1)确定此函数图象的开口方向、对称轴和顶点坐标; (2)当x=________时,函数有最________值,是________; (3)当x________时,y随x的增大而增大;当x________时,y随x的增大而减小; (4)求出该函数图象与y轴的交点坐标. 【归纳总结】二次函数y=a(x-h)2+k的性质: 二次函数y=a(x-h)2+k的图象是一条抛物线,它的开口方向、对称轴和顶点坐标与a,h,k的值有关. (1)当a>0时,开口向上;当a<0时,开口向下. (2)对称轴是直线x=h. (3)顶点坐标是(h,k). (4)当x=h时,函数有最大(或最小)值k. (5)若a>0,则当x<h时,y随x的增大而减小,当x>h时,y随x的增大而增大;若a<0,则当x<h时,y随x的增大而增大,当x>h时,y随x的增大而减小. 知识点一 二次函数y=a(x-h)2+k的图象与二次函数y=ax2的图象的关系 (1)形如y=a(x-h)2+k(a≠0)的关系式叫做二次函数的顶点式.二次函数y=a(x-h)2+k的图象与二次函数y=ax2的图象形状完全________,但位置不同,其顶点坐标为________,对称轴为直线________. (2)二次函数y=a(x-h)2+k的图象可由二次函数y=ax2的图象向右平移h(h>0)个单位[或向左平移|h|(h<0)个单位],再向上平移k(k>0)个单位[或向下平移|k|(k<0)个单位]得到. 知识点二 二次函数y=a(x-h)2+k的图象与性质 二次函数 a的符号 图象 图象的开口方向 图象的对称轴 图象的顶点坐标 函数值的变化情况 最值 6 y=a(x-h)2+k a>0 ______ ______ 直线 x=h (______, ______) 当x>h时,y随x的增大而________;当x查看更多