中考一轮复习教案之函数及其图象（三）9-14

中考一轮复习教案之函数及其图象（三）9-14

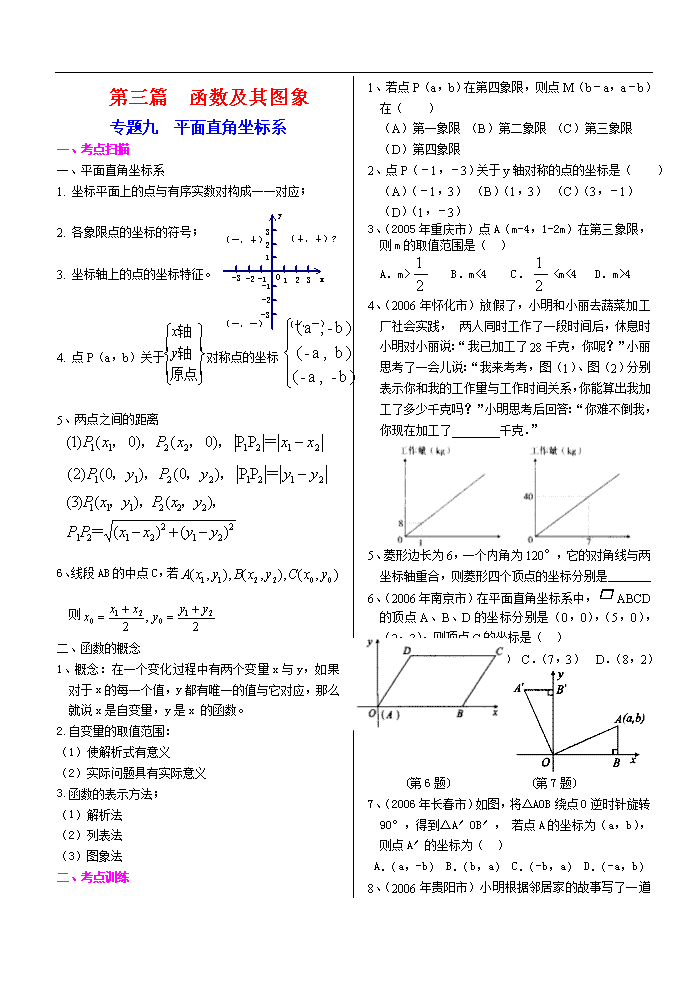
‎ 第三篇 函数及其图象 专题九 平面直角坐标系 一、考点扫描 一、平面直角坐标系 ‎1. 坐标平面上的点与有序实数对构成一一对应；‎ ‎2. 各象限点的坐标的符号；‎ ‎3. 坐标轴上的点的坐标特征。 ‎ ‎4. 点P（a，b）关于 对称点的坐标 ‎5、两点之间的距离 ‎6、线段AB的中点C，若 ‎ 则 二、函数的概念 ‎1、概念：在一个变化过程中有两个变量x与y，如果对于x的每一个值，y都有唯一的值与它对应，那么就说x是自变量，y是x 的函数。‎ ‎2.自变量的取值范围：‎ ‎（1）使解析式有意义 ‎（2）实际问题具有实际意义 ‎3.函数的表示方法；‎ ‎（1）解析法 ‎（2）列表法 ‎ ‎（3）图象法 二、考点训练 ‎1、若点P（a，b）在第四象限，则点M（b－a，a－b）在（ ）‎ ‎（A）第一象限 （B）第二象限 （C）第三象限 ‎（D）第四象限 ‎2、点P（－1，－3）关于y轴对称的点的坐标是（ ）‎ ‎（A）（－1，3） （B）（1，3） （C）（3，－1）‎ ‎ （D）（1，－3）‎ ‎3、（2005年重庆市）点A（m-4，1‎-2m）在第三象限，则m的取值范围是（ ）‎ ‎ A．m> B．m<‎4 C．4‎ ‎4、（2006年怀化市）放假了，小明和小丽去蔬菜加工厂社会实践，两人同时工作了一段时间后，休息时小明对小丽说：“我已加工了28千克，你呢？”小丽思考了一会儿说：“我来考考，图（1）、图（2）分别表示你和我的工作量与工作时间关系，你能算出我加工了多少千克吗？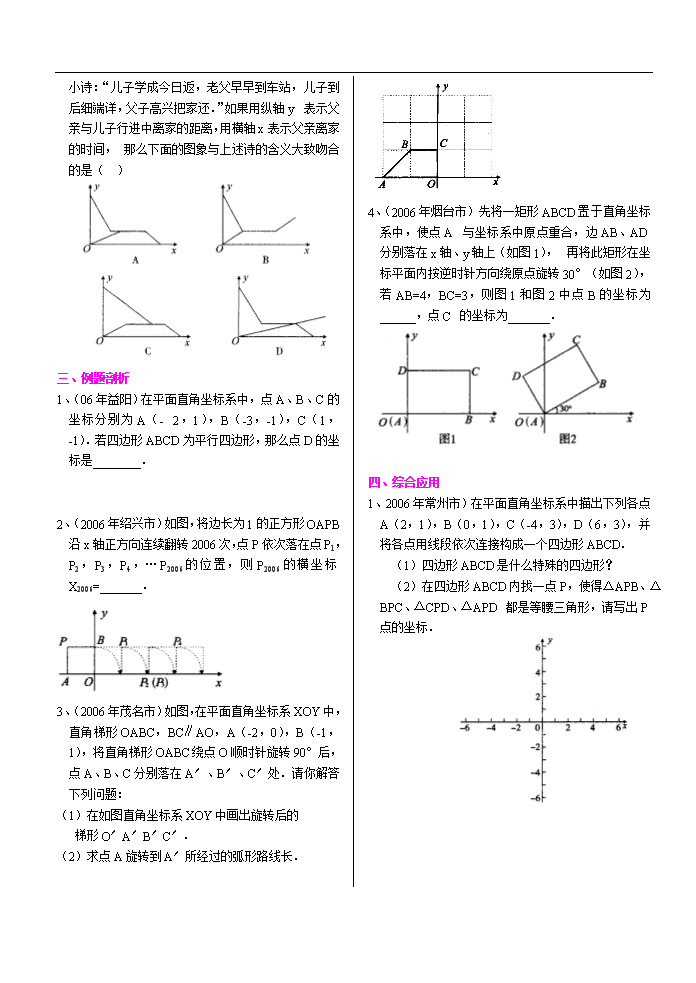”小明思考后回答：“你难不倒我，你现在加工了________千克．”‎ ‎5、菱形边长为6，一个内角为120°，它的对角线与两坐标轴重合，则菱形四个顶点的坐标分别是 ‎ ‎6、（2006年南京市）在平面直角坐标系中，ABCD的顶点A、B、D的坐标分别是（0，0），（5，0），（2，3），则顶点C的坐标是（ ）‎ A．（3，7） B．（5，3） C．（7，3） D．（8，2）‎ ‎(第6题) (第7题)‎ ‎7、（2006年长春市）如图，将△AOB绕点O逆时针旋转90°，得到△A′OB′，若点A的坐标为（a，b），则点A′的坐标为（ ）‎ ‎ A．（a，-b） B．（b，a） C．（-b，a） D．（-a，b）‎ ‎8、（2006年贵阳市）小明根据邻居家的故事写了一道小诗：“儿子学成今日返，老父早早到车站，儿子到后细端详，父子高兴把家还．”如果用纵轴y表示父亲与儿子行进中离家的距离，用横轴x表示父亲离家的时间，那么下面的图象与上述诗的含义大致吻合的是（ ）‎ 三、例题剖析 ‎1、（06年益阳）在平面直角坐标系中，点A、B、C的 坐标分别为A（-2，1），B（-3，-1），C（1，-1）．若四边形ABCD为平行四边形，那么点D的坐标是________．‎ ‎2、（2006年绍兴市）如图，将边长为1的正方形OAPB沿x轴正方向连续翻转2006次，点P依次落在点P1，P2，P3，P4，…P2006的位置，则P2006的横坐标X2006=_______．‎ ‎3、（2006年茂名市）如图，在平面直角坐标系XOY中，直角梯形OABC，BC∥AO，A（-2，0），B（-1，1），将直角梯形OABC绕点O顺时针旋转90°后，点A、B、C分别落在A′、B′、C′处．请你解答下列问题：‎ ‎（1）在如图直角坐标系XOY中画出旋转后的 梯形O′A′B′C′．‎ ‎（2）求点A旋转到A′所经过的弧形路线长．‎ ‎4、（2006年烟台市）先将一矩形ABCD置于直角坐标系中，使点A与坐标系中原点重合，边AB、AD分别落在x轴、y轴上（如图1），再将此矩形在坐标平面内按逆时针方向绕原点旋转30°（如图2），若AB=4，BC=3，则图1和图2中点B的坐标为______，点C的坐标为_______．‎ 四、综合应用 ‎1、2006年常州市）在平面直角坐标系中描出下列各点A（2，1），B（0，1），C（-4，3），D（6，3），并将各点用线段依次连接构成一个四边形ABCD．‎ ‎ （1）四边形ABCD是什么特殊的四边形？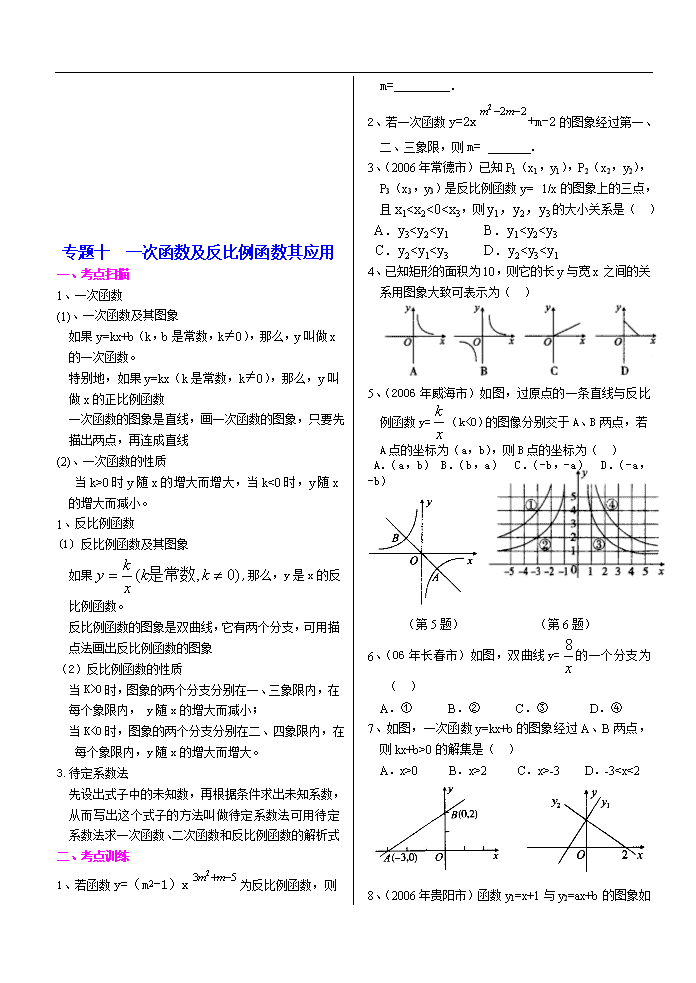‎ ‎ （2）在四边形ABCD内找一点P，使得△APB、△BPC、△CPD、△APD都是等腰三角形，请写出P点的坐标．‎ 专题十 一次函数及反比例函数其应用 一、考点扫描 ‎1、一次函数 ‎(1)、一次函数及其图象 如果y=kx+b（k，b是常数，k≠0），那么，y叫做x的一次函数。‎ 特别地，如果y=kx（k是常数，k≠0），那么，y叫做x的正比例函数 ‎ 一次函数的图象是直线，画一次函数的图象，只要先描出两点，再连成直线 ‎(2)、一次函数的性质 ‎ 当k>0时y随x的增大而增大，当k<0时，y随x 的增大而减小。‎ ‎1、反比例函数 ‎(1) 反比例函数及其图象 ‎ 如果,那么，y是x的反比例函数。‎ 反比例函数的图象是双曲线，它有两个分支，可用描点法画出反比例函数的图象 ‎（2）反比例函数的性质 当K>0时，图象的两个分支分别在一、三象限内，在每个象限内， y随x的增大而减小；‎ ‎ 当K<0时，图象的两个分支分别在二、四象限内，在每个象限内，y随x的增大而增大。‎ ‎3.待定系数法 ‎ 先设出式子中的未知数，再根据条件求出未知系数，从而写出这个式子的方法叫做待定系数法可用待定系数法求一次函数、二次函数和反比例函数的解析式 二、考点训练 ‎1、若函数y=（m2-1）x为反比例函数，则m=________．‎ ‎2、若一次函数y=2x+m-2的图象经过第一、二、三象限，则m= ．‎ ‎3、（2006年常德市）已知P1（x1，y1），P2（x2，y2），P3（x3，y3）是反比例函数y=1/x的图象上的三点，且x10的解集是（ ）‎ A．x>0 B．x>‎2 C．x>-3 D．-30；②c>0；③b2‎-4ac>0，其中正确的个数是（ ）‎ A．0个 B．1个 C．2个 D．3个 ‎7、（2006年常德市）根据下列表格中二次函数y=ax2+bx+c的自变量x与函数值y的对应值，判断方程ax2+bx+c=0（a≠0，a，b，c为常数）的一个解x的范围是（ ）‎ ‎ x ‎6.17‎ ‎6.18‎ ‎6.19‎ ‎6.20‎ y=ax2+bx+c ‎-0.03‎ ‎-0.01‎ ‎0.02‎ ‎0.04‎ A．60．‎ ‎4、（06年长春市）如图，P为抛物线y=x2-x+上对称轴右侧的一点，且点P在x轴上方，过点P作PA垂直x轴于点A，PB垂直y轴于点B，得到矩形PAOB．若AP=1，求矩形PAOB的面积．‎ 四、综合应用 ‎1、（2006年烟台市）如图（单位：m），等腰三角形ABC以‎2米/秒的速度沿直线L向正方形移动，直到AB与CD重合．设x秒时，三角形与正方形重叠部分的面积为ym2．‎ ‎（1）写出y与x的关系式；‎ ‎（2）当x=2，3.5时，y分别是多少？‎ ‎（3）当重叠部分的面积是正方形面积的一半时，三角形移动了多长时间？求抛物线顶点坐标、对称轴.‎ ‎ ‎ ‎2、（06年常州市）在平面直角坐标系中，已知二次函数y=a（x-1）2+k的图像与x轴相交于点A、B，顶点为C，点D在这个二次函数图像的对称轴上，若四边形ABCD是一个边长为2且有一个内角为60°的菱形，求此二次函数的表达式．‎ 专题十二 二次函数的应用 一、考点扫描 二次函数应用 二、例题剖析 ‎1、（2006年旅顺口区）已知边长为4的正方形截去一个角后成为五边形ABCDE（如图），其中AF=2，BF=1．试在AB上求一点P，使矩形PNDM有最大面积．‎ ‎ ‎ ‎2、某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：‎ x（元）‎ ‎15‎ ‎20‎ ‎30‎ ‎…‎ y（件）‎ ‎25‎ ‎20‎ ‎10‎ ‎…‎ ‎ 若日销售量y是销售价x的一次函数．‎ ‎（1）求出日销售量y（件）与销售价x（元）的函数关系式；‎ ‎（2）要使每日的销售利润最大，每件产品的销售价应定为多少元？此时每日销售利润是多少元？‎ ‎3、在距离地面‎2m高的某处把一物体以初速度V0（m/s）竖直向上抛出，在不计空气阻力的情况下，其上升高度s（m）与抛出时间t（s）满足：S=V0t-gt2（其中g是常数，通常取‎10m/s2），若V0=‎‎10m ‎/s，则该物体在运动过程中最高点距离地面________m．‎ ‎4、影响刹车距离的最主要因素是汽车行驶的速度及路面的摩擦系数．有研究表明，晴天在某段公路上行驶上，速度为V（km/h）的汽车的刹车距离S（m）可由公式S=V2确定；雨天行驶时，这一公式为S=V2．如果车行驶的速度是‎60km/h，那么在雨天行驶和晴天行驶相比，刹车距离相差_________米．‎ ‎5、（06年南京市）如图，在矩形ABCD中，AB=2AD，线段EF=10．在EF上取一点M，分别以EM、MF为一边作矩形EMNH、矩形MFGN，使矩形MFGN～矩形ABCD．令MN=x，当x为何值时，矩形EMNH的面积S有最大值？最大值是多少？‎ ‎6、（2006年青岛市）在2006年青岛崂山北宅樱桃节前夕，某果品批发公司为指导今年的樱桃销售，对往年的市场销售情况进行了调查统计，得到如下数据：‎ 销售价x（元/千克）‎ ‎…‎ ‎ 25‎ ‎ 24‎ ‎ 23‎ ‎ 22‎ ‎…‎ 销售量y（千克）‎ ‎…‎ ‎2000‎ ‎2500‎ ‎3000‎ ‎3500‎ ‎…‎ ‎（1）在直角坐标系内，作出各组有序数对（x，y）所对应的点．连接各点并观察所得的图形，判断y与x之间的函数关系，并求出y与x之间的函数关系式；‎ ‎（2）若樱桃进价为13元/千克，试求销售利润P（元）与销售价x（元/千克）之间的函数关系式，并求出当x取何值时，P的值最大？‎ ‎7、施工队要修建一个横断面为抛物线的公路隧道，其高度为‎6米，宽度OM为‎12米，现在O点为原点，OM所在直线为x轴建立直角坐标系（如图所示）．‎ ‎（1）直接写出点M及抛物线顶点P的坐标；‎ ‎（2）求出这条抛物线的函数解析式；‎ ‎（3）施工队计划在隧道门口搭建一个矩形“脚手架”ABCD，使A、D点在抛物线上，B、C点在地面OM上．为了筹备材料，需求出“脚手架”三根木杆AB、AD、DC的长度之和的最大值是多少？请你帮施工队计算一下．‎ 三、综合应用 ‎1、如图10，点在抛物线上，过点A作与 轴平行的直线交抛物线于点B，延长AO,BO分别与抛物线相交于点C,D，连接AD,BC，设点A的横坐标为m，且m>0．‎ ‎（1）当m=1时，求点A,B,D的坐标；‎ ‎（2）当m为何值时，四边形ABCD的两条对角线互相垂直；‎ ‎（3）猜想线段AB与CD之间的数量关系，并证明你的结论．‎ A x y B C O D 图10‎ ‎2、如图，已知抛物线与坐标轴交于A、B、C三点，点A的横坐标为-1，过点C(0,3)的直线与轴交于点Q，点P是线段BC上的一个动点，PH⊥OB于点H．若PB=5t，且0y2时，x的取值范围是_________．‎ ‎7．（2005年十堰市）在同一平面直角坐标系中，函数y=kx+k，y=（k>0）的图像大致是（ ）‎ ‎ ‎ ‎8．（2005年太原市）在反比例函数y=中，当x>0时，y随x的增大而增大，则二次函数y=kx2+2kx的图像大致是（ ）‎ 三、例题剖析 ‎1、（2005年海门市）某校八年级（1）班共有学生50人，据统计原来每人每年用于购买饮料的平均支出是a元．经测算和市场调查，若该班学生集体改饮某品牌的桶装纯净水，则年总费用由两部分组成，一部分是购买纯净水的费用，另一部分是其他费用780元，其中，纯净水的销售价（元/桶）与年购买总量y（桶）之间满足如图所示关系．‎ ‎ （1）求y与x的函数关系式；‎ ‎ （2）若该班每年需要纯净水380桶，且a为120时，请你根据提供的信息分析一下：该班学生集体改饮桶装纯净水与个人买材料，哪一种花钱更少？‎ ‎（3）当a至少为多少时，该班学生集体改饮桶装纯净水一定合算？从计算结果看，你有何感想（不超过30字）？‎ ‎2、一蔬菜基地种植的某种绿色蔬菜，根据今年的市场行情，预计从5月1日起的50天内，它的市场售价y1与上市时间x的关系可用图（a）的一条线段表示；它的种植成本y2与上市时间x的关系可用图（b）中的抛物线的一部分来表示．‎ ‎（1）求出图（a）中表示的市场售价y1与上市时间x的函数关系式．‎ ‎（2）求出图（b）中表示的种植成本y2与上市时间x的函数关系式．‎ ‎（3）假定市场售价减去种植成本为纯利润，问哪天上市的这种绿色蔬菜既不赔本也不赚钱？‎ ‎（市场售价和种植成本的单位：元/千克，时间单位：天）‎ ‎3、如图，一次函数y=ax+b的图象与反比例函数y=的图象交于A、B两点，与x轴交于点C，与y轴交于点D．已知OA=，tan∠AOC=‎ ‎，点B的坐标为（，-4）．‎ ‎ （1）求反比例函数和一次函数的解析式；‎ ‎（2）求△AOB的面积．‎ 三、综合应用 ‎1、（2006年潍坊市）为保证交通完全，汽车驾驶员必须知道汽车刹车后的停止距离（开始刹车到车辆停止车辆行驶的距离）与汽车行驶速度（开始刹车时的速度）的关系，以便及时刹车．下表是某款车在平坦道路上路况良好刹车后的停止距离与汽车行驶速度的对应值表：‎ 行驶速度（千米/时）‎ ‎40‎ ‎60‎ ‎80‎ ‎…‎ ‎ 停止距离（米）‎ ‎16‎ ‎30‎ ‎48‎ ‎…‎ ‎ （1）设汽车刹车后的停止距离y（米）是关于汽车行驶速度x（千米/时）的函数．给出以下三个函数①y=ax+b；②y=（k≠0）；③y=ax2+bx，请选择恰当的函数来描述停止距离y（米）与汽车行驶速度x（千米/时）的关系，说明选择理由,并求出符合要求的函数的解析式；‎ ‎ （2）根据你所选择的函数解析式，若汽车刹车后的停止距离为‎70米，求汽车行驶速度．‎ 专题十四 用函数的观点看方程（组）或不等式 一、考点扫描 二、考点训练 ‎1．（2006年广西省）已知y=-2x+m，当x=3时，y=1，则直线y=-2x+m与x轴的交点坐标为_______．‎ ‎2．若直线y=x-2与直线y=-x+a相交于x轴，则直线y=-x+a不经过的象限是_____．‎ ‎3．若不等式kx+b>0的解集为x>-2，则直线y=kx+b与x轴的交点为_____．‎ ‎4．（2006年衡阳市）如图，直线y1=k1x+b1与直线y2=k2x+b2交于点（-2，2），则当x____时，y10的解集为（ ）‎ ‎ A．x>0 B．x<‎0 C．x<2 D．x>2‎ ‎8．（2006年安徽省）已知甲、乙两弹簧的长度y（cm）与所挂物体质量x（kg）之间的函数解析式分别为y1=k1x+a1和y2=k2x+a2，图象如图所示，设所挂物体质量为‎2kg时，甲弹簧长为y1，乙弹簧长为y2，则y1与y2的大小关系为（ ）‎ ‎ A．y1>y2 B．y1=y‎2 C．y1y2．‎ ‎3、如图，平面直角坐标系中画出了函数y=kx+b的图象．‎ ‎（1）根据图象，求k，b的值；‎ ‎（2）在图中画出函数y=-2x+2的图象；‎ ‎（3）求x的取值范围，使函数y=kx+b的函数值大于函数y=-2x+2的函数值．‎ ‎4、育才中学需要添置某种教学仪器．方案1：到商 购买，每件需要8元；方案2：学校自己制作，每 件4元，另外需要制作工具的租用费120元．设需要 仪器x件，方案1与方案2的费用分别为y1，y2（元）．‎ ‎（1）分别写出y1，y2的函数表达式；‎ ‎（2）当购置仪器多少件时，两种方案的费用相同？‎ ‎（3）若学校需要仪器50件，问采用哪种方案便宜？请说明理由．‎ ‎5、如图表示一艘轮船和一艘快艇沿相同路线从甲港出 发到乙港行驶过程中路程随时间变化的图象（分别是 正比例函数图象和一次函数图象），根据图象解答下 列问题：‎ ‎（1）请分别求出表示轮船和快艇行驶过程的函数解析式（不要求写出自变量的取值范围）；‎ ‎（2）轮船和快艇在途中（不包括起点和终点）行驶的速度分别是多少？‎ ‎（3）问快艇出发多长时间赶上轮船？‎ 四、综合应用 ‎1、如图所示，设田地自动喷灌水管AB高出地面‎1.5米，在B处有一个自动旋转的喷水头，一瞬间喷出的水流是抛物线状，喷头B和水流最高点C的连线与水平地面成45°角，点C比B高出‎2米，在所建的坐标系中，求水流的落地点D到点A的距离是多少？‎ ‎2、某医药研究所开发了一种新药，在试验药效时发现，‎ ‎如果成人按规定剂量服用，那么服药后2小时时血液 中含药量最高，达每毫升6微克（1微克=10-3毫克），‎ ‎接着逐步衰减，10小时时血液中含药量为每毫升3‎ 微克，每毫升血液中含药量y（微克）随时间x（小时）的变化如图所示．当成人按规定剂量服药后:‎ ‎（1）分别求出x≤2和x≥2时x与y之间的函数关系式；‎ ‎（2）如果每毫升血液中含药量为4微克或4微克以上时在治疗疾病时是有效的，那么这个有效时间是多长？‎