2008年数学中考试题分类汇编(函数与几何图形2)
2008年中考试卷分类—函数与几何图形(2)
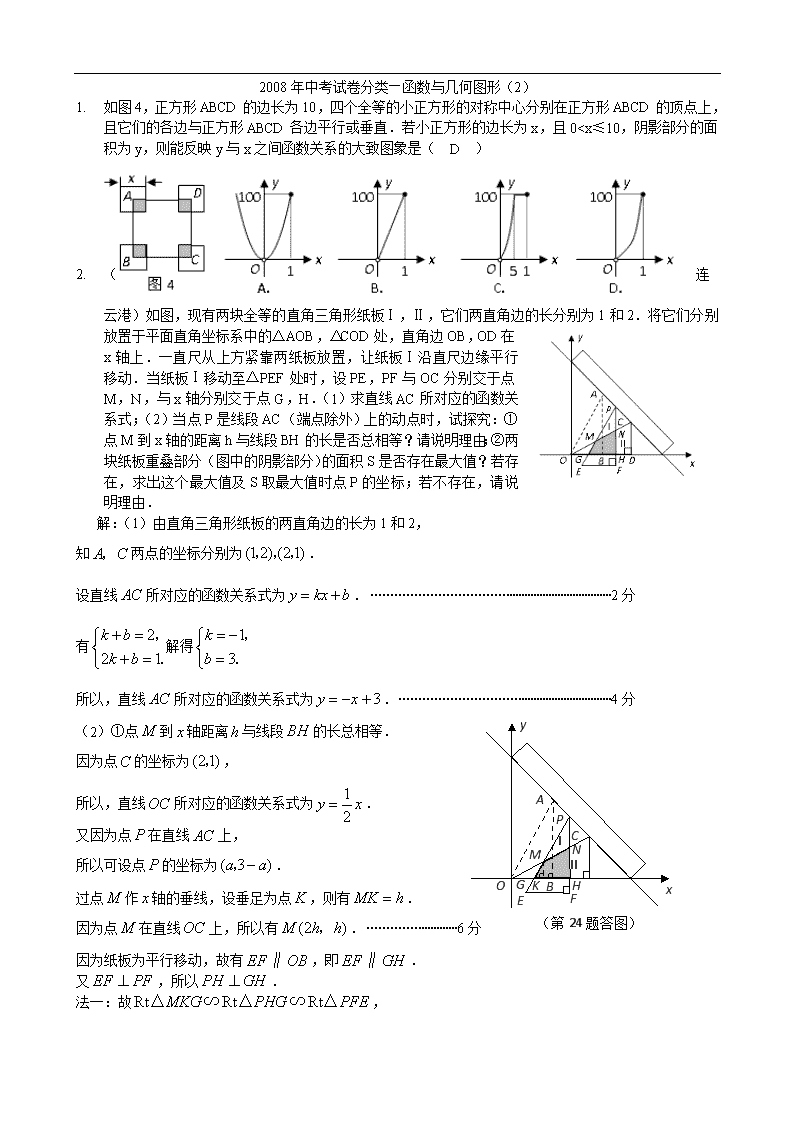
1. 如图4,正方形ABCD的边长为10,四个全等的小正方形的对称中心分别在正方形ABCD的顶点上,且它们的各边与正方形ABCD各边平行或垂直.若小正方形的边长为x,且0
0).(1)ΔABC中边BC上高AD= ((2)当x= 时,PQ恰好落在边BC上(如图1);(3)当PQ在ΔABC外部时(如图2),求y关于x的函数关系式(注明x的取值范围),并求出x为何值时y最大,最大值是多少?
解:(1); 2分
(2)(或); 6分
(3)设分别交于,则四边形为矩形.
A
B
C
M
N
P
Q
D
(第25题图2)
G
E
F
设,交于(如图2)
,.
,
.
,即
. 8分
. 10分
配方得:. 11分
当时,有最大值,最大值是6.
2. (宜昌)如图1,已知四边形OABC中的三个顶点坐标为O(0,0),A(0,n),C(m,0).动点P从点O出发依次沿线段OA,AB,BC向点C移动,设移动路程为z,△OPC的面积S随着z的变化而变化的图象如图2所示.m,n是常数, m>1,n>0.(1)请你确定n的值和点B的坐标;(2)当动点P是经过点O,C的抛物线y=
ax+bx+c的顶点,且在双曲线y=上时,求这时四边形OABC的面积.
.解:(1) 从图中可知,当P从O向A运动时,△POC的面积S=mz, z由0逐步增大到2,则S由0逐步增大到m,故OA=2,n=2 . (1分)
同理,AB=1,故点B的坐标是(1,2).(2分)
(2)解法一:
∵抛物线y=ax+bx+c经过点O(0,0),C(m ,0),∴c=0,b=-am,(3分)
∴抛物线为y=ax-amx,顶点坐标为(,-am2).(4分)
(25题图1)
如图1,设经过点O,C,P的抛物线为l.
当P在OA上运动时,O,P都在y轴上,
这时P,O,C三点不可能同在一条抛物线上,
∴这时抛物线l不存在, 故不存在m的值..①
当点P与C重合时,双曲线y=不可能经过P,
故也不存在m的值.②(5分)
(说明:①②任做对一处评1分,两处全对也只评一分)
当P在AB上运动时,即当02,与 x=≤1不合,舍去.(6分)③
容易求得直线BC的解析式是:,(7分)
当P在BC上运动,设P的坐标为 (x,y),当P是顶点时 x=,
故得y==,顶点P为(,),
∵1< x=2,又∵P在双曲线y=上,
于是,×=,化简后得5m-22m+22=0,
解得,,(8分)
与题意2
查看更多