呼和浩特专版2020中考数学复习方案第三单元函数及其图象第14课时二次函数的简单综合课件
第
14
课时
二次函数的简单综合
第三单元 函数及其图象
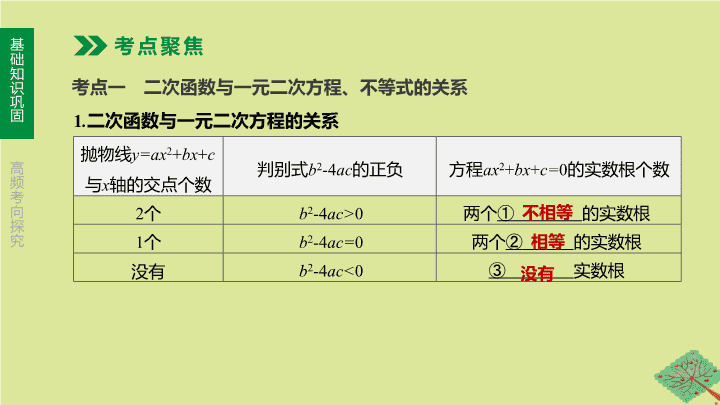
考点一 二次函数与一元二次方程、不等式的关系
考点聚焦
抛物线
y=ax
2
+
bx
+
c
与
x
轴的交点个数
判别式
b
2
-4
ac
的正负
方程
ax
2
+
bx
+
c=
0
的实数根个数
2
个
b
2
-4
ac>
0
两个
①
的实数根
1
个
b
2
-4
ac=
0
两个
②
的实数根
没有
b
2
-4
ac<
0
③
实数根
不相等
相等
没有
1
.
二次函数与一元二次方程的关系
2
.
二次函数与不等式的关系
(1)
ax
2
+
bx
+
c>
0
的解集
函数
y=ax
2
+
bx
+
c
的图象位于
x
轴上方的部分对应的点的横坐标的取值范围
.
(2)
ax
2
+
bx
+
c<
0
的解集
函数
y=ax
2
+
bx
+
c
的图象位于
④
的部分对应的点的横坐标的取值范围
.
x
轴下方
考点二 二次函数的综合应用
2
.
与几何图形结合
二次函数常常与三角形、四边形、圆等几何图形结合
,
考查以下几类问题
:
(1)
线段数量关系、最值问题
;
(2)
面积数量关系、最值问题
;
(3)
存在性问题
:
包含特殊三角形、特殊四边形、直线与圆相切等
.
题组 必会题
对点演练
图
1
4
-1
[
答案
]C
图
14-2
[
答案
]4
3
.
[
九上
P47
习题
22
.
2
第
5
题改编
]
如图
14-3
是函数
y=x
2
-2
x
-3
的图象
,
利用图象回答
:
(1)
方程
x
2
-2
x
-3
=
0
的解是
;
(2)
函数值大于
0
时
x
的取值范围是
;
(3)
函数值小于
0
时
x
的取值范围是
.
图
14-3
x
1
=
-1,
x
2
=
3
x<
-1
或
x>
3
-1
0,
由
a=b
-1
<
0,
得到
b<
1,
∴
0
0,
得到
a>
-1,
∴
-1
-3
C
.k<
3
D
.k>
3
图
14-5
[
答案
]D
6
.
[2019·
呼和浩特
16
题
]
对任意实数
a
,
若多项式
2
b
2
-5
ab
+3
a
2
的值总大于
-3,
则实数
b
的取值范围是
.
-6
4
2
.
已知二次函数
y
1
=x
2
+
mx
+
n
的图象经过点
P
(-3,1),
对称轴是经过
(-1,0)
且平行于
y
轴的直线
.
(1)
求
m
,
n
的值
;
(2)
如图
14-7,
一次函数
y
2
=kx
+
b
的图象经过点
P
,
与
x
轴交于点
A
,
与二次函数的图象交于另一点
B
,
点
B
在点
P
的右侧
,
PA
∶
PB=
1
∶
5,
求一次函数的解析式
;
(3)
直接写出
y
1
>y
2
时
x
的取值范围
.
图
14-7
2
.
已知二次函数
y
1
=x
2
+
mx
+
n
的图象经过点
P
(-3,1),
对称轴是经过
(-1,0)
且平行于
y
轴的直线
.
(2)
如图
14-7,
一次函数
y
2
=kx
+
b
的图象经过点
P
,
与
x
轴交于点
A
,
与二次函数的图象交于另一点
B
,
点
B
在点
P
的右侧
,
PA
∶
PB=
1
∶
5,
求一次函数的解析式
;
图
14-7
2
.
已知二次函数
y
1
=x
2
+
mx
+
n
的图象经过点
P
(-3,1),
对称轴是经过
(-1,0)
且平行于
y
轴的直线
.
(3)
直接写出
y
1
>y
2
时
x
的取值范围
.
图
14-7
(3)
由图象可知
,
当
x<
-3
或
x>
2
时
,
y
1
>y
2
.
图
14-8
图
14-8
图
14-8
图
14-8
考向三 二次函数与几何的综合
例
3
如图
14-9,
已知抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0),
C
(0,3)
三点
,
直线
l
是抛物线的对称轴
.
(1)
一元二次方程
ax
2
+
bx
+
c=
0
的解为
.
(2)
求抛物线的解析式
.
(3)
求抛物线的顶点
D
的坐标与对称轴
.
(4)
设点
P
是直线
l
上的一个动点
,
点
P
在何处时
,
PA
+
PC
最小
?
(5)
当
△
PAC
的周长最小时
,
求点
P
的坐标
.
(6)
在直线
l
上是否存在点
M
,
使
△
MAC
为等腰三角形
?
若存在
,
求出所有符合条件的点
M
的坐标
;
若不存在
,
请说明理由
.
图
14-9
x
1
=
-1,
x
2
=
3
.
例
3
如图
14-9,
已知抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0),
C
(0,3)
三点
,
直线
l
是抛物线的对称轴
.
(2)
求抛物线的解析式
.
图
14-9
(2)
∵抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0)
两点
,
∴设抛物线的解析式为
y=a
(
x
+1)(
x
-3),
又∵抛物线过点
C
(0,3),
∴
3
=
-3
a
,
解得
a=
-1,
∴抛物线解析式为
y=
-(
x
+1)(
x
-3),
即
y=
-
x
2
+2
x
+3
.
例
3
如图
14-9,
已知抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0),
C
(0,3)
三点
,
直线
l
是抛物线的对称轴
.
(3)
求抛物线的顶点
D
的坐标与对称轴
.
图
14-9
(3)
∵
y=
-
x
2
+2
x
+3
=
-(
x
-1)
2
+4,
∴
D
(1,4),
对称轴为直线
x=
1
.
例
3
如图
14-9,
已知抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0),
C
(0,3)
三点
,
直线
l
是抛物线的对称轴
.
(4)
设点
P
是直线
l
上的一个动点
,
点
P
在何处时
,
PA
+
PC
最小
?
图
14-9
(4)
如图
,
连接
BC
,
交直线
l
于点
P
,
连接
PA.
此时
PA
+
PC
最小
.
例
3
如图
14-9,
已知抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0),
C
(0,3)
三点
,
直线
l
是抛物线的对称轴
.
(5)
当
△
PAC
的周长最小时
,
求点
P
的坐标
.
图
14-9
例
3
如图
14-9,
已知抛物线
y=ax
2
+
bx
+
c
经过
A
(-1,0),
B
(3,0),
C
(0,3)
三点
,
直线
l
是抛物线的对称轴
.
(6)
在直线
l
上是否存在点
M
,
使
△
MAC
为等腰三角形
?
若存在
,
求出所有符合条件的点
M
的坐标
;
若不存在
,
请说明理由
.
图
14-9
|
考向精练
|
图
14-10
[
答案
]2
2
.
[2019·
呼和浩特模拟
]
已知抛物线
y=ax
2
+
bx
+
c
(
a
≠0)
经过点
A
(1,0),
B
(3,0),
C
(0,-3)
.
(1)
求抛物线的表达式及顶点
D
的坐标
.
(2)
如图
14-11
①
,
点
P
是直线
BC
上方抛物线上一动点
,
过点
P
作
y
轴的平行线
,
交直线
BC
于点
E
,
是否存在一点
P
,
使线段
PE
的长最大
?
若存在
,
求出
PE
长的最大值
;
若不存在
,
请说明理由
.
图
14-11
(3)
如图②
,
过点
A
作
y
轴的平行线
,
交直线
BC
于点
F
,
连接
DA
,
DB
,
四边形
OAFC
沿射线
CB
方向运动
,
速度为每秒
1
个单位长度
,
运动时间为
t
秒
,
当点
C
与点
B
重合时停止运动
.
设运动过程中四边形
OAFC
与四边形
ADBF
重叠部分的面积为
S
,
请求出
S
与
t
的函数关系式
.
图
14-11
2
.
[2019·
呼和浩特模拟
]
已知抛物线
y=ax
2
+
bx
+
c
(
a
≠0)
经过点
A
(1,0),
B
(3,0),
C
(0,-3)
.
(2)
如图
14-11
①
,
点
P
是直线
BC
上方抛物线上一动点
,
过点
P
作
y
轴的平行线
,
交直线
BC
于点
E
,
是否存在一点
P
,
使线段
PE
的长最大
?
若存在
,
求出
PE
长的最大值
;
若不存在
,
请说明理由
.
图
14-11
2
.
[2019·
呼和浩特模拟
]
已知抛物线
y=ax
2
+
bx
+
c
(
a
≠0)
经过点
A
(1,0),
B
(3,0),
C
(0,-3)
.
(3)
如图②
,
过点
A
作
y
轴的平行线
,
交直线
BC
于点
F
,
连接
DA
,
DB
,
四边形
OAFC
沿射线
CB
方向运动
,
速度为每秒
1
个单位长度
,
运动时间为
t
秒
,
当点
C
与点
B
重合时停止运动
.
设运动过程中四边形
OAFC
与四边形
ADBF
重叠部分的面积为
S
,
请求出
S
与
t
的函数关系式
.
图
14-11