- 2021-11-12 发布 |
- 37.5 KB |
- 2页

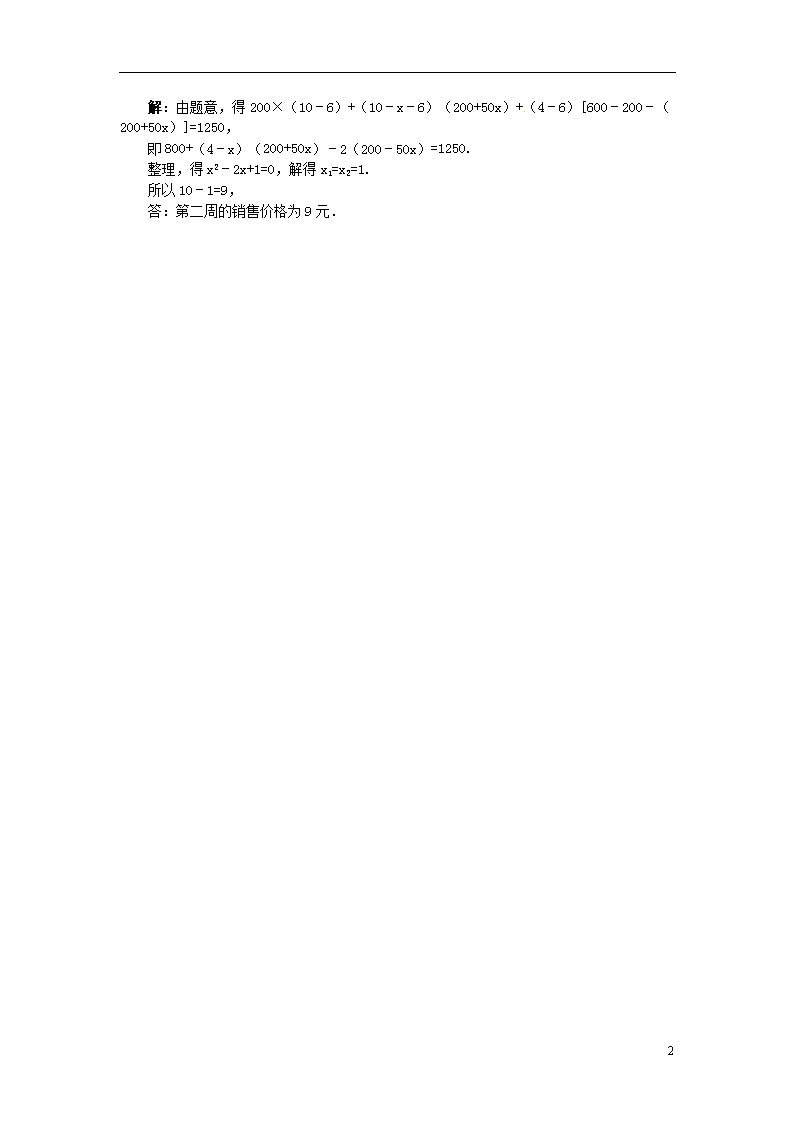
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020九年级数学上册 第二十一章 一元二次方程 寻找“等量”有“妙招”同步辅导素材新人教版
寻找“等量”有“妙招” 妙招一、抓住“关键句” 实际问题的关键句是指包含数量关系的句子,此句子中的等量关系是列方程的基础。 例1 “低碳生活,绿色出行”,自行车正逐渐成为人们喜爱的交通工具.某运动商城的自行车销售量自2013年起逐月增加,据统计,该商城1月份销售自行车64辆,3月份销售了100辆. 若该商城前4个月的自行车销量的月平均增长率相同,问该商城4月份卖出多少辆自行车? 分析: 本题的关键句是“3月份销售了100辆和前4个月的自行车销量的月平均增长率相同”,设前4个月自行车销量的月平均增长率为x,求出增长率即可求出4月份卖出自行车的数量. 解:设前4个月自行车销量的月平均增长率为x , 根据题意列方程,得64(1+x)2 =100 . 解得x=-225%(不合题意,舍去), x= 25% 100×(1+25%)=125(辆). 答:该商城4月份卖出125辆自行车。 妙招二、抓住“不变量” 在实际问题中,如果一个量不随问题的变化而变化,这个量就是不变量.于是我们可以依据这个不变量寻找等量关系. 例2 某超市将进货单价为40元的商品按50元出售,每天可买500个.如果这种商品每个涨价1元,其销售量就减少10个,如果超市为使这种商品每天赚得8000元的利润,商品的售价应定多少元? 分析:本题的中的不变量的每天赚得8000元的利润.相等关系是:每个商品的利润×销售数量=8000. 解:设该商品的售价为(50+x)元,则每个商品的利润为[(50+x)-40]元,销售数量为(500-10x)个,根据题意,得[(50+x)-40](500-10x)=8000. 解得x1=10,x2=30. 所以要赚得8000元的利润,这种商品的售价应定为60元或80元. 妙招三、借助表格 当实际问题中的数量较多,我们可以通过表格列出各种数量,通过表格中的数量关系列出方程. 例3 某商店购进600个旅游纪念品,进价为每个6元,第一周以每个10元的价格售出200个,第二周若按每个10元的价格销售仍可售出200个,但商店为了适当增加销量,决定降价销售(根据市场调查,单价每降低1元,可多售出50个,但售价不得低于进价),单价降低x元销售销售一周后,商店对剩余旅游纪念品清仓处理,以每个4元的价格全部售出,如果这批旅游纪念品共获利1250元,问第二周每个旅游纪念品的销售价格为多少元? 分析:本题题目比较长,为了更清楚地找到相等关系,进而列出方程,可列表如下: 周次 售价(元) 销售量(个) 利润(元) 第一周 10 200 (10-6)×200 第二周 10-x 200+50x (10-x-6)(200+5x) 两周后 4 600-200-(200+50x) (4-6)[(600-200-(200+50x)) 根据利润总和为1250可列出方程求解. 2 解:由题意,得200×(10﹣6)+(10﹣x﹣6)(200+50x)+(4﹣6)[600﹣200﹣(200+50x)]=1250, 即800+(4﹣x)(200+50x)﹣2(200﹣50x)=1250. 整理,得x2﹣2x+1=0,解得x1=x2=1. 所以10﹣1=9, 答:第二周的销售价格为9元. 2查看更多