2010年海淀区数学一模测试

2010年海淀区数学一模测试

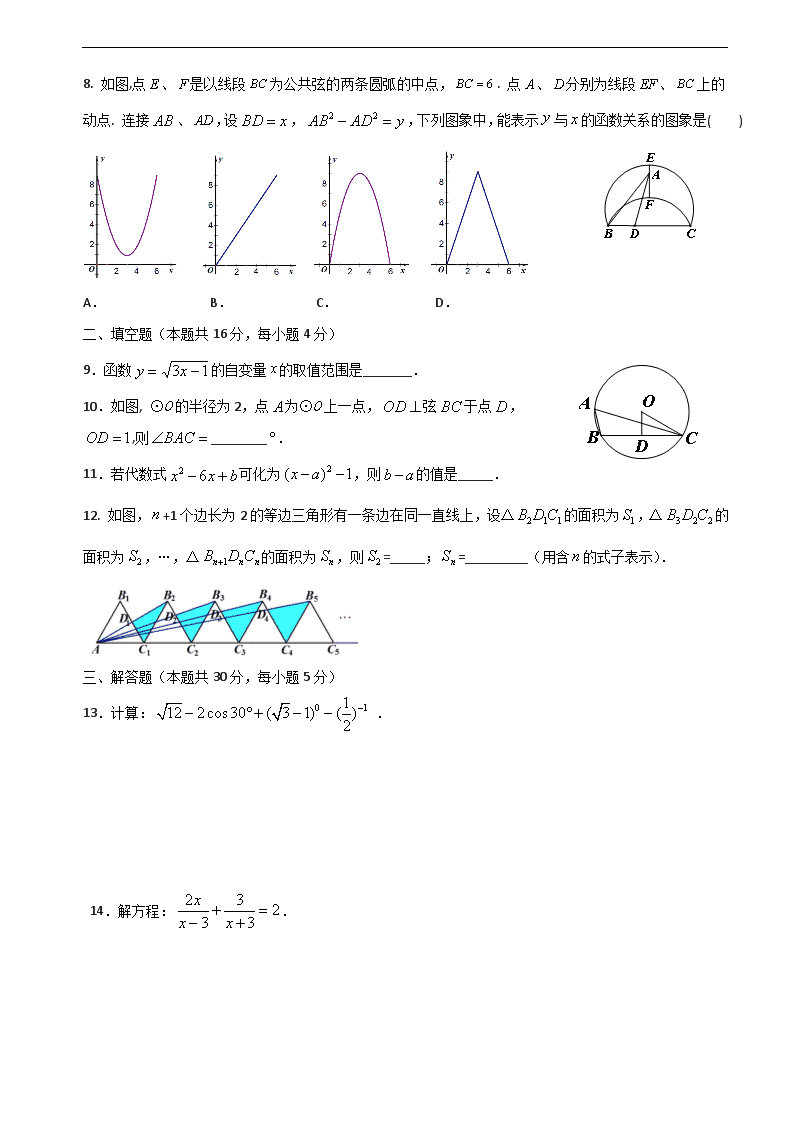
海 淀 区 九 年 级 第 二 学 期 期 中 测 评 数 学 ‎ 2010.5‎ 考生须知 ‎1．本试卷共5页，共五道大题，25道小题，满分120分.考试时间120分钟.‎ ‎2．在答题卡上准确填写学校名称、班级名称、姓名.‎ ‎3．试题答案一律填涂或书写在答题纸上，在试卷上作答无效.‎ ‎4．考试结束，请将本试卷、答题纸和草稿纸一并交回.‎ 一、选择题（本题共32分，每小题4分）‎ 下面各题均有四个选项，其中只有一个是符合题意的．‎ ‎1．的倒数是( )‎ A. 2 B. C. D.‎ ‎2．‎2010年2月12日至28日，温哥华冬奥会官方网站的浏览量为275 000 000人次. 将275 000 000用科学记数法表示为( )‎ A. B. C. D.‎ ‎3．右图是某几何体的三视图，则这个几何体是( )‎ A. 圆柱 B. 正方体 ‎ C. 球 D. 圆锥 ‎4．一个多边形的内角和是外角和的2倍，则这个多边形的边数为( )‎ A. 5 B.6 ‎ C. 7 D. 8‎ ‎5．一个布袋中有4个除颜色外其余都相同的小球，其中3个白球，1个红球．从袋中任意摸出1个球是白球的概率是( )‎ A． B． C． D．‎ ‎6． 四名运动员参加了射击预选赛，他们成绩的平均环数及其方差如表所示．如果选出一个成绩较好且状态稳定的人去参赛，那么应选( )‎ A．甲 B．乙 ‎ C．丙 D．丁 ‎7．把代数式 分解因式，结果正确的是( )‎ A． B． ‎ C． D．‎ ‎8. 如图,点、是以线段为公共弦的两条圆弧的中点，. 点、分别为线段、上的动点. 连接、，设，，下列图象中，能表示与的函数关系的图象是( )‎ ‎ ‎ A． B． C． D．‎ 二、填空题（本题共16分，每小题4分）‎ ‎9．函数的自变量的取值范围是_______． ‎ ‎10．如图, ⊙O的半径为2，点为⊙O上一点，弦于点， ‎ ‎,则________．‎ ‎11．若代数式可化为，则的值是_____．‎ ‎12. 如图，+1个边长为2的等边三角形有一条边在同一直线上，设△的面积为，△的面积为，…，△的面积为，则=_____；=_________（用含的式子表示）．‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算： ． ‎ ‎ 14．解方程：．‎ ‎15. 如图, △和△均为等腰直角三角形，‎ ‎, 连接、.‎ 求证: .‎ ‎ ‎ ‎16． 已知：，求代数式的值. ‎ ‎17. 已知：如图，一次函数与反比例函数的图象在第一象限的交点为．‎ ‎（1）求与的值；‎ ‎（2）设一次函数的图像与轴交于点，连接，求的度数．‎ ‎18. 列方程（组）解应用题：‎ ‎2009年12月联合国气候会议在哥本哈根召开．从某地到哥本哈根，若乘飞机需要3小时，若乘汽车需要9小时．这两种交通工具平均每小时二氧化碳的排放量之和为70千克，飞机全程二氧化碳的排放总量比汽车的多54千克，分别求飞机和汽车平均每小时二氧化碳的排放量． ‎ 四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）‎ ‎19．已知：如图，在直角梯形中，∥，，于点O，，求的长. ‎ ‎ ‎ ‎20. 已知：如图，⊙O为的外接圆，为⊙O的直径，作射线，使得平分，过点作于点.‎ ‎(1)求证：为⊙O的切线；‎ ‎(2)若，，求⊙O的半径. ‎ ‎21. 2009年秋季以来，我国西南地区遭受了严重的旱情,某校学生会自发组织了“保护水资源从我做起”的活动. 同学们采取问卷调查的方式，随机调查了本校150名同学家庭月人均用水量和节水措施情况.以下是根据调查结果做出的统计图的一部分.‎ 请根据以上信息解答问题：‎ ‎（1）补全图1和图2；‎ ‎（2）如果全校学生家庭总人数约为3000人，根据这150名同学家庭月人均用水量，估计全校学生家庭月用水总量. ‎ ‎ ‎ ‎ 图1 图2‎ ‎22．阅读：如图1，在和中，, ,、、、 四点都在直线上，点与点重合.‎ 连接、，我们可以借助于和的大小关系证明不等式：（）.‎ 图1‎ 图2‎ 证明过程如下: ‎ ‎∵‎ ‎∴‎ ‎∵,‎ ‎∴.‎ 即.‎ ‎∴. ‎ ‎∴.‎ 解决下列问题：‎ ‎（1）现将△沿直线向右平移，设,且.如图2,当时, _______.利用此图,仿照上述方法,证明不等式：（）.‎ ‎（2）用四个与全等的直角三角形纸板进行拼接，也能够借助图形证明上述不等式.请你画出一个示意图，并简要说明理由.‎ 五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）‎ ‎23．关于的一元二次方程有实数根，且为正整数.‎ ‎（1）求的值；‎ ‎（2）若此方程的两根均为整数，在平面直角坐标系中,抛物线与轴交于、两点（在左侧），与轴交于点. 点为对称轴上一点，且四边形为直角梯形，求的长；‎ ‎（3）将（2）中得到的抛物线沿水平方向平移，设顶点的坐标为,当抛物线与（2）中的直角梯形只有两个交点，且一个交点在边上时，直接写出的取值范围.‎ ‎24. 点为抛物线(为常数，)上任一点，将抛物线绕顶点逆时针旋转后得到的新图象与轴交于、两点（点在点的上方），点为点旋转后的对应点.‎ ‎（1）当，点横坐标为4时，求点的坐标；‎ ‎（2）设点，用含、的代数式表示；‎ ‎（3) 如图，点在第一象限内, 点在轴的正半轴上，点为的中点， 平分，，当时，求的值.‎ ‎25.已知：中，，中，,. 连接、，点、、分别为、、的中点.‎ ‎(1) 如图1，若、、三点在同一直线上，且，则的形状是________________，‎ 此时________；‎ ‎ ‎ 图1 图2‎ ‎(2) 如图2，若、、三点在同一直线上，且，证明，并计算的值（用含的式子表示）；‎ ‎(3) 在图2中，固定，将绕点旋转，直接写出的最大值.‎ 海淀区九年级第二学期期中测评 数学试卷答案及评分参考 一、选择题（本题共32分，每小题4分） ‎ 题 号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答 案 B C D B A B D C ‎ 二、填空题（本题共16分，每小题4分）‎ 题 号 ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答 案 ‎60‎ ‎5‎ 三、解答题（本题共30分，每小题5分）‎ ‎13．计算：.‎ 解： 原式=----------------------------------4分 ‎ =.---------------------------------5分 ‎14．解方程： .‎ 解：去分母，得 ． ---------------------------------1分 去括号，得． ---------------------------------2分 ‎ 解得 ． ---------------------------------4分 ‎ 经检验，是原方程的解．‎ ‎∴ 原方程的解是． ---------------------------------5分 ‎15．证明：∵ ∴ ---------------------------------1分 ‎∵ △与△均为等腰三角形，∴ ---------------------------------3分 在△和△中，‎ ‎∴ △≌△.---------------------------------4分 ‎∴ .---------------------------------5分 ‎16．解： 原式=---------------------------------2分 ‎ =.---------------------------------3分 ‎ 当时，‎ 原式=---------------------------------4分 ‎ .---------------------------------5分 ‎17．解：（1）∵点在双曲线上，∴.---------------------------------1分 又∵在直线上，∴ .------------2分 ‎（2）过点A作AM⊥x轴于点M.∵ 直线与轴交于点，∴ . 解得 .‎ ‎∴ 点的坐标为.‎ ‎∴ .---------------------------------3分 ‎∵点的坐标为， ∴.‎ 在Rt△中，,∴.∴.-------------------------4分 由勾股定理，得 .‎ ‎∴‎ ‎∴.‎ ‎∴.---------------------------------5分 ‎18．解：设乘飞机和坐汽车每小时的二氧化碳排放量分别是x千克和y千克. ………1分 依题意，得---------------------------------2分 解得----------------------------4分 答: 飞机和汽车每小时的二氧化碳排放量分别是‎57千克和‎13千克. ………5分 四、解答题（本题共20分，第19题5分，第20题5分，第21题6分，第22题4分）‎ ‎19．解法一：过点作交的延长线于点.-----------------------1分 ‎∴ .∵ 于点,∴ .∴ . ---------------2分 ‎∵ ，∴ 四边形为平行四边形. ---------------3分 ‎∴ .∵ ，‎ ‎∴ .-------------------------------4分 ‎∵ ，∴ . ∴ .--------------------------5分 解法二： ，‎ ‎ .又 ， . --------------------1分 ‎ 于点, . .‎ ‎ . .------------------------------------------2分 ‎ .---------------------------------------------3分 在Rt△中，.在Rt△中，.‎ ‎ .------------------------------------------4分 ‎ ,， . ---------------------------------------------5分 ‎20. （1）证明：连接. ---------------------------------1分 ‎∵ ，‎ ‎∴ . ∵ ，‎ ‎∴ . ∴ . ∴ ∥.--------------------------2分 ‎∵ ,∴ .∴ . ∵ 是⊙O半径，‎ ‎∴ 为⊙O的切线. ---------------------------------3分 ‎∵ ,，，∴ .‎ 由勾股定理，得. --------------------------------4分 ‎∴ .∵ 是⊙O直径，∴ .‎ ‎∴ .又∵ , ,‎ ‎∴ . 在Rt△中，==5.‎ ‎∴ ⊙O的半径为.-------------------------5分 ‎21. 解：(1)‎ ‎-------------------------2分 ‎--------------------------4分 ‎(2) 全体学生家庭月人均用水量为 ‎--------------------------5分 ‎（吨）.‎ 答：全校学生家庭月用水量约为 9040吨.--------------------------6分 ‎22．（1）；--------------------------1分 证明：连接、.‎ 可得.‎ ‎∴ ，‎ ‎. ‎ ‎∵ ，∴ ，即 .‎ ‎∴ . ∴ .--------------------------2分 ‎（2）答案不唯一，图1分，理由1分. ‎ 举例：如图，理由：‎ 延长BA、FE交于点I.‎ ‎ ∵ ，‎ ‎∴ ，‎ 即 .‎ ‎∴ .‎ ‎∴ .--------------------------4分 举例：如图，理由：‎ 四个直角三角形的面积和，‎ 大正方形的面积.∵ ，∴ .∴ .--------------------------4分 五、解答题（本题共22分，第23题7分，第24题8分，第25题7分）‎ ‎23．解：（1）∵关于的一元二次方程有实数根，‎ ‎∴ △=.∴ -----------------------1分 又∵ 为正整数，∴ . ------------------- 2分 ‎（2）∵ 方程两根均为整数，∴ .---------------3分 又∵ 抛物线与x轴交于A、B两点，∴ . ‎ ‎∴ 抛物线的解析式为.--------------4分 ‎∴ 抛物线的对称轴为.∵ 四边形为直角梯形，且，‎ ‎∴ ∥.∵ 点在对称轴上，∴ .--------------5分 ‎（3）或.----------- 7分（写对一个给1分）‎ ‎24. 解：（1）当m=2时，，则，. --------------------1分 如图，连接、,过点作轴于,过点作轴于.‎ 依题意,可得△≌△.‎ 则∴ .∴ . ------------------2分 ‎（2）用含的代数式表示：. ------4分 ‎（3）如图，延长到点E，使,连接.‎ ‎∵ 为中点,∴ .‎ ‎∵ ,∴ △≌△.‎ ‎∴ . ------------------5分 ‎∵ ,∴ .‎ ‎∵ 平分,∴ .‎ ‎∴ △≌△. ------------------6分 ‎∴ .∴ .------------------7分 ‎∵ 在新的图象上, ∴ .‎ ‎∴ ，（舍）.∴ . ------------------8分 ‎25. 解：(1)等边三角形，1；(每空1分) ------------------------2分 ‎（2）证明：连接、.‎ 由题意，得，,.‎ ‎∵ 、、三点在同一直线上，∴ 、、三点在同一直线上. ‎ ‎∴ .∵ 为中点，‎ ‎∴ 在Rt△中，.在Rt△中，. ∴ .-------------------------3分 ‎∴ 、、、四点都在以为圆心，为半径的圆上.∴ .‎ 又∵ ，∴ .∴ . -------------------4分 ‎∴ .由题意，，又.∴ .--------------------5分 ‎∴ . 在Rt中，.‎ ‎∵ ， ∴ .∴ .---------------6分 ‎（3）.--------------------------------7分 ‎ (注：本卷中许多问题解法不唯一,请老师根据评分标准酌情给分)‎