2020年黑龙江省绥化市中考数学试卷【含答案；word版本试题；可编辑】

2020年黑龙江省绥化市中考数学试卷【含答案；word版本试题；可编辑】

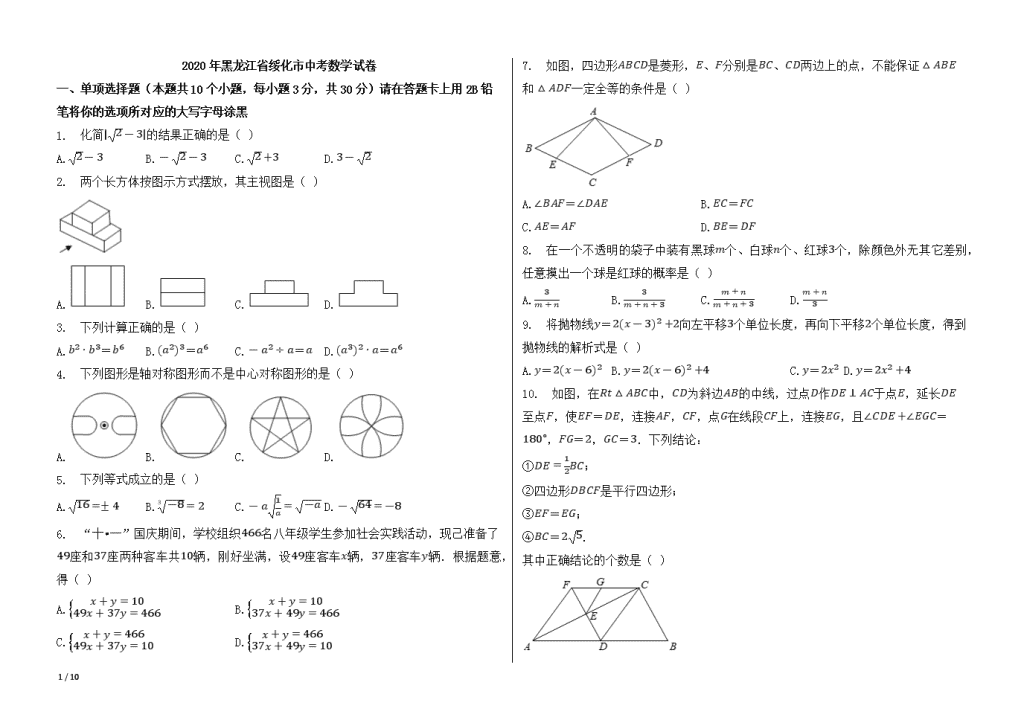
1 / 10 2020 年黑龙江省绥化市中考数学试卷 一、单项选择题（本题共 10个小题，每小题 3分，共 30分）请在答题卡上用 2B 铅 笔将你的选项所对应的大写字母涂黑 1. 化简 ㈮的结果正确的是（ ） A. ㈮ B. ㈮ C. ㈮ D.㈮ 2. 两个长方体按图示方式摆放，其主视图是（ ） A. B. C. D. 3. 下列计算正确的是（ ） A. ㈮＝ B.㈮＝ C. ＝ D.㈮ ＝ 4. 下列图形是轴对称图形而不是中心对称图形的是（ ） A. B. C. D. 5. 下列等式成立的是（ ） A. B. ㈮ C. D. 6. “十•一”国庆期间，学校组织 名八年级学生参加社会实践活动，现己准备 了 座和 ㈮ 座两种客车共 辆，刚好坐满，设 座客车 辆，㈮ 座客车 辆．根据题意，得（ ） A. ㈮ B. ㈮ C. ㈮ D. ㈮ 7. 如图，四边形  是菱形，、 分别是 、 两边上的点，不能保证  和  一定全等的条件是（ ） A.＝ B.＝ C.＝ D.＝ 8. 在一个不透明的袋子中装有黑球 个、白球 个、红球 ㈮ 个，除颜色外无其它 差别，任意摸出一个球是红球的概率是（ ） A. ㈮ B. ㈮ ㈮ C. ㈮ D. ㈮ 9. 将抛物线 ＝ ㈮ 向左平移 ㈮ 个单位长度，再向下平移 个单位长度， 得到抛物线的解析式是（ ） A.＝ B.＝ C.＝ D.＝ 10. 如图，在  中， 为斜边  的中线，过点  作  于点 ，延 长  至点 ，使 ＝，连接 ，，点 在线段 上，连接 ，且  ＝，＝，＝㈮．下列结论： ① ； ②四边形  是平行四边形； ③＝； ④＝ ． 其中正确结论的个数是（ ） 2 / 10 A. 个 B. 个 C.㈮ 个 D. 个 二、填空题（本题共 11 个小题，每小题 3 分，共 33 分）请在答题卡上把你的答案写 在相对应的题号后的指定区域内 11. XXXXXX 蔓延全球，截至北京时间 年 月 日，全球 XXXXXX 累计确诊病 例超过 例，数字 用科学记数法表示为________． 12. 甲、乙两位同学在近五次数学测试中，平均成绩均为 分，方差分别为 甲 ＝ 㤱， 乙 ＝㤱㈮，甲、乙两位同学成绩较稳定的是________同学． 13. 黑龙江省某企业用货车向乡镇运送农用物资，行驶 小时后，天空突然下起大 雨，影响车辆行驶速度，货车行驶的路程 与行驶时间 㤮的函数关系如图所示， 小时后货车的速度是 h㤮． 14. 因式分解：㈮ ＝________． 15. 已知圆锥的底面圆的半径是 㤱，母线长是 ，其侧面展开图的圆心角是 ________度． 16. 在  中，＝，若  ＝，＝，则  的长是________． 17. 在平面直角坐标系中，  和 的相似比等于 ，并且是关于原点 的 位似图形，若点 的坐标为标 ，则其对应点的坐标是________． 18. 在函数 ㈮ 中，自变量 的取值范围是________． 19. 如图，正五边形  内接于，点 为上一点（点 与点 ，点 不 重合），连接 、， ，垂足为 ， 等于________度． 20. 某工厂计划加工一批零件 个，实际每天加工零件的个数是原计划的 㤱 倍， 结果比原计划少用 天．设原计划每天加工零件 个，可列方程________． 21. 如图各图形是由大小相同的黑点组成，图 中有 个点，图 中有 个点，图 ㈮ 中有 个点，…，按此规律，第 个图中黑点的个数是________． 三、解答题（本题共 8个小题，共 57 分）请在答题卡上把你的答案写在相对应的题 号后的指定区域内 22. （1）如图，已知线段  和点 ，利用直尺和圆规作 ，使点 是  的内 心（不写作法，保留作图痕迹）； （2）在所画的  中，若＝，＝，＝，则  的内切圆半径是 ________． 3 / 10 23. 如图，热气球位于观测塔 的北偏西方向，距离观测塔 的 处，它 沿正南方向航行一段时间后，到达位于观测塔 的南偏西㈮方向的  处，这时， 处距离观测塔 有多远？（结果保留整数，参考数据：sin㈮ 㤱，cos㈮ 㤱，tan㈮ 㤱，sin 㤱，cos 㤱，tan 㤱．） 24. 如图，在边长均为 个单位长度的小正方形组成的网格中，点 ，点 ，点 均 为格点（每个小正方形的顶点叫做格点）． （1）作点 关于点 的对称点； （2）连接，将线段 绕点顺时针旋转得点  对应点，画出旋转后的线 段； （3）连接 ，求出四边形 的面积． 4 / 10 25. 为了解本校九年级学生体育测试项目“ 米跑”的训练情况，体育教师在 年 月份期间，每月随机抽取部分学生进行测试，将测试成绩分为：，， ， 四个等级，并绘制如图两幅统计图根据统计图提供的信息解答下列问题： （1）________月份测试的学生人数最少，________月份测试的学生中男生、女生人 数相等； （2）求扇形统计图中  等级人数占 月份测试人数的百分比； （3）若该校 年 月份九年级在校学生有 名，请你估计出测试成绩是 等 级的学生人数． 26. 如图，  内接于， 是直径，＝， 与  相交于点 ， 过点 作 ，垂足为 ，过点 作 ，垂足为 ，连接 、． （1）求证：直线  与 相切； （2）若   ，求 的值． 5 / 10 27. 如图，在矩形  中，＝，＝，点  是边  的中点，反比例函数 的图象经过点 ，交  边于点 ，直线  的解析式为＝ ． （1）求反比例函数 的解析式和直线  的解析式； （2）在 轴上找一点 ，使  的周长最小，求出此时点 的坐标； （3）在（2）的条件下，  的周长最小值是________． 28. 如图，在正方形  中，＝，点 在边  上，连接 ，作  于 点 ， 于点 ，连接 、，设＝，＝，  ． （1）求证：＝； （2）求证：tan＝ tan； （3）若点 从点  沿  边运动至点 停止，求点 ， 所经过的路径与边  围 成的图形的面积． 6 / 10 29. 如图 ，抛物线 与抛物线＝ 相交 轴于 点 ，抛物线与 轴交于 、 两点（点  在点 的右侧），直线＝ ㈮ 交 轴负半轴于点 ，交 轴于点，且 ＝． （1）求抛物线的解析式与 的值； （2）抛物线的对称轴交 轴于点 ，连接 ，在 轴上方的对称轴上找一点 ， 使以点 ，， 为顶点的三角形与 相似，求出  的长； （3）如图 ，过抛物线上的动点 作 轴于点 ，交直线＝ ㈮ 于点 ， 若点是点 关于直线 的对称点，是否存在点 （不与点 重合），使点落在 轴上？若存在，请直接写出点 的横坐标，若不存在，请说明理由． 7 / 10 参考答案与试题解析 2020 年黑龙江省绥化市中考数学试卷 一、单项选择题（本题共 10个小题，每小题 3分，共 30分）请在答题卡上用 2B 铅 笔将你的选项所对应的大写字母涂黑 1.D 2.C 3.B 4.C 5.D 6.A 7.C 8.B 9.C 10.二、填空题（本题共 11 个小题，每小题 3 分，共 33 分）请在答题卡上把你的答 案写在相对应的题号后的指定区域内 11.㤱 12.甲 13. 14. 15. 16. 17.标 或 标 18. ㈮ 且 19. 20. 㤱 21. 三、解答题（本题共 8个小题，共 57 分）请在答题卡上把你的答案写在相对应的题 号后的指定区域内 22.如图，  即为所求． 23.这时， 处距离观测塔 有 24.如图所示，点即为所求； 如图所示，线段即为所求； 如图，连接 ，过点 作 ，过点作 ，则 四边形 的面积   ＝． 25.,  等级人数占 月份测试人数的百分比是： ㈮ ； 根据题意得： ＝（名）， 答：测试成绩是 等级的学生人数有 名． 8 / 10 26.连接 ，如图， ∵  是 的直径， ∴ ＝， ∴  ＝， ∵ ＝， ∴ ＝， ∴  ＝， ∵ ＝，＝， ∴  ＝， 即＝， ∴ 直线  与 相切； ∵ ＝， ， ∴ ， ， ∵  ， ∴ ＝， ∵ ， ， ∴ ＝＝， ∴  ， ∴  ， ∵   ，＝， ∴ ， ∵ ， ∴ ， 27.∵ 点  是边  的中点，＝， ∴ ＝， ∵ 四边形  是矩形，＝， ∴ 标 ， ∵ 反比例函数 的图象经过点 ， ∴ ＝， ∴ 反比例函数的解析式为 ， 当 ＝ 时，＝， ∴ 标 ， 把 标 和 标 代入＝ 得， ， ∴ ， ∴ 直线  的解析式为 ＝ ； 作点  关于 轴的对称点 ，连接  交 轴于 ，连接 ， 此时，  的周长最小， ∵  点的坐标为标 ， ∴ 的坐标为 标 ， 设直线  的解析式为 ＝ ， ∴ ， 9 / 10 解得： ㈮ ㈮ ， ∴ 直线  的解析式为 ㈮ ㈮ ， 令 ＝，得 ㈮ ， ∴ 点 的坐标为标 ㈮ ； ㈮ 28.证明：在正方形  中，＝＝，＝＝， ∵  ， ， ∴ ＝＝， ∴  ＝， ∵  ＝， ∴ ＝， ∴  ， ∴ ＝； 在  和  中，tan  ，tan  ， ∴ tan tan     ． 由①可知＝，＝＝， ∴  ， ∴    ， 由①可知，＝， ∴     ， ∴     ， ∵   ，＝， ∴       ， ∴ tan tan ． ∴ tan＝tan． ∵  ， ， ∴ ＝＝， ∴ 当点 从点  沿  边运动至点 停止时，点 经过的路径是以  为直径， 圆心角为的圆弧， 同理可得点 经过的路径，两弧交于正方形的中心点 ，如图． ∵ ＝＝， ∴ 所围成的图形的面积为 ＝ ＝． 29.当 ＝ 时，得 ＝ ＝， ∴ 标 ， 把 标 代入＝ 得， ＝， ∴ ＝， ∴ ＝ ㈮ ， ∵ ＝， ∴ 标 ， 把 标 代入＝ ㈮ 中，得 ㈮＝， 解得， ㈮ ； ∴ 抛物线的解析式为＝ ㈮ ， 的值为 ㈮ ． 10 / 10 连接 ，如图 ， 令 ＝，得＝ ㈮ ＝， 解得，＝ 或 ， ∴ 标 ，标 ， ∴ 对称轴为： ㈮ ， ∴  ㈮ 标 ， ∴ ＝，＝， ㈮ ， ， ①当  时，   ，即  ， ∴  ， ②当  时，   ，即  ， ∴ ＝， 综上， 或 ； 点 的横坐标为 或 或 或 ． 如图，点是点 关于直线 的对称点，且点在 轴上时，由轴对称性质可知， ＝，＝，＝， ∵ 轴， ∴ hh 轴， ∴ ＝， ∴ ＝， ∴ ＝， ∴ ＝＝＝， ∴ 四边形 为菱形， ∴ hh ， 作 轴于点 ，设 标 ㈮ ，则 标 ㈮ ㈮， ∴ ＝，＝＝ ㈮ ㈮ ㈮ ＝ ， ∵ hh ， ∴ ＝， 在 中， ， ∴ sin＝sin ， ∴ ． 解得 ， ，㈮ ， ． 经检验， ， ，㈮ ， 都是所列方程的解． 综合以上可得，点 的横坐标为 或 或 或 ．