2012中考数学试题及答案分类汇编：函数的图像与性质

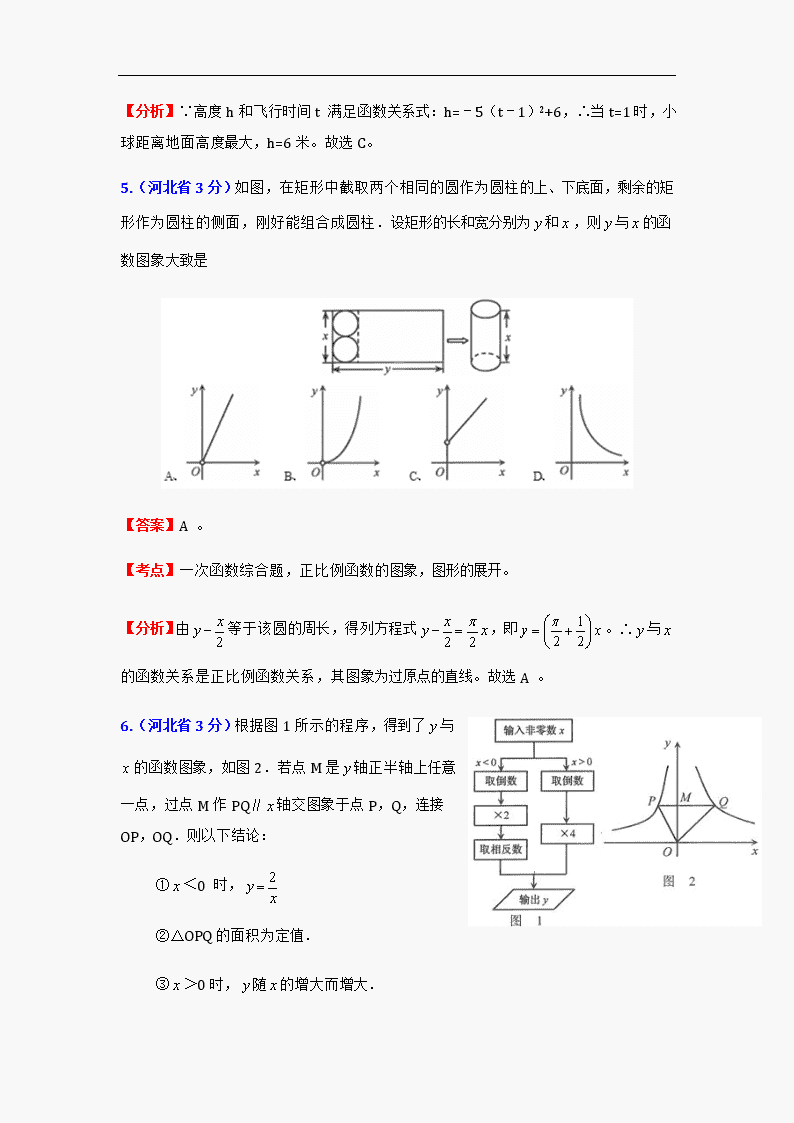
2012中考数学试题及答案分类汇编：函数的图像与性质

‎2012中考数学试题及答案分类汇编：‎ 函数的图像与性质 一、 选择题 ‎1.（北京4分）抛物线=2﹣6+5的顶点坐标为 ‎ A、（3，﹣4） B、（3，4） C、（﹣3，﹣4） D、（﹣3，4）‎ ‎【答案】A。‎ ‎【考点】二次函数的性质。‎ ‎【分析】利用配方法把抛物线的一般式写成顶点式，求顶点坐标，或者用顶点坐标公式求解：‎ ‎∵=2﹣6+5=2﹣6+9﹣9+5=（﹣3）2﹣4，∴抛物线=2+6+5的顶点坐标是（3，﹣4）．故选A。‎ ‎2.（天津3分）一家电信公司给顾客提供两种上网收费方式：方式A以每分0.1元的价格按上网所用时间计算；方式B除收月基费20元外．再以每分0．05元的价格按上网所用时间计费。若上网所用时问为分．计费为元，如图．是在同一直角坐标系中．分别描述两种计费方式的函救的图象，有下列结论：‎ ‎① 图象甲描述的是方式A：‎ ‎② 图象乙描述的是方式B；‎ ‎③ 当上网所用时间为500分时，选择方式B省钱．‎ 其中，正确结论的个数是 ‎ (A) 3 (B) 2 (C) 1 (D) 0‎ ‎【答案】A。‎ ‎【考点】一次函数的图象和性质。‎ ‎【分析】① 方式A以每分0.1元的价格按上网所用时间计算，函数关系式为=0.1，与图象甲描述的是方式相同，故结论正确；②方式B除收月基费20元外．再以每分0．05元的价格按上网所用时间计费，函数关系式为=0.05+20，与图象乙描述的是方式相同，故结论正确；③从图象观察可知，当>400时，‎ 乙<甲，所以当上网所用时间为500分时，选择方式B省钱，故结论正确。综上，选A。‎ ‎3.（河北省2分）一次函数y=6x+1的图象不经过 ‎ ‎ A、第一象限 B、第二象限 C、第三象限 D、第四象限 ‎【答案】D。‎ ‎【考点】一次函数的性质。‎ ‎【分析】由一次函数y=6x+1中k的符号，根据一次函数的性质，得：‎ ‎∵一次函数y=6x+1中k=6＞0，b=1＞0，‎ ‎∴此函数经过一、二、三象限。‎ 故选D。‎ ‎4.（河北省3分）一小球被抛出后，距离地面的高度h （米）和飞行时间t （秒）满足下面函数关系式：h=﹣5（t﹣1）2+6，则小球距离地面的最大高度是 ‎ ‎ A、‎1米 B、‎5米 C、‎6米 D、‎‎7米 ‎【答案】C。‎ ‎【考点】二次函数的应用，二次函数的最值。‎ ‎【分析】∵高度h和飞行时间t 满足函数关系式：h=﹣5（t﹣1）2+6，∴当t=1时，小球距离地面高度最大，h=6米。故选C。‎ ‎5.（河北省3分）如图，在矩形中截取两个相同的圆作为圆柱的上、下底面，剩余的矩形作为圆柱的侧面，刚好能组合成圆柱．设矩形的长和宽分别为和，则与的函数图象大致是 ‎ ‎【答案】A 。‎ ‎【考点】一次函数综合题，正比例函数的图象，图形的展开。‎ ‎【分析】由等于该圆的周长，得列方程式，即。∴与的函数关系是正比例函数关系，其图象为过原点的直线。故选A 。 ‎6.（河北省3分）根据图1所示的程序，得到了与的函数图象，如图2．若点M是轴正半轴上任意一点，过点M作PQ∥轴交图象于点P，Q，连接OP，OQ．则以下结论：‎ ‎①＜0 时， ‎②△OPQ的面积为定值．‎ ‎③＞0时，随的增大而增大．‎ ‎④MQ=2PM．‎ ‎⑤∠POQ可以等于90°．其中正确结论是 ‎ ‎ A、①②④ B、②④⑤ C、③④⑤ D、②③⑤‎ ‎【答案】B。‎ ‎【考点】反比例函数的性质，反比例函数图象上点的坐标特征，三角形的面积。‎ ‎【分析】由图1知，该函数为，据此分析：‎ ‎①、＜0，=，∴①错误；‎ ‎②、当＜0时，=，当＞0时，=，设P（，），Q（，d），‎ 则=﹣2，=4，∴△OPQ的面积是d=3，∴②正确；‎ ‎③、＞0时，随的增大而减小，∴③错误；‎ ‎④、∵=﹣2，=4，∴④正确；‎ ‎⑤、因为∠POQ=90°也行，∴⑤正确，正确的有②④⑤。故选B。‎ ‎7.（山西省2分）已知二次函数的图象如图所示，对称轴为直线=1，则下列结论正确的是 ‎ ‎ A， B．方程的两根是 ‎ C． D．当>0时，随的增大而减小．‎ ‎【答案】B。‎ ‎【考点】二次函数图象与系数的关系，抛物线与轴的交点。‎ ‎【分析】根据抛物线的开口方向，对称轴，与轴、轴的交点，逐一判断：‎ ‎ A、∵抛物线开口向下，与y轴交于正半轴，∴＜0，＞0，＜0，故本选项错误；‎ ‎ B、∵抛物线对称轴是=1，与轴交于（3，0），∴抛物线与轴另一交点为（－1，0），‎ 即方程的两根是，故本选项正确；‎ C、∵抛物线对称轴为，∴，故本选项错误；‎ ‎ D、∵抛物线对称轴为=1，开口向下，∴当＞1时，随的增大而减小，故本选项 错误。‎ 故选B。‎ ‎8.（内蒙古包头3分）已知二次函数y=ax2＋bx＋c同时满足下列条件：①对称轴是x=1；②最值是15；③二次函数的图象与x轴有两个交点，其横坐标的平方和为15﹣a，则b的值是 ‎ ‎ A、4或﹣30 B、﹣30 C、4 D、6或﹣20‎ ‎【答案】C。‎ ‎【考点】抛物线与x轴的交点，二次函数的性质，二次函数的最值，一元二次方程根与系数的关系。‎ ‎【分析】由已知，二次函数图象的顶点为（1，15），可设解析式为：y=a（x－1）2+15，‎ ‎ 即y=ax2－2x＋15＋a。‎ ‎ ∵二次函数的图象与x轴有两个交点，设为x1，x2，它们是ax2－2x＋15＋a=0的两个根。‎ ‎ ∴根据一元二次方程根与系数的关系，得x1＋x2=2，。‎ ‎ ∴。‎ ‎ ∵由已知，，∴，即。‎ ‎ 解得a=－2或15。‎ ‎ 当a=－2时，y=－2x2＋4x＋13，b=4；‎ ‎ 当a=15时，y=15x2－30x＋30，此时，图象开口向上，顶点为（1，15），与x轴没有交点，与已知不符。‎ ‎ ∴b=4。故选C。‎ ‎9.（内蒙古呼和浩特3分）已知一元二次方程的一根为，在二次函数的图象上有三点、、，、、的大小关系是 ‎ A. B. C. D. ‎ ‎【答案】A。‎ ‎【考点】二次函数图象上点的坐标特征，一元二次方程的解。‎ ‎【分析】把=﹣3代入中，得9﹣3﹣3=0，解得=2。‎ ‎∴二次函数解析式为。‎ ‎∴抛物线开口向上，对称轴为。‎ ‎∵＜﹣1＜＜，且﹣1﹣（）=，﹣（﹣1）=，而＞，‎ ‎∴。故选A。‎ ‎10.（内蒙古呼伦贝尔3分）双曲线经过点 ，则下列点在双曲线上的是 ‎ A. B. ( C. D. ‎ ‎【答案】D。‎ ‎【考点】曲线上点的坐标与方程的关系。‎ ‎【分析】根据点在曲线上，点的坐标满足方程的关系，将代入，求得，从而得到双曲线。将各点代入，易得在双曲线上，故选D。‎ ‎11.（内蒙古呼伦贝尔3分） 抛物线的顶点坐标 ‎ A．( 1, 1 ) B．C． D. ‎ ‎【答案】A。‎ ‎【考点】抛物线的性质。‎ ‎【分析】由顶点式直接得出抛物线的顶点坐标为( 1, 1 )。故选A。‎ 一、 填空题 ‎1. （天津3分）) 已知一次函数的图象经过点(0．1)．且满足随的增大而增大，则该一次函数的解析式可以为 ▲ (写出一一个即可)．‎ ‎【答案】（答案不唯一）。‎ ‎【考点】一次函数的图象和性质。‎ ‎【分析】根据一次函数的图象和性质，直接得出结果。答案不唯一，形如都可以。‎ ‎2.（内蒙古巴彦淖尔、赤峰3分）已知点A（﹣5，a），B（4，b）在直线y=﹣3x+2上，则a　 ▲ b．（填“＞”“＜”或“=”号 ）‎ ‎【答案】＞。‎ ‎【考点】一次函数的增减性，一次函数图象上点的坐标特征。‎ ‎【分析】根据一次函数的解析式判断出函数的增减性，再比较出﹣5与4的大小即可解答：‎ ‎∵直线y=﹣3x+2中，k=﹣3＜0，∴此函数是减函数。‎ ‎∵﹣5＜4，∴a＞b。‎ x y O C A B ‎3.（内蒙古包头3分）如图，点A(－1，m)和B(2，m＋3)在反比例函数的图象上，直线AB与轴的交于点C，则点C的坐标是　 ▲ 　．‎ ‎【答案】（1，0）。‎ ‎【考点】反比例函数与一次函数的交点问题，待定系数法，曲线上点的坐标与方程的关系。‎ ‎【分析】∵点A(－1，m)和B(2，m＋3)在反比例函数的图象上，‎ ‎∴，解得。∴A（﹣1，﹣2）与B（2，）。‎ 设直线AB的解析式为，则，解得。‎ ‎∴直线AB的解析式为。‎ 令=0，解得=。∴点C的坐标是（1，0）。‎ ‎4.（内蒙古呼和浩特3分）已知关于的一次函数的图象如图所示，则可化简为　 ▲ 　．‎ ‎【答案】。‎ ‎【考点】二次根式的性质与化简，绝对值，一次函数图象与系数的关系。‎ ‎【分析】根据一次函数图象与系数的关系，确定m、n的符号，然后由绝对值、二次根式的化简运算法则解得即可：‎ 根据图示知，关于的一次函数的图象经过第一、二、四象限，∴m＜0。‎ 又∵关于的一次函数的图象与轴交与正半轴，∴n＞0。‎ ‎∴。‎ ‎5.（内蒙古乌兰察布4分）函数l= (≥0 ) , （> 0 ）的图象如图所示，则结论： ① 两函数图象的交点A的坐标为（3 ,3 ) ② 当 > 3 ，时， ③ 当 ＝1时， BC = 8 ④ 当 逐渐增大时，l 随着 的增大而增大，2随着 的增大而减小．其中正确结论的序号是 ▲ .‎ ‎【答案】①③④。‎ ‎【考点】正比例函数和反正比例函数的图象特征。‎ ‎【分析】①由(> 0 )解得，从而。即两函数图象的交点A的坐标为（3 ,3 )。‎ ‎②当 > 3时，l= (≥0 ) 的图象在（> 0 ）的图象之上，所以。‎ ‎③ 当 ＝1时，l=1，，所以BC =8。‎ ‎④ 当 逐渐增大时，l 随着 的增大而增大，2随着 的增大而减小。‎ 因此，正确结论的序号是①③④。‎ 一、 解答题 ‎1.（北京5分）如图，在平面直角坐标系O中，一次函数=﹣2的图象与反比例函数的图象的一个交点为A（﹣1，n）．‎ ‎（1）求反比例函数的解析式；‎ ‎（2）若P是坐标轴上一点，且满足PA=OA，直接写出点P的坐标．‎ ‎【答案】解：（1）∵点A（﹣1，n）在一次函数=﹣2的图象上，‎ ‎∴n=﹣2×（﹣1）=2。‎ ‎ ∴点A的坐标为（﹣1，2）。‎ ‎ ∵点A在反比例函数的图象上，∴k=﹣2‎ ‎ ∴反比例函数的解析式是。‎ ‎ （2）点P的坐标为（﹣2，0）或（0，4）。‎ ‎【考点】反比例函数与一次函数的交点，待定系数法。‎ ‎【分析】（1）把A的坐标代入函数解析式即可求得k的值，即可得到函数解析式。 ‎ ‎ （2）以A为圆心，以OA为半径的圆与坐标轴的交点就是P。‎ ‎2.（北京7分）在平面直角坐标系Oy中，二次函数的图象与轴交于A、B两点（点A在点B的左侧），与轴交于点C．‎ ‎（1）求点A的坐标；‎ ‎（2）当∠ABC=45°时，求m的值；‎ ‎（3）已知一次函数=k+b，点P（n，0）是轴上的一个动点，在（2）的条件下，过点P垂直于轴的直线交这个一次函数的图象于点M，交二次函数 的图象于N．若只有当﹣2＜n＜2时，点M位于点N的上方，求这个一次函数的解析式．‎ ‎【答案】解：（1）∵点A、B是二次函数的图象与轴的交点，‎ ‎ ∴令=0，即m2+（m﹣3）﹣3=0解得1=﹣1，。 ‎ 又∵点A在点B左侧且m＞0，∴点A的坐标为（﹣1，0）。‎ ‎ （2）由（1）可知点B的坐标为，‎ ‎ ∵二次函数的图象与y轴交于点C，‎ ‎∴点C的坐标为（0，﹣3）。‎ ‎ ∵∠ABC=45°，∴。∴m=1。‎ ‎ （3）由（2）得，二次函数解析式为=2﹣2﹣3。‎ ‎ 依题意并结合图象可知，一次函数的图象与二次函数的图象交点的横坐标分别为﹣2和2。‎ ‎ 由此可得交点坐标为（﹣2，5）和（2，﹣3），‎ 将交点坐标分别代入一次函数解析式=k+b中，‎ 得，解得：。‎ ‎ ∴一次函数解析式为y=﹣2+1。‎ 【考点】二次函数综合题。‎ ‎【分析】（1）令=0则求得两根，又由点A在点B左侧且m＞0，所以求得点A的坐标。‎ ‎ （2）二次函数的图象与y轴交于点C，即求得点C，由∠ABC=45°，从而求得。‎ ‎ （3）由m值代入求得二次函数式，并能求得交点坐标，则代入一次函数式即求得。‎ ‎3.（天津8分）已知一次函数(b为常数)的图象与反比例函数（为常数．且）‎ 的图象相交于点P(3．1)．‎ ‎ (I) 求这两个函数的解析式；‎ ‎(II) 当>3时，试判断与的大小．井说明理由。‎ ‎【答案】解 ：(I)∵P(3．1)在一次函数一次函数上，∴1=3＋b。∴b=－2。‎ ‎ ∴一次函数的解析式为。‎ ‎ 同理，反比例函数的解析式为。‎ ‎ (II) ．理由如下：当时，，‎ ‎ 又当时．一次函数随的增大而增大．反比例函数随的增大而减小，‎ ‎ ∴当时。‎ ‎【考点】点的坐标与方程的关系，一次函数和反比例函数的性质。‎ ‎【分析】(I)因为点在曲线上点的坐标满足方程，所以利用点P在一次函数和反比例函数的图象上，把P的坐标分别代入即可求出。‎ ‎ (II)根据一次函数和反比例函数增减性的性质即可作出判断。‎ ‎4.（天津8分）‎ ‎ 注意：为了使同学们更好她解答本题，我们提供了—种分析问题的方法，你可以依照这个方法按要求完成本题的解答．也可以选用其他方法，按照解答题的一般要求进行解答即可．‎ ‎ 某商品现在的售价为每件35元．每天可卖出50件．市场调查反映：如果调整价格．每降价1元，每天可多卖出2件．请你帮助分析，当每件商品降价多少元时，可使每天的销售额最大，最大销售额是多少?‎ 设每件商品降价元．每天的销售额为元．‎ ‎(I) 分析：根据问题中的数量关系．用含的式子填表：‎ ‎ (Ⅱ) (由以上分析，用含的式子表示，并求出问题的解) ‎ ‎【答案】解：（Ⅰ）‎ ‎ ‎ ‎ （Ⅱ）根据题意，每天的销售额 ‎ 整理配方，得。‎ ‎ ∴当=5时，取得最大值1800。‎ ‎ 答：当每件商品降价5元时，可使每天的销售额最大，最大销售额为l 800元。‎ ‎【考点】列函数关系式，二次函数的应用。‎ ‎【分析】（Ⅰ）根据题意，可分析出结果。‎ ‎ （Ⅱ）列函数关系式是找出等量关系：‎ ‎ 每天的销售额=每件售价×每天销量 ‎ ‎ ‎ 求每件商品降价多少元时的每天的销售额最大和最大销售额是多少，只要把二次函数变形为顶点式的形式即可求出。‎ ‎5.（天津10分）在平面直角坐标系中．已知O坐标原点．点A(3．0)，B(0，4)．以点A为旋转中心，把△ABO顺时针旋转，得△ACD．记旋转转角为α．∠ABO为β．‎ ‎ (I) 如图①，当旋转后点D恰好落在AB边上时．求点D的坐标；‎ ‎ (Ⅱ) 如图②，当旋转后满足BC∥轴时．求α与β之闻的数量关系；‎ ‎(Ⅲ) 当旋转后满足∠AOD=β时．求直线CD的解析式(直接写出即如果即可)，‎ ‎ ‎ ‎【答案】解：(I)∵点A(3，0)，B(0，4)，∴0A=3，OB=4。‎ ‎ ∴在Rt△ABO中．由勾股定理．得AB=。‎ ‎ 根据题意，有DA=OA=3。‎ ‎ 如图①．过点D作DM⊥轴于点M，则MD∥OB。‎ ‎ ∴△ADM∽△ABO。有，‎ ‎ 得， 。‎ ‎ 又OM=OA-AM，得OM=。‎ ‎ ∴点D的坐标为（）。‎ ‎ (Ⅱ)如图②．由己知，得∠CAB=α，AC=AB，∴∠ABC=∠ACB。‎ ‎ ∴在△ABC中，由∠ABC+∠ACB+∠CAB=180°，得α=180°—2∠ABC。‎ ‎ 又∵BC∥轴，得∠OBC=90°，有∠ABC=90°—∠ABO=90°—β。‎ ‎ ∴α=180°—2（90°—β）=2β。‎ ‎ （Ⅲ） 直线CD的解析式为，或。‎ ‎【考点】旋转的性质，勾股定理，相似三角形的判定和性质，三角形内角和定理，平行的性质。‎ ‎【分析】(I)作辅助线DM⊥轴，由勾股定理求出AB的长，由相似三角形对应边成比例的性质即可求出。‎ ‎ (Ⅱ)由旋转的性质，知∠ABC=∠ACB，由三角形三内角和1800的定理可得α=180°—2∠ABC。又由于BC∥轴，可得∠ABC=90°—β，从而α=2β从而的关系。‎ ‎ ‎ 图1 图2‎ ‎（Ⅲ）如图1，连接BD，作DF⊥轴于F。由∠AOD=β=∠ABO可证△AOB≌△ADB，‎ ‎∴∠ADB=∠AOB=900。又∵∠ADC=900，∴B在直线CD上。‎ ‎∴可设直线CD方程式为=k+4。‎ 由△AOE∽△ABO得。‎ 设D点坐标为，则有 ‎，解之得 。‎ ‎ 代入直线CD方程=k+4，得k=。∴直线CD的解析式为。‎ ‎ 同样考虑∠AOD在轴下方的情况，如图2，可得直线CD的解析式。‎ ‎6.（河北省9分）已知A、B两地的路程为240千米．某经销商每天都要用汽车或火车将吨保鲜品一次 性由A地运往B地．受各种因素限制，下一周只能采用汽车和火车中的一种进行运输，且须提前预订．‎ 现有货运收费项目及收费标准表、行驶路程s（千米）与行驶时间t（时）的函数图象（如图1）、上周货运量折线统计图（如图2）等信息如下：‎ 货运收费项目及收费标准表 运输工具 运输费单价：元/（吨•千米）‎ 冷藏费单价：元/（吨•时）‎ 固定费用：元/次 汽车 ‎2‎ ‎5‎ ‎200‎ 火车 ‎1.6‎ ‎5‎ ‎2280‎ ‎ ‎ ‎（1）汽车的速度为60千米/时，火车的速度为100千米/时：‎ ‎（2）设每天用汽车和火车运输的总费用分别为汽（元）和火（元），分别求汽、火与 的函数关系式（不必写出的取值范围），及为何值时汽＞火（总费用=运输费+冷藏费+固定费用）‎ ‎（3）请你从平均数、折线图走势两个角度分析，建议该经销商应提前为下周预定哪种运输工具，才能使每天的运输总费用较省？‎ ‎【答案】解：（1）根据图表上点的坐标为：（2，120），（2，200），‎ ‎∴汽车的速度为 60千米/时，火车的速度为 100千米/时，‎ ‎（2）依据题意得出：‎ 汽=240·2+·5+200=500+200；‎ 火=240·1.6+·5+2280=396+2280。‎ 若汽＞火，得500+200＞396+2280，∴＞20。‎ ‎∴当＞20时，汽＞火。‎ ‎（3）∵上周货运量=（17+20+19+22+22+23+24）÷7=21＞20，‎ ‎∴从平均数分析，建议预定火车费用较省。‎ 又从折线图走势分析，上周货运量周四（含周四）后大于20且呈上升趋势，建议预订火车费用较省。‎ ‎【考点】一次函数的应用，折线统计图，算术平均数。‎ ‎【分析】（1）根据点的坐标为：（2，120），（2，200），直接得出两车的速度即可。‎ ‎（2）根据图表得出货运收费项目及收费标准表、行驶路程s（千米）与行驶时间t（时）的函数图象，得出关系时即可。‎ ‎（3）根据平均数的求法以及折线图走势两个角度分析得出运输总费用较省方案。‎ ‎7.（山西省7分）)如图，在平面直角坐标系中，一次函数的图象分别交轴、轴于A、B两点，与反比例函数的图象交于C、D两点，DE⊥轴于点E。已知C点的坐标是(6，)，DE=3．‎ ‎（1）求反比例函数与一次函数的解析式。‎ ‎（2）根据图象直接回答：当为何值时，一次函数的值大于反比例函数的值?‎ ‎【答案】解：（1）点C（6，－1）在反比例函数的图象上，∴=－6，‎ ‎∴反比例函数的解析式。‎ ‎∵点D在反比例函数上，且DE=3，∴=－2。∴点D的坐标为（－2，3）。‎ ‎∵C、D两点在直线上，∴，解得 。‎ ‎∴一次函数的解析式为。‎ ‎（2）由图象，得当x＜-2或0＜x＜6时，一次函数的值大于反比例函数的值。‎ ‎【考点】反比例函数与一次函数的交点问题 ‎【分析】（1）根据题意，可得出A、B两点的坐标，再将A、B两点的坐标代入与，即可得出解析式。‎ ‎（2）求当为何值时，一次函数的值大于反比例函数的值，即求出一次函数图象在反比例函数图象的上方时，的取值范围即可。‎ ‎8.（内蒙古呼和浩特8分）在同一直角坐标系中反比例函数的图象与一次函数的图象相交，且其中一个交点A的坐标为（–2，3），若一次函数的图象又与x轴相交于点B，且△AOB的面积为6（点O为坐标原点）.求一次函数与反比例函数的解析式.‎ ‎【答案】解：将点A（－2，3）代入中得：，∴。‎ K] ∴反比例函数的解析式为。‎ 又∵△AOB的面积为6，∴。 ∴∴|OB|=4。‎ ‎∴B点坐标为（4，0）或（－4，0）。‎ ‎①当B（4，0）时，又∵点A（－2，3）是两函数图象的交点，‎ ‎∴代入中得，解得。∴。‎ ‎②当B（－4，0）时，又∵点A（—2，3）是两函数图象的交点，‎ ‎∴代入中得，解得。 ∴。‎ 综上所述，一次函数的解析式为或。‎ ‎【考点】反比例函数与一次函数的交点问题，待定系数法，直线上点的坐标与方程的关系。‎ ‎【分析】将点A（﹣2，3）代入中得，得到=﹣2×3=﹣6，即得到反比例函数的解析式；由△AOB的面积为6，求出OB，得到B点坐标为（4，0）或（﹣4，0），然后分类讨论：一次函数过（﹣2，3）和（4，0）或一次函数过（﹣2，3）和（﹣4，0），利用待定系数法求出一次函数的解析式。‎ ‎9.（内蒙古巴彦淖尔、赤峰10分）如图，点D双曲线上，AD垂直轴，垂足为A，点C在AD上，CB平行于x轴交曲线于点B，直线AB与y轴交于点F，已知AC：AD=1：3，点C的坐标为（2，2）．‎ ‎（1）求该双曲线的解析式；‎ ‎（2）求△OFA的面积．‎ ‎【答案】解：（1）∵点C的坐标为（2，2），AD垂直x轴，‎ ‎∴AC=2。‎ 又∵AC：AD=1：3，∴AD=6。‎ ‎∴D点坐标为（2，6）。‎ 设双曲线的解析式为，‎ 把D（2，6）代入得，=2×6=12。‎ ‎∴双曲线解析式为。‎ ‎（2）设直线AB的解析式为，得 把A（2，0）和B（6，2）代入得，，解得。‎ ‎∴直线AB的解析式为。‎ 令=0，得=﹣1，∴F点的坐标为（0，﹣1）。‎ ‎∴S△OFC=×OA×OF=×2×1=1。‎ ‎【考点】反比例函数综合题，待定系数法，曲线上点的坐标与方程的关系。‎ ‎【分析】（1）由点C的坐标为（2，2）得AC=2，而AC：AD=1：3，得到AD=6，则D点坐标为（2，6），然后利用待定系数法确定双曲线的解析式。‎ ‎（2）已知A（2，0）和B（6，2），利用待定系数法确定直线AB的解析式，得到F点的坐标，然后利用三角形的面积公式计算即可。‎ ‎10.（内蒙古巴彦淖、赤峰尔12分）如图，直线y=x+3与坐标轴分别交于A，B两点，抛物线y=ax2+bx﹣3a经过点A，B，顶点为C，连接CB并延长交x轴于点E，点D与点B关于抛物线的对称轴MN对称．‎ ‎（1）求抛物线的解析式及顶点C的坐标；‎ ‎（2）求证：四边形ABCD是直角梯形．‎ ‎【答案】解：（1）∵y=x+3与坐标轴分别交与A、B两点，‎ ‎∴A点坐标（﹣3，0）、B点坐标（0，3）。‎ ‎∵抛物线y=ax2+bx﹣3a经过A、B两点，‎ ‎∴，解得。∴抛物线解析式为：y=﹣x2﹣2x+3。‎ ‎∵y=﹣x2﹣2x+3=﹣（x+1）2+4，‎ ‎∴顶点C的坐标为（﹣1，4）。‎ ‎（2）∵B、D关于MN对称，C（﹣1，4），B（0，3），∴D（﹣2，3）。‎ ‎∵B（3，0），A（﹣3，0），∴OA=OB。‎ 又∠AOB=90°，∴∠ABO=∠BAO=45°。‎ ‎∵B、D关于MN对称，∴BD⊥MN。‎ 又∵MN⊥X轴，∴BD∥X轴。‎ ‎∴∠DBA=∠BAO=45°。∴∠DBO=∠DBA+∠ABO=45°+45°=90°。‎ ‎∴∠ABC=180°﹣∠DBO=90°。∴∠CBD=∠ABC﹣∠ABD=45°。‎ ‎∵CM⊥BD，∴∠MCB=45°。‎ ‎∵B，D关于MN对称，∴∠CDM=∠CBD=45°，CD∥AB。‎ 又∵AD与BC不平行，∴四边形ABCD是梯形。‎ ‎∵∠ABC=90°，∴四边形ABCD是直角梯形。‎ ‎【考点】二次函数综合题，曲线上点的坐标与方程的关系，抛物线的顶点和对称轴，轴对称的性质，平行的判定和性质，直角梯形的判定。‎ ‎【分析】（1）先根据直线y=x+3求得点A与点B的坐标，然后代入二次函数的解析式求得其解析式，然后求得其顶点坐标即可。‎ ‎（2）根据B、D关于MN对称，C（﹣1，4），B（0，3）求得点D的坐标，然后得到AD与BC不平行，∴四边形ABCD是梯形，再根据∠ABC=90°得到四边形ABCD是直角梯形。‎ ‎11.（内蒙古呼伦贝尔6分）根据题意，解答问题： ‎ ‎（1）如图①，已知直线与轴、轴分别交于A、B两点，求勾股定理.‎ ‎（2）如图②，类比（1）的解题过程，请你通过构造直角三角形的方法，求出点M（3，4）与点 N（－2，1）之间的距离.‎ ‎【答案】解：（1）根据题意得， A（0，4），B（－2，O），‎ 在Rt△AOB中，根据勾股定理，得 ‎ 。‎ ‎（2）过M点作轴的垂线MF, 过N作轴的垂线NE, MF, NE交于点D 。‎ 由 M（3，4），N（－2，1），得 MD=， ND=。‎ ‎ ∴MN= 。‎ ‎【考点】直线上点的坐标与方程的关系，勾股定理。‎ ‎【分析】（1）由点在直线上，点的坐标满足方程的关系，可求出直线线与轴、轴的交点坐标，从而根据勾股定理求得勾股定理。‎ ‎ （2）构造直角三角形，过M点作轴的垂线MF, 过N作轴的垂线NE, MF, NE交于点D。‎ 在Rt△MND中，应用勾股定理即可求得点M（3，4）与点N（－2，1）之间的距离。‎