九年级数学下册第三章圆5直线和圆的位置关系第2课时习题课件北师大版

九年级数学下册第三章圆5直线和圆的位置关系第2课时习题课件北师大版

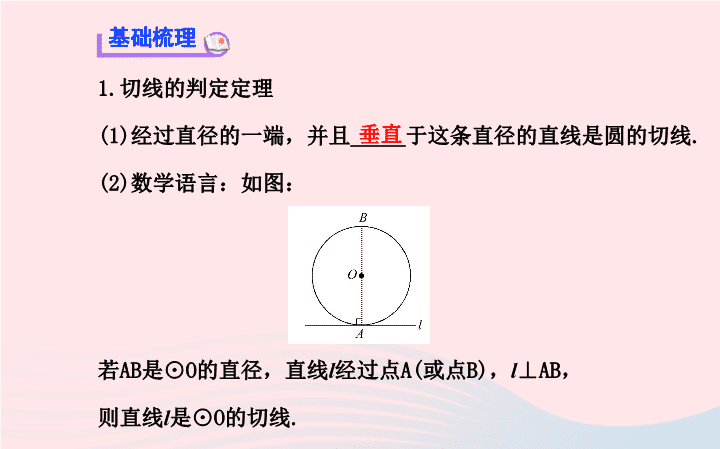
5 直线和圆的位置关系 第 2 课时 1. 探索圆的切线的判定方法，并会用切线的判定进行计算和证明． ( 重点、难点 ) 2. 作三角形内切圆的方法． ( 重点、难点 ) 1. 切线的判定定理 (1) 经过直径的一端，并且 _____ 于这条直径的直线是圆的切线 . (2) 数学语言：如图： 若 AB 是⊙ O 的直径，直线 l 经过点 A( 或点 B) ， l ⊥AB ， 则直线 l 是⊙ O 的切线 . 基础梳理 垂直 2. 三角形的内切圆 (1) 定义：和三角形的 ___ 边都相切的圆 . (2) 三角形的内心：内切圆的 _____ ，也即三角形的三条角平分线的交点 . (3) 三角形的内心的性质：到三角形 _____ 的距离相等 . 三 圆心 三边 ( 打“√”或“ ×”) (1) 圆有无数条切线，经过圆上一点只有一条切线 .( ) (2) 三角形的内心一定在三角形的内部 .( ) (3) 被直径垂直的直线都是圆的切线 .( ) (4) 一个三角形一定有且只有一个内切圆 . ( ) √ √ × √ 知识点 1 切线的判定 【 例 1】 如图，△ ABC 为等腰三角形， AB=AC ， O 是底边 BC 的中点，⊙ O 与腰 AB 相切于点 D ，求证： AC 与⊙ O 相切 . 【 解题探究 】 1. 已知⊙ O 的切线 AB 和切点 D ，连接 OD ，有何结论？ 提示： ∵ AB 切⊙ O 于 D ，∴ OD⊥AB ， OD 为⊙ O 的半径 . 2. 作 OE⊥AC, 垂足为 E. 怎样证明直线 AC 为⊙ O 的切线？ 提示： 连接 OA ，∵ AB=AC, OB=OC, ∴AO 平分∠ BAC ，∴ OE=OD ，∴ AC 与⊙ O 相切 . 【 总结提升 】 切线判定的两种思路 1. 连半径，证垂直：若已知直线与圆有公共点，则连接圆心与公共点，证明垂直 . 2. 作垂直，证等径：若直线与圆的公共点没有确定，则过圆心作直线的垂线，证明圆心到直线的距离等于圆的半径 . 知识点 2 三角形的内切圆 【 例 2】 如图 ,⊙O 是△ ABC 的内切圆 , 与 AB ， BC ， CA 分别相切于点 D ， E ， F,∠DEF=45°. 连接 BO 并延长交 AC 于点 G,AB=4,AG=2. (1) 求∠ A 的度数 . (2) 求⊙ O 的半径 . 【 思路点拨 】 (1) 连接 OF ， OD ，根据内切圆的性质及圆周角和圆心角的性质求出四边形三个角的角度，再确定∠ A. (2) 由△ BOD 和△ BGA 相似，根据相似三角形的对应边成比例，求出 OD 的长度，即圆的半径 . 【 自主解答 】 (1) 连接 OD,OF, ∵⊙O 是△ ABC 的内切圆 , ∴OD⊥AB,OF⊥AC. ∵∠DOF=2∠DEF=2×45°=90°, ∴ 四边形 ADOF 是矩形 , ∴∠A=90°. (2) 设⊙ O 的半径为 r, 由 (1) 知四边形 ADOF 是矩形 , 又 OD=OF, ∴ 四边形 ADOF 是正方形 . ∴OD∥AC. ∴△BOD∽△BGA. 即 解得 ∴⊙ O 的半径为 【 总结提升 】 三角形的内切圆 1. 在解决三角形内切圆的相关问题时 , 常利用切线性质 , 借助方 程、方程组模型加以解决或利用内心性质来判定切线 . 2. 三角形内切圆的半径与三角形面积的关系：三角形的面积为 在有些计算三角形内切圆的半径时 , 可通过勾 股定理把三角形的面积求出来 ,a,b,c 三边已知 , 代入上式可求 出内切圆的半径 . 题组一： 切线的判定 1. 下列说法正确的是 ( ) A. 圆的切线必垂直于半径 B. 垂直于切线的直线必经过圆心 C. 垂直于切线的直线必经过切点 D. 经过圆心与切点的直线必垂直于切线 【 解析 】 选 D. 圆的切线必垂直于经过切点的半径，故 A 项错误；垂直于切线的直线有无数条，不一定过圆心，垂直于切线的直径才过圆心和切点，故选项 B ， C 错误； D 正确 . 2. 如图，△ ABC 的一边 AB 是⊙ O 的直径，请你添加一个条件，使 BC 是⊙ O 的切线，你所添加的条件为 ______ ． 【 解析 】 当△ ABC 为直角三角形时，即∠ ABC ＝ 90° 时， BC 与圆相切，∵ AB 是⊙ O 的直径，∠ ABC ＝ 90° ，∴ BC 是⊙ O 的切线 . 答案： ∠ ABC ＝ 90 ° ( 答案不惟一 ) 3. 如图 , 点 A,B,D 在⊙ O 上 ,∠A=25°,OD 的延长线交直线 BC 于点 C, 且∠ OCB=40°, 直线 BC 与⊙ O 的位置关系为 _______. 【 解析 】 ∵∠BOC=2∠A=50°,∠OCB=40°,∴ 在△ OBC 中 ,∠OBC=180°-50°-40°=90°.∴ 直线 BC 与⊙ O 相切 . 答案： 相切 4.(2013· 滨州中考 ) 如图，在△ ABC 中， AB=AC ，点 O 在边 AB 上，⊙ O 过点 B 且分别与边 AB ， BC 相交于点 D ， E ， EF⊥AC ，垂足为 F ．求证：直线 EF 是⊙ O 的切线． 【 证明 】 连接 OE ，∵ OB=OE ，∴∠ B=∠OEB ． ∵ AB=AC ，∴∠ B=∠C ．∴∠ OEB=∠C ．∴ OE∥AC ． ∵ EF ⊥ AC ，∴ OE ⊥ EF ．∴直线 EF 是⊙ O 的切线． 5.(2013· 珠海中考 ) 如图，⊙ O 经过菱形 ABCD 的三个顶点 A ， C ， D ，且与 AB 相切于点 A ， (1) 求证： BC 为⊙ O 的切线 . (2) 求∠ B 的度数 . 【 解析 】 (1) 连接 OA ， OB ， OC,∵ AB 切⊙ O 于点 A, ∴∠BAO=90°,∵ 四边形 ABCD 是菱形 ,∴BA=BC, ∵OA=OC,OB=OB,∴△ABO≌△CBO(SSS), ∴∠BCO=∠BAO=90°, ∴BC 为⊙ O 的切线 . (2)∵∠AOC=2∠D, ∠B=∠D, ∴ ∠AOC=2∠B, 又∵∠ AOC+∠B=180°, ∴∠B=60°. 题组二： 三角形的内切圆 1. 下列命题正确的是 ( ) A. 三角形的内心到三角形三个顶点的距离相等 B. 三角形的内心不一定在三角形的内部 C. 等边三角形的内心、外心重合 D. 一个圆一定有惟一的一个外切三角形 【 解析 】 选 C. 三角形的内心是三角形三个内角平分线的交点，所以到三角形三边的距离相等，三角形的内心一定在三角形内部，等边三角形的三边垂直平分线的交点与角平分线的交点重合 ; 一个圆有无数个外切三角形，故选 C. 2. 如图所示，点 O 为△ ABC 的内切圆的圆心，若∠ BAC=80° ，则∠ BOC 的度数为 ( ) A.130° B.100° C.50° D.65° 【 解析 】 选 A. ∵ 点 O 是△ ABC 的内心， ∴∠ BOC=180°-(∠OBC+∠OCB) 【 归纳整合 】 直角三角形内切圆的半径的两种求法 已知直角三角形直角边为 a,b ，斜边为 c ，直角三角形内切圆半 径为 r. (1) 切线长定理：根据切线长定理推得 ,a-r+b-r=c ， 即 (2) 面积法：根据三角形面积等于三角形的周长与三角形内切 圆半径乘积的一半，得 即 3. 如图，在等腰直角三角形 ABC 中， AB ＝ AC ＝ 8 ， O 为 BC 的中点，以 O 为圆 心作半圆，使它与 AB ， AC 都相切， 切点分别为 D ， E ，则⊙ O 的半径为 ( ) A.8 B.6 C.5 D.4 【 解析 】 选 D. 连接 OD ，则 OD⊥AB ，∠ A ＝ 90° ，∴ OD∥AC ， ∴△ BOD∽△BCA ， 又∵ O 为 BC 的中点，∴ OD ＝ 则 OD ＝ 4 ，⊙ O 的半径为 4 ． 4. 如图 , 正三角形 ABC 的内切圆半径为 1, 那么三角形的边长为 ______. 【 解析 】 过 O 点作 OD⊥AB 于 D, 则 OD=1,∵O 是△ ABC 的内心 , ∴∠OAD=30°. 在 Rt△OAD 中 ,∠OAD=30°,OD=1, 答案： 5. 如图，⊙ O 是四边形 ABCD 的内切圆， E ， F ， G ， H 是切点，点 P 是 上异于 E ， H 的点 . 若∠ A ＝ 50° ，则∠ EPH ＝ _____. 【 解析 】 连接 OH ， OE ， ∵⊙ O 是四边形 ABCD 的内切圆，∴ OH⊥AD ， OE⊥AB ，∵∠ A ＝ 50° ，∴∠ HOE ＝ 130° ， 答案： 65 ° 【 想一想错在哪？ 】 已知 OC 平分∠ AOB ， D 是 OC 上任意一点，⊙ D 与 OA 相切于点 E ，求证： OB 与⊙ D 相切 . 提示： 证明 OB 为⊙ D 的切线，尚不知道 OB 与⊙ D 是否有公共点，所以不能 “ 连半径，判垂直 ” ，而应该 “ 作垂直，判半径 ” .