北师大版九年级数学（下册）第一章直角三角形的边角关系

北师大版九年级数学（下册）第一章直角三角形的边角关系

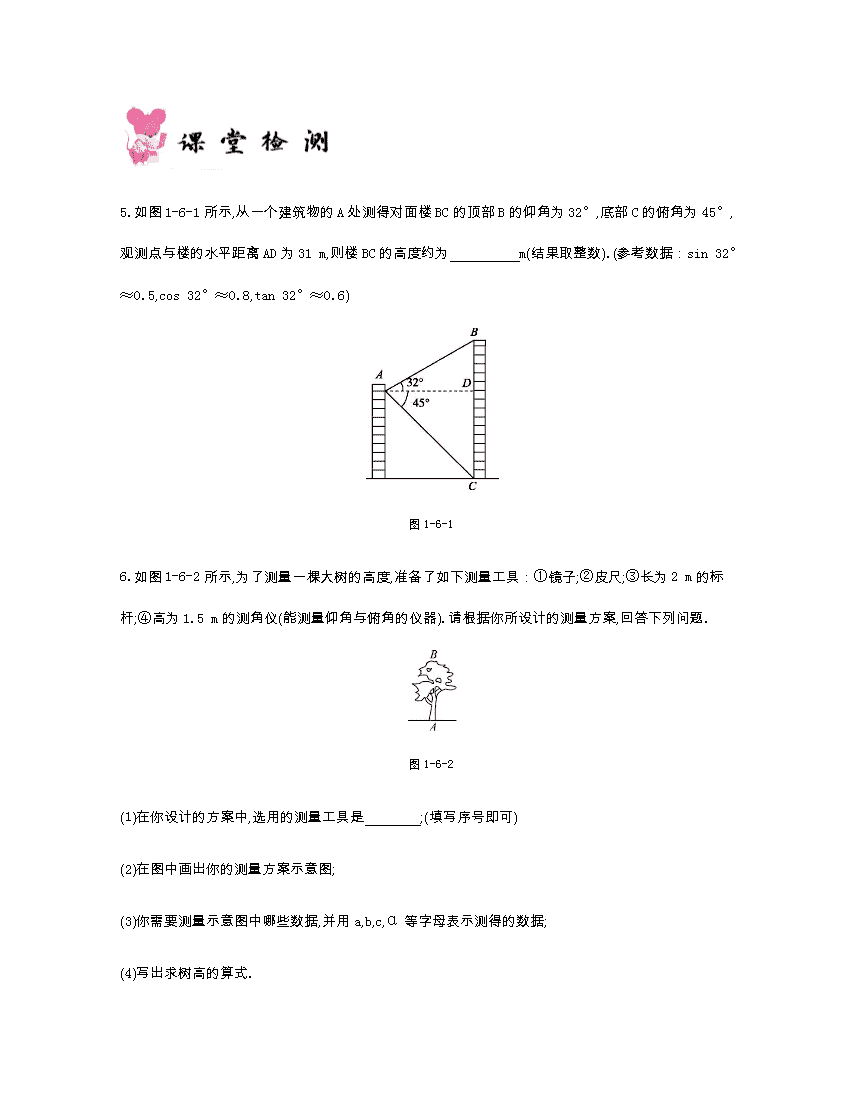
北师大版九年级数学（下册）‎ 第一章 直角三角形的边角关系 ‎1.6利用三角函数测高 课时练习 ‎1.简单的测倾器由　　　　　、　　　　　和　　　　　组成. ‎ ‎2.所谓“底部可以到达”是指：　　　　　　　　　　　　　　　　　　　　.‎ ‎3.所谓“底部不可以到达”是指：　　　　　　　　　　　　　　　　　　　　. ‎ ‎4.使用测倾器测量倾斜角的步骤为(　　)‎ ‎①记下此时铅垂线所指的度数;‎ ‎②使支杆的中心线、铅垂线和度盘的0°刻度线重合;‎ ‎③转动度盘,使度盘的直径对准目标M;‎ ‎④使度盘的顶线在水平位置;‎ ‎⑤把支杆竖直插入地面.‎ A.①②③④⑤‎ B.⑤④③②①‎ C.⑤②④③①‎ D.③⑤②④①‎ ‎5.如图1-6-1所示,从一个建筑物的A处测得对面楼BC的顶部B的仰角为32°,底部C的俯角为45°,观测点与楼的水平距离AD为31 m,则楼BC的高度约为　　　　　m(结果取整数).(参考数据：sin 32°≈0.5,cos 32°≈0.8,tan 32°≈0.6) ‎ 图1-6-1‎ ‎6.如图1-6-2所示,为了测量一棵大树的高度,准备了如下测量工具：①镜子;②皮尺;③长为2 m的标杆;④高为1.5 m的测角仪(能测量仰角与俯角的仪器).请根据你所设计的测量方案,回答下列问题.‎ 图1-6-2‎ ‎(1)在你设计的方案中,选用的测量工具是　　　　;(填写序号即可) ‎ ‎(2)在图中画出你的测量方案示意图;‎ ‎(3)你需要测量示意图中哪些数据,并用a,b,c,α等字母表示测得的数据;‎ ‎(4)写出求树高的算式.‎ ‎7.如图1-6-3所示,河对岸有高层建筑物AB,为测量其高,在C处由点D用测倾器测得顶端A的仰角为30°,向高层建筑物前进50 m,到达C’处,由点D’测得顶端A的仰角为45°,已知测倾CD=C’D’=1.2 m ,则高层建筑物AB的高为　　　　　.(取1.732)‎ 图1-6-3‎ ‎8.学习完解直角三角形的有关知识后,老师布置一道利用测倾器测量学校旗杆高度的实习作业,下表是小明同学制作的实习报告,请你根据有关测量数据,求旗杆高AB.‎ 实习报告 题目 测量底部可以到达的旗杆高 测量 目标 测得 数据 BD的长 BD=20.00 m 测倾器的高 CD=1.21 m 倾斜角 α=28°‎ 计算 旗杆高AB的计算过程(精确到0.1 m)‎ ‎9.合肥新桥国际机场出港大厅有一幅“黄山胜景”的壁画.聪聪站在距壁画水平距离15米的地面,自A点看壁画上部D的仰角为45°,看壁画下部C的仰角为30°,求壁画CD的高度.(参考数据：≈1.7,≈1.4,精确到0.1)‎ 图1-6-4‎ ‎10.如图1-6-5所示,AC表示一幢楼,它的各楼层都可到达;BD表示一个建筑物,且上面不能到达.已知AC与BD地平高度相同,AC周围没有开阔地带,仅有的测量工具有皮尺(可测量长度)和测倾器(可测量仰角、俯角和两视线间的夹角).‎ 图1-6-5‎ ‎(1)请你设计一个测量建筑物BD高度的方案,要求写出测量步骤和必要的测量数据(用字母表示),并画出测量示意图;‎ ‎(2)写出计算BD高度的表达式.‎ 参考答案 ‎1.度盘、铅锤、支杆 ‎2.在地面上可以无障碍地直接测得测点与被测物体的底部之间的距离 ‎3.在地面上不能直接测得测点与被测物体的底部之间的距离 ‎4.C ‎5.50‎ ‎6.解：(1)②④.‎ ‎(2)测量方案如图所示：‎ ‎(3)测角仪离树的底部的距离CA=a m,‎ 测角仪的顶端到树的顶端的仰角∠BDE=α.‎ ‎(4)树的高度AB=(1.5+a tan α)m.‎ ‎7.69.5 m ‎8.解：在矩形BECD中,‎ CE=BD=20.00 m,BE=CD=1.21 m.‎ 在Rt△AEC中,‎ AE=CE· tan α=20.00×tan 28°≈10.63(m).‎ 所以AB=AE+BE≈10.63+1.21≈11.8(m).‎ ‎9.解：过A点作AB⊥DC于点B,则AB=15,‎ 在Rt△ABD中,∠DAB=45°,‎ ‎∴BD=AB=15.‎ 在Rt△ABC中,∠BAC=30°,‎ ‎∴BC=AB·tan 30°=15×=5.‎ ‎∴CD=BD-BC=15-5≈15-5×1.7=6.5.‎ 答：壁画CD的高度约为6.5米.‎ ‎10.略