沪科版九年级数学上册期末测试题2（含答案）

沪科版九年级数学上册期末测试题2（含答案）

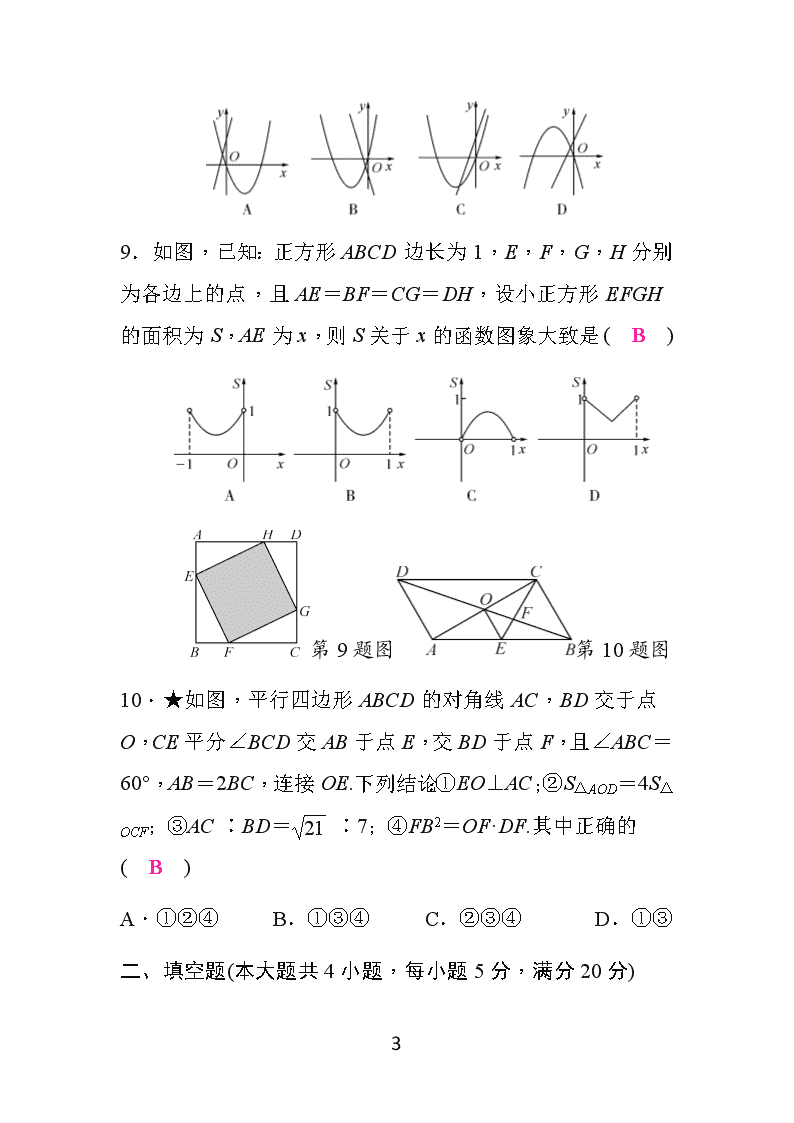
沪科版九年级数学上册期末测试题2（含答案）‎ ‎(考试时间：120分钟　　　满分：150分)‎ 姓名：______　　　班级：______　　　分数：______‎ 一、选择题(本大题共10小题，每小题4分，满分40分)‎ 每小题都给出A、B、C、D四个选项，其中只有一个是正确的．‎ ‎1．cos 45°的值等于 (　D　)‎ A. B. C. D. ‎2．将抛物线y＝x2向右平移2个单位长度，再向上平移3个单位长度后，抛物线的表达式为 (　B　)‎ A．y＝(x＋2)2＋3 B．y＝(x－2)2＋3‎ C．y＝(x＋2)2－3 D．y＝(x－2)2－3‎ ‎3．反比例函数y＝－(x＞0)的图象位于 (　D　)‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎4．如图，点P在反比例函数y＝(k≠0)的图象上，PA⊥x轴于点A，△PAO的面积为2，则k的值为 (　C　)‎ A．1 B．2 C．4 D．6‎ 13‎ 第4题图 第7题图 ‎5．在△ABC中，∠C＝90°，a，b，c分别为∠A，∠B，∠C的对边，下列各式成立的是 (　D　)‎ A．sin B＝ B．cos B＝ C．tan B＝ D．tan B＝ ‎6．点C是线段AB的黄金分割点(AC＞BC)，且AB＝6 cm，则BC的长为 (　A　)‎ A．(9－3)cm B．(9＋3)cm C．(3－3)cm D．(6－6)cm ‎7．如图，已知在△ABC中，P为AB上一点，连接CP，以下条件中不能判定△ACP∽△ABC的是 (　C　)‎ A．∠ACP＝∠B B．∠APC＝∠ACB C.＝ D.＝ ‎8．在同一平面直角坐标系中，函数y＝2x2＋k x与y＝k x＋k(k≠0)的图象大致是 (　C　)‎ 13‎ ‎ ‎ ‎9．如图，已知：正方形ABCD边长为1，E，F，G，H分别为各边上的点，且AE＝BF＝CG＝DH，设小正方形EFGH的面积为S，AE为x，则S关于x的函数图象大致是(　B　)‎ ‎ ‎ 第9题图第10题图 ‎10．★如图，平行四边形ABCD的对角线AC，BD交于点O，CE平分∠BCD交AB于点E，交BD于点F，且∠ABC＝60°，AB＝2BC，连接OE.下列结论：①EO⊥AC；②S△AOD＝4S△OCF；③AC ∶BD＝ ∶7；④FB2＝OF·DF.其中正确的(　B　)‎ A．①②④ B．①③④ C．②③④ D．①③‎ 二、填空题(本大题共4小题，每小题5分，满分20分)‎ 13‎ ‎11．若＝，且a－b＝－2，则a＋b的值是 12 .‎ ‎12．如图，传送带把物体从地面送到离地面5米高的地方，如果传送带与地面所成的斜坡的坡度i＝1 ∶2.4，那么物体所经过的路程AB为 13 米．‎ 第12题图第13题图 ‎13．已知二次函数y＝ax2＋bx＋c与一次函数y＝x的图象如图所示，则不等式ax2＋(b－1)x＋c＜0的解集为 1＜x＜3 .‎ ‎14．在△ABC中，∠C＝90°，AC＝4，BC＝3，D是边AB上一点，E是边AC上的一点(D，E与端点不重合)，如果△CDE与△ABC相似，那么CD的长是 或 .‎ 三、(本大题共2小题，每小题8分，满分16分)‎ ‎15．计算：2cos 45°－tan 60°＋sin 30°－.‎ 解：原式＝2×－＋－ ‎＝－.‎ 13‎ ‎16．如图，△ABC的三个顶点坐标分别是A(0，3)，B(1，0)，C(3，1)．‎ ‎(1)以原点O为位似中心，在y轴左侧画出△A1B1C1，使得△A1B1C1与△ABC的位似比为2 ∶1；‎ ‎(2)△ABC的内部一点M的坐标为(a，b)，则点M在△A1B1C1中的对应点M1的坐标是多少？‎ ‎ ‎ 解：(1)如图所示，△A1B1C1即为所求．‎ ‎(2)△ABC的内部一点M的坐标为(a，b)，则点M在△A1B1C1中的对应点M1的坐标是(－2a，－2b)．‎ 四、(本大题共2小题，每小题8分，满分16分)‎ ‎17．如图，在等边三角形ABC中，点D，E分别在BC，AB上，且∠ADE＝60°.求证：△ADC∽△DEB.‎ ‎ ‎ 13‎ 证明：∵△ABC是等边三角形，‎ ‎∴∠B＝∠C＝60°，‎ ‎∴∠ADB＝∠CAD＋∠C＝∠CAD＋60°，‎ ‎∵∠ADE＝60°，∴∠ADB＝∠BDE＋60°，‎ ‎∴∠CAD＝∠BDE，∴△ADC∽△DEB.‎ ‎18．若二次函数图象经过点A(－1，0)，B(3，0)，C(0，5)三点，求该二次函数表达式．‎ 解：设二次函数表达式为y＝a(x＋1)(x－3)，‎ 把(0，5)代入得－3a＝5，‎ 解得a＝－，‎ 则二次函数表达式为y＝－(x＋1)(x－3)＝－x2＋x＋5‎ 五、(本大题共2小题，每小题10分，满分20分)‎ ‎19．某商场为缓解某市“停车难”问题，拟建造地下停车库，如图是该地下停车库坡道入口的设计示意图，其中，AB⊥BD，∠BAD＝18°，C在BD上，BC＝0.5 m．根据规定，地下停车库坡道入口上方要张贴限高标志，以便告知驾驶员所驾车辆能否安全驶入．小明认为CD的长就是所限制的高度，‎ 13‎ 而小亮认为应该以CE的长作为限制的高度．小明和小亮谁说的对？请你判断并计算出正确的结果．(参考数据：sin 18°＝0.31，cos 18°＝0.95，tan 18°＝0.325)(结果精确到0.1 m)‎ ‎ ‎ 解：在△ABD中，∠ABD＝90°，∠BAD＝18°，BA＝10 m，‎ ‎∵tan∠BAD＝，‎ ‎∴BD＝10×tan 18°，‎ ‎∴CD＝BD－BC ‎＝10×tan 18°－0.5‎ ‎＝2.75 m. ‎ 在△ABD中，∠CDE＝90°－∠BAD＝72°，‎ ‎∵CE⊥ED，∴sin∠CDE＝，‎ ‎∴CE＝sin∠CDE×CD ‎＝sin 72°×2.75‎ ‎＝cos 18°×2.75＝0.95×2.75＝2.612 5≈2.6 m，‎ ‎∵2.6 m＜2.75 m，且CE⊥AE，∴小亮说的对．‎ 答：小亮说的对，CE的长为2.6 m.‎ 13‎ ‎20．如图，已知A(－4，2)，B(n，－4)是一次函数y＝k x＋b的图象与反比例函数y＝(m≠0)的图象的两个交点．‎ ‎(1)求反比例函数和一次函数的表达式；‎ ‎(2)根据图象写出使一次函数的函数值小于反比例函数的函数值的x的取值范围．‎ ‎ ‎ 解：(1)把A(－4，2)代入y＝得m＝－8，则反比例函数的表达式是y＝－；‎ 把y＝－4代入y＝－，得x＝n＝2，‎ 则B的坐标是(2，－4)．‎ 根据题意得解得 则一次函数的表达式是y＝－x－2.‎ ‎(2)由图象可知，使一次函数的函数值小于反比例函数的函数值的x的取值范围是－4＜x＜0或x＞2.‎ 13‎ 六、(本题满分12分)‎ ‎21．某公司投入研发费用80万元(80万元只计入第一年成本)，成功研发出一种产品．公司按订单生产(产量＝销售量)，第一年该产品正式投产后，生产成本为6元/件，此产品年销售量y(万件)与售价x(元/件)之间满足一次函数关系，其函数图象如图所示．‎ ‎(1)求y与x之间的函数关系式；‎ ‎(2)该产品第一年的利润为20万元，那么该产品第一年的售价是多少？‎ ‎(3)第二年，该公司将第一年的利润20万元再次投入研发(20万元只计入第二年成本)，以降低产品的生产成本，预计第二年的年销售量与售价仍存在(1)中的函数关系．为保持市场占有率，公司规定第二年产品售价为14元/件，若想实现第二年利润不低于88万元的目标，该产品的生产成本单价应控制在不超过多少元？‎ ‎ ‎ 解：(1)y与x之间的函数关系式y＝－x＋26.‎ 13‎ ‎(2)根据题意(x－6)(－x＋26)－80＝20，解得x＝16，‎ 故该产品第一年的售价是16元．‎ ‎(3)设若想实现第二年利润不低于88万元的目标，该产品的生产成本单价应控制在不超过a元．‎ 根据题意，当售价为14元时，销售量为－14＋26＝12万件，‎ ‎12(14－a)－20≥88，解得a≤5，‎ 故若想实现第二年利润不低于88万元的目标，该产品的生产成本单价应控制在不超过5元．‎ 七、(本题满分12分)‎ ‎22．如图，平行四边形ABCD中，∠B＝30°，过点A作AE⊥BC于点E，现将△ABE沿直线AE翻折至△AFE的位置，AF与CD交于点G.‎ ‎(1)求证：CG·BF＝CD·CF；‎ ‎(2)若AB＝4，AD＝8，求DG的长．‎ ‎(1)证明：∵在平行四边形ABCD中，‎ AB＝CD，AB∥DC，‎ 13‎ ‎∴△CGF∽△BAF，∴＝，‎ ‎∴＝，∴CG·BF＝CD·CF.‎ ‎(2)解：∵∠B＝30°，AE⊥BC，AB＝4，‎ ‎∴AE＝AB＝2，∴BE＝＝＝6，‎ ‎∵△ABE沿直线AE翻折至△AFE的位置，∴EF＝BE＝6，‎ ‎∴BF＝12，∵在平行四边形ABCD中，AD＝BC，AB＝CD，且AD＝8，‎ AB＝4，∴BC＝8，CD＝4，∴CF＝BF－BC＝12－8＝4，‎ ‎∵＝，∴＝，∴CG＝，‎ ‎∴DG＝CD－CG＝4－＝.‎ 八、(本题满分14分)‎ ‎23．定义：由两条与x轴有着相同的交点，并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”．如图，抛物线C1与抛物线C2组成一个开口向上的“月牙线”，抛物线C1与抛物线C2与x轴有相同的交点M，N(点M在点N的左侧)，与y轴的交点分别为A，B且点A的坐标为(0，－3)，‎ 13‎ 抛物线C2的表达式为y＝mx2＋4mx－12m(m＞0)．‎ ‎(1)请你根据“月牙线”的定义，设计一个开口向下的“月牙线”，直接写出两条抛物线的表达式；‎ ‎(2)求M，N两点的坐标；‎ ‎(3)在第三象限内的抛物线C1上是否存在一点P，使得△PAM的面积最大？若存在，求出△PAM的面积的最大值；若不存在，说明理由．‎ 题图答图 解：(1)如图①，抛物线y＝－x2＋2x＋3与抛物线y＝－x2＋x＋1所围成的封闭曲线即为开口向下的“月牙线”．‎ ‎(2)在抛物线C2的表达式y＝mx2＋4mx－12m中，‎ 当y＝0时，mx2＋4mx－12m＝0，‎ ‎∵m≠0，∴x2＋4x－12＝0，解得x1＝－6，x2＝2，‎ ‎∵点M在点N的左边，∴M(－6，0)，N(2，0)．‎ ‎(3)在第三象限内的抛物线C1上存在一点P，使得△PAM的面积最大．如图②，连接AM，PO，PM，PA，‎ 13‎ ‎∵抛物线C1和抛物线C2与x轴有着相同的交点，并且开口方向相同，∴可设抛物线C1的表达式y＝nx2＋4nx－12n(n＞0)，‎ ‎∵抛物线C1与y轴的交点为A(0，－3)，∴－12n＝－3，∴n＝，‎ ‎∴抛物线C1的表达式为y＝x2＋x－3，‎ ‎∴可设点P的坐标为，‎ ‎∴S△PAM＝S△PMO＋S△PAO－S△AOM ‎＝×6×＋×3×(－t)－×6×3‎ ‎＝－t2－t＝－(t＋3)2＋，‎ ‎∵－＜0，－6＜t＜0，‎ ‎∴根据二次函数的图象和性质知，当t＝－3时，即点P的坐标为时，△PAM的面积有最大值，最大值为.‎ 13‎