- 2021-11-11 发布 |
- 37.5 KB |
- 30页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
福建专版2020中考数学复习方案第七单元视图与变换第34课时尺规作图课件
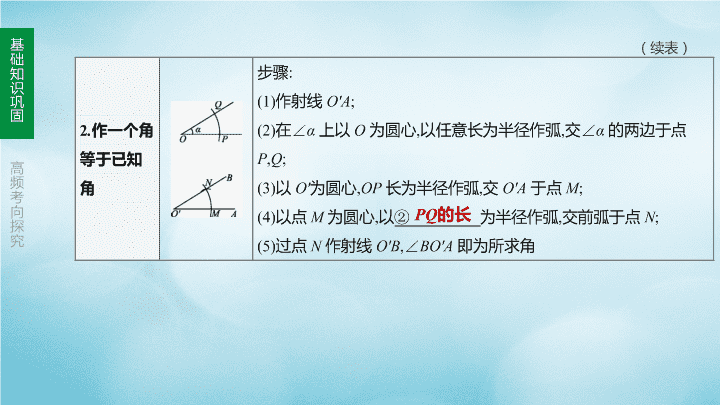
第 34 课时 尺规作图 第七单元 视图与变换 基 础 知 识 巩 固 高 频 考 向 探 究 考点 五种基本尺规作图 考点聚焦 OA=a 基 础 知 识 巩 固 高 频 考 向 探 究 (续表) PQ的长 基 础 知 识 巩 固 高 频 考 向 探 究 (续表) 基 础 知 识 巩 固 高 频 考 向 探 究 (续表) 基 础 知 识 巩 固 高 频 考 向 探 究 题组一 必会题 对点演练 图34-1 基 础 知 识 巩 固 高 频 考 向 探 究 [答案]B [解析]在△ABC中,∵∠B=30°,∠C=90°, ∴∠BAC=180°-∠B-∠C=60°, 由作图可知MN为AB的垂直平分线,∴DA=DB, ∴∠DAB=∠B=30°, ∴∠CAD=∠BAC-∠DAB=30°, 故选B. 基 础 知 识 巩 固 高 频 考 向 探 究 解:如图,四边形ABCD即为所求. 2.[2019·南平八校联考]已知:∠MAN和线段a. 求作:菱形ABCD,使顶点B,D分别在射线AM,AN上,且对角线AC=a. 图34-2 基 础 知 识 巩 固 高 频 考 向 探 究 3.[2019·青岛]已知:∠α,直线l及l上两点A,B. 求作:Rt△ABC,使点C在直线l的上方,且∠ABC=90°,∠BAC=∠α. 图34-3 解:如图,Rt△ABC为所求. 基 础 知 识 巩 固 高 频 考 向 探 究 4.如图34-4,已知Rt△ABC,∠C=90°. (1)用尺规作图法在线段AC上求作一点D,使得D到AB的距离等于DC(不写作法, 保留作图痕迹); (2)若AB=10,CD=3,求△ABD的面积. 图34-4 解:(1)如图所示,点D即为所求. 基 础 知 识 巩 固 高 频 考 向 探 究 4.如图34-4,已知Rt△ABC,∠C=90°. (2)若AB=10,CD=3,求△ABD的面积. 图34-4 基 础 知 识 巩 固 高 频 考 向 探 究 解:(1)如图,∠ADE为所作. 5.如图34-5,在△ABC中,AB>AC,点D在边AC上. (1)作∠ADE,使∠ADE=∠ACB,DE交AB于点E;(尺规作图,保留作图痕迹,不写作法) (2)若BC=5,点D是AC的中点,求DE的长. 图34-5 基 础 知 识 巩 固 高 频 考 向 探 究 5.如图34-5,在△ABC中,AB>AC,点D在边AC上. (2)若BC=5,点D是AC的中点,求DE的长. 图34-5 基 础 知 识 巩 固 高 频 考 向 探 究 6.[2019·泉州模拟](1)如图34-6,已知线段a和∠MBN,请在给出的图形上用尺规作 图法作出△ABC,使得点A在射线BN上,点C在射线BM上,且AB=a,∠ACB=90°;(保 留作图痕迹,不写作法) (2)求证:直角三角形斜边上的中线等于斜边的一半.(要求:利用(1)中的Rt△ABC, 画出斜边AB上的中线CD,写出已知、求证和证明过程) 图34-6 解:(1)如图,△ABC为所作图形. 基 础 知 识 巩 固 高 频 考 向 探 究 6.[2019·泉州模拟](2)求证:直角三角形斜边上的中线等于斜边的一半.(要求:利 用(1)中的Rt△ABC,画出斜边AB上的中线CD,写出已知、求证和证明过程) 图34-6 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 题组二 易错题 【失分点】 不能确定使用哪一个基本作图类型来完成复杂作图;尺规作图时不按规范的作 图步骤进行,导致结果不同;不能根据作图痕迹判断出作图结论. 基 础 知 识 巩 固 高 频 考 向 探 究 D 7.[2018·河北] 尺规作图要求:Ⅰ.过直线外一点作这条直线的垂线;Ⅱ.作线段的垂直 平分线;Ⅲ.过直线上一点作这条直线的垂线;Ⅳ.作角的平分线. 图34-7是按上述要求排乱顺序的尺规作图: 则正确的配对是 ( ) A.①—Ⅳ,②—Ⅱ,③—Ⅰ,④—Ⅲ B.①—Ⅳ,②—Ⅲ,③—Ⅱ,④—Ⅰ C.①—Ⅱ,②—Ⅳ,③—Ⅲ,④—Ⅰ D.①—Ⅳ,②—Ⅰ,③—Ⅱ,④—Ⅲ 图34-7 基 础 知 识 巩 固 高 频 考 向 探 究 C8.[2019·河北]根据圆规作图的痕迹,可用直尺成功找到三角形外心的是 ( ) 图34-8 基 础 知 识 巩 固 高 频 考 向 探 究 考向一 判断作图结论 [答案] B [解析]∵∠ADC=2∠B,且 ∠ADC=∠B+∠BCD, ∴∠B=∠BCD,∴DC=DB, ∴点D在线段BC的垂直平分线 上,故选B. 例1 [2019·长春]如图34-9,在△ABC中,∠ACB为 钝角.用直尺和圆规在边AB上确定一点D,使 ∠ADC=2∠B,则符合要求的作图痕迹是( ) 图34-9 基 础 知 识 巩 固 高 频 考 向 探 究 考向二 结合几何知识的综合题 例2[2019·厦门质检]如图34-10,在正方形ABCD中,E是CD边上的点,过点E作 EF⊥BD于F. (1)尺规作图:在图中求作点E,使得EF=EC; (保留作图痕迹,不写作法) (2)在(1)的条件下连接FC,求∠BCF的度数. 图34-10 解:(1)如图所示,E为所求作的点. 基 础 知 识 巩 固 高 频 考 向 探 究 例2[2019·厦门质检]如图34-10,在正方形ABCD中,E是CD边上的点,过点E作 EF⊥BD于F. (2)在(1)的条件下连接FC,求∠BCF的度数. 图34-10 基 础 知 识 巩 固 高 频 考 向 探 究 | 考向精练 | 图34-11 1.[2017·福建19题]如图34-11,△ABC中,∠BAC=90°,AD⊥BC,垂足为D.求作∠ABC 的平分线,分别交AD,AC于P,Q两点,并证明AP=AQ.(要求:尺规作图,保留作图痕 迹,不写作法) 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2019·福建20题]已知△ABC和点A',如图34-12. (1)以点A'为一个顶点作△A'B'C',使得△A'B'C'∽△ABC,且△A'B'C'的面积等于△ABC 面积的4倍;(要求:尺规作图,不写作法,保留作图痕迹) (2)设D,E,F分别是△ABC三边AB,BC,CA的中点,D',E',F'分别是你所作的△A'B'C'三 边A'B',B'C',C'A'的中点,求证:△DEF∽△D'E'F'. 图34-12 解:(1)如图:△A'B'C'为所求作图形. 基 础 知 识 巩 固 高 频 考 向 探 究 2.[2019·福建20题]已知△ABC和点A',如图34-12. (2)设D,E,F分别是△ABC三边AB,BC,CA的中点,D',E',F'分别是你所作的△A'B'C'三 边A'B',B'C',C'A'的中点,求证:△DEF∽△D'E'F'. 图34-12 基 础 知 识 巩 固 高 频 考 向 探 究 基 础 知 识 巩 固 高 频 考 向 探 究 考向三 探究及综合类问题 例3[2019·福州适应性练习]我们把有两边对应相等,且夹角互补(不相等)的两个 三角形叫做“互补三角形”,如图34-13①,▱ ABCD中,△AOB和△BOC是“互补三角 形”. (1)写出图①中另外一组“互补三角形”___________________________________ ; (2)在图②中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH 和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等. 图34-13 答案不唯一,如:△AOD和△AOB,△AOD和 △DOC等 基 础 知 识 巩 固 高 频 考 向 探 究 例3[2019·福州适应性练习]我们把有两边对应相等,且夹角互补(不相等)的两个三 角形叫做“互补三角形”,如图34-13①,▱ ABCD中,△AOB和△BOC是“互补三角形”. (2)在图②中,用尺规作出一个△EFH,使得△EFH和△EFG为“互补三角形”,且△EFH 和△EFG在EF同侧,并证明这一组“互补三角形”的面积相等. 图34-13 基 础 知 识 巩 固 高 频 考 向 探 究 (2)如图所示,△EFH为所求作的三角形, 作GP⊥EF于P,HQ⊥EF交EF延长线于Q. ∵GH=EF,FH=EG, ∴四边形EFHG是平行四边形, ∴GH∥EF,GP=HQ,△EFH和△EFG同底等高, ∴三角形面积相等.查看更多