2010中考数学本溪考试试题

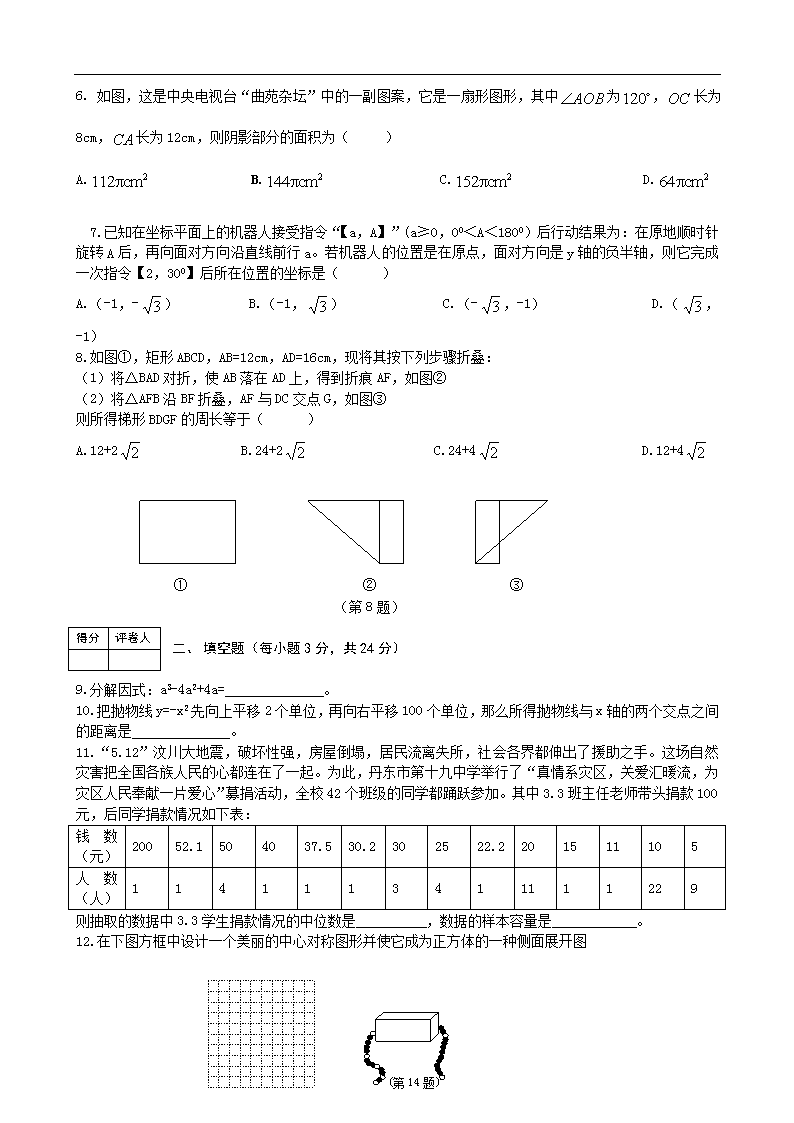
2010中考数学本溪考试试题

‎2010年本溪中考数学试卷 ‎※答卷时间：120分钟 满分值：150分 题号 一 二 三 四 五 六 七 八 总分 得分 得分 评卷人 ‎ ‎ 一、 选择题（下列各题的备选答案中，只有一个是正确的，将正确答案的序号填在题后括号内，每小题3分，共24分）‎ ‎1.从今年6月1日起，在我国各大超市、市场实行塑料购物袋有偿使用制度，这一措施有利于控制白色污染。已知一个塑料袋丢弃在地上的面积为500cm2，如果100万名游客每人丢弃一个塑料袋，那么会污染的最大面积用科学计数法表示是（ ）‎ A.5×104m2 B. 5×106m2 C. 5×103m2 D. 5×10-2m2‎ ‎2.已知一次函数y=(a-2)x+b的图像如图所示，那么a的取值范围是（ ）‎ A.a<2 B.a>2 C.a<0 D.a>0‎ A C O B ‎（第6题）‎ ‎ Y ‎（第2题） （第5题）‎ ‎3. 某展厅内要用相同的正方体木块搭成一个三视图如下的展台,则此展台至少需这样的正方体 （ ）‎ A.4块 B.5块 C.6块 D.7块 ‎4.为执行“两免一补”政策，丹东地区2007年投入教育经费2500万元，预计2009年投入3600万元，则这两年投入教育经费的平均增长率为 （ ）‎ A.10% B.20% C.30% D.15%‎ ‎5.如图，△ABC是⊙O的内接三角形，AD⊥BC于D点，且AC=5,CD=3,AB=4，则⊙O的直径等于 （ ）‎ A. B.3 C.5 D.7‎ ‎6. 如图，这是中央电视台“曲苑杂坛”中的一副图案，它是一扇形图形，其中为，长为8cm，长为12cm，则阴影部分的面积为（ ）‎ A. B. C. D. ‎ ‎7.已知在坐标平面上的机器人接受指令“【a，A】”(a≥0，00＜A＜1800）后行动结果为：在原地顺时针旋转A后，再向面对方向沿直线前行a。若机器人的位置是在原点，面对方向是y轴的负半轴，则它完成一次指令【2，300】后所在位置的坐标是（ ）‎ A.（-1，-） B.（-1，） C.（-，-1） D.（，-1）‎ ‎8.如图①，矩形ABCD，AB=12cm，AD=16cm，现将其按下列步骤折叠：‎ ‎（1）将△BAD对折，使AB落在AD上，得到折痕AF，如图②‎ ‎（2）将△AFB沿BF折叠，AF与DC交点G，如图③‎ 则所得梯形BDGF的周长等于（ ）‎ A.12+2 B.24+2 C.24+4 D.12+4‎ ‎ ① ② ③ ‎ ‎（第8题）‎ 得分 评卷人 ‎ ‎ 一、 填空题（每小题3分，共24分）‎ ‎9.分解因式：a3-4a2+4a= 。‎ ‎10.把抛物线y=-x2先向上平移2个单位，再向右平移100个单位，那么所得抛物线与x轴的两个交点之间的距离是 。‎ ‎11.“5.12”汶川大地震，破坏性强，房屋倒塌，居民流离失所，社会各界都伸出了援助之手。这场自然灾害把全国各族人民的心都连在了一起。为此，丹东市第十九中学举行了“真情系灾区，关爱汇暖流，为灾区人民奉献一片爱心”募捐活动，全校42个班级的同学都踊跃参加。其中3.3班主任老师带头捐款100元，后同学捐款情况如下表：‎ 钱数（元）‎ ‎200‎ ‎52.1‎ ‎50‎ ‎40‎ ‎37.5‎ ‎30.2‎ ‎30‎ ‎25‎ ‎22.2‎ ‎20‎ ‎15‎ ‎11‎ ‎10‎ ‎5‎ 人数（人）‎ ‎1‎ ‎1‎ ‎4‎ ‎1‎ ‎1‎ ‎1‎ ‎3‎ ‎4‎ ‎1‎ ‎11‎ ‎1‎ ‎1‎ ‎22‎ ‎9‎ 则抽取的数据中3.3学生捐款情况的中位数是 ，数据的样本容量是 。‎ ‎12.在下图方框中设计一个美丽的中心对称图形并使它成为正方体的一种侧面展开图 ‎(第14题)‎ ‎ （第12题）‎ ‎13.“汽车驾驶员的座位设在前面而不是后面”这与“站得高，看得远”从数学原理上来说是为了 ‎ ‎ 。‎ ‎14. 如图，一串有黑有白，其排列有一定规律的珠子，被盒子遮住了一部分，则这串珠子被盒子遮住的部分有_________粒. ‎ ‎15.‎2008年8月8日，奥运会在我国首都北京举行，为强化奥运理念，营造奥运氛围，决定2008.1.1——2008.9.30，中央电视台体育频道更名为奥运频道。若小名家的电视有36个频道，其中有13个中央台（含一个奥运频道），23个卫星台，小明随意选一台，恰巧是中央台的概率是 ，恰好是奥运频道的概率是 。‎ ‎16.如图，△ABC顶角是360的等腰三角形（底与腰的比为的三角形是黄金三角形），若△ABC、△BDC、△DEC都是黄金三角形，已知AB=4，则DE= 。‎ ‎ （第16题）‎ 得分 评卷人 ‎ ‎ 三、（每题8分，共16分）‎ ‎17.先化简，在求值： ，其中x=cos450‎ 座位号 ‎18. 我们给出如下定义：若一个四边形的两条对角线相等，则称这个四边形为等对角线四边形．请解答下列问题：‎ ‎（1）写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称；‎ ‎（2）探究：当等对角线四边形中两条对角线所夹锐角为时，这对角所对的两边之和与其中一条对角线的大小关系，并证明你的结论．‎ 得分 评卷人 ‎ ‎ 四、（每题10分，共20分）‎ ‎19.2008年5月，吴国雄访问大陆，加速了大陆与台湾关系的正常化，我国为此也采取了一些措施：对原产台湾地区的15种水果实施进口零关税措施，扩大了台湾水果在大陆的销售，促进了台湾地区经济的发展。某大陆经销商销售了台湾水果凤梨。根据以往销售经验，每天的售价与销售量之间有如下关系：‎ 每千克售价/元 ‎38‎ ‎37‎ ‎36‎ ‎35‎ ‎……‎ ‎20‎ 每天销售/kg ‎50‎ ‎52‎ ‎54‎ ‎56‎ ‎……‎ ‎86‎ 设当单价从38元/kg下调了x元，销售量为y。‎ （1） 写出y与x之间的函数关系式。并回答：如果凤梨进价为20元/kg，某天的销售价定为30元/kg，这天的销售利润是多少？‎ （2） 目前两岸还未直接通航，运输要绕行，需耗时一周（7天），凤梨最长保存时间为30天，若每天售价不低于30元/kg，问一次进货最多只能是多少千克？‎ ‎（‎ ‎20.如图，已知AB是⊙O直径，AC是⊙O弦，点D是ABC的中点，弦DE⊥AB，垂足为F，DE交AC于点G.‎ ‎（1）若过点E作⊙O的切线ME，交AC的延长线于点M（请补完整图形），试问：ME=MG是否成立？若成立，请证明；若不成立，请说明理由。‎ ‎（2）在满足第（2）问的条件下，已知AF=3，FB=，求AG与GM的比。‎ ‎ （第20题）‎ 得分 评卷人 ‎ ‎ 五、（每题10分，共20分）‎ ‎21. 丹东市十九中学对九年级学生进行“综合素质”评价，评价的结果为A(优)、B(良好)、C(合格)、D(不合格)四个等级．现从中抽测了若干名学生的“综合素质”等级作为样本进行数据处理，并作出如图所示的统计图，已知图中从左到右的四个长方形的高的比为：14∶9∶6∶‎ ‎1，评价结果为D等级的有2人，请你回答以下问题：‎ ‎(1)共抽测了多少人？‎ ‎(2)样本中B等级的频率是多少？C等级的频率是多少？‎ ‎(3)如果要绘制扇形统计图，A、D两个等级在扇形统计图中所占的圆心角分别是多少度？‎ ‎(4)十九中学2008届的毕业生共660人，“综合素质”等级为A的学生才能报考重点高中，请你计算该校大约有多少名学生可以报考重点高中？‎ ‎(第21题)‎ D C B A 等级 人数 ‎22.小华与小丽设计了两种游戏：‎ 游戏的规则：用3张数字分别是2，3，4的扑克牌，将牌洗匀后背面朝上放置在桌面上，第一次随机抽出一张牌记下数字后再原样放回，洗匀后再第二次随机抽出一张牌记下数字．若抽出的两张牌上的数字之和为偶数，则小华获胜；若两数字之和为奇数，则小丽获胜．‎ 游戏的规则：用4张数字分别是5，6，8，8的扑克牌，将牌洗匀后背面朝上放置在桌面上，小华先随机抽出一张牌，抽出的牌不放回，小丽从剩下的牌中再随机抽出一张牌．若小华抽出的牌面上的数字比小丽抽出的牌面上的数字大，则小华获胜；否则小丽获胜．‎ 请你帮小丽选择其中一种游戏，使她获胜的可能性较大，并说明理由．‎ 得分 评卷人 ‎ ‎ 六、（每题10分，共20分）‎ ‎23.丹东市“建设社会主义新农村”工作组到东港市大棚蔬菜生产基地指导菜农修建大棚种植蔬菜。通过调查得知：平均修建每公顷大棚要用支架、农膜等材料费2.7万元；购置滴灌装置，这项费用（万元）与大棚面积（公顷）的平方成正比，比例系数为0.9；另外每公顷种植蔬菜需要种子、化肥、农药等开支0.3万元。每公顷蔬菜平均可卖7.5万元。‎ ‎（1）基地的菜农共修建大棚x（公顷），当年收益（扣除修建和种植成本后）为y（万元）,写出y关于x的函数关系式。‎ ‎（2）若某菜农期望通过种植大棚蔬菜当年获利5万元收益，工作组应建议他修建多少公顷大棚？（用分数表示即可）‎ ‎（3）除种子、化肥、农药投资只能当年收益外，其他设施3年内不需增加投资仍可继续使用。如果按三年计算，是否大棚面积越大收益越大？修建面积为多少是可以获得最大利润？请帮工作组为基地修建大棚提一条合理化建议。‎ ‎24.如图a，∠EBF=90°，请按下列要求准确画图：‎ ① 在射线BE、BF上分别取点A、C，使BC＜AB＜2BC，连接AC得直角△ABC；‎ ② 在AB边上取一点M，使AM=BC，在射线CB边上取一点N，使CN=BM，直线AN、CM相交于点P．‎ ‎（1）请用量角器度量∠APM的度数为 （精确到1°）；‎ ‎（2）请用说理的方法求出∠APM的度数；‎ ‎（3）若将①中的条件“BC＜AB＜2BC”改为“AB＞2BC”，其他条件不变，你能自己在图b中画出图形，求出∠APM的度数吗？‎ ‎ （第24题）‎ 得分 评卷人 ‎ ‎ 七、（12分）‎ ‎25. 如图①，在直角坐标系中，点A的坐标为(1，0)，以OA为边在第一象限内作正方形OABC，点D是轴正半轴上一动点(OD＞1),连结BD，以BD为边在第一象限内作正方形DBFE，设M为正方形DBFE的中心，直线MA交y轴于点N．如果定义：只有一组对角是直角的四边形叫做损矩形．‎ ‎(1) 试找出图1中的一个损矩形．‎ ‎(2) 试说明(1)中找出的损矩形的四个顶点一定在同一个圆上．‎ ‎(3) 随着点D位置的变化，点N的位置是否会发生变化？若没有发生变化，求出点N的坐标；若发生变化，请说明理由．‎ ‎(4) 在图②中，过点M作MG⊥y轴于点G，连结DN，若四边形DMGN为损矩形，求D点坐标．‎ O B C F E M A D y N G A B D F E O C M N y ① ‎②‎ ‎ （第25题）‎ 得分 评卷人 ‎ ‎ 八、（14分）‎ ‎26. 如图，是一张放在平面直角坐标系中的矩形纸片，为原点，点在轴的正半轴上，点在轴的正半轴上，．‎ ‎（1）在边上取一点，将纸片沿翻折，使点落在边上的点处，求点，的坐标；‎ ‎（2）若过点的抛物线与轴相交于点，求抛物线的解析式和对称轴方程；‎ ‎（3）若（2）中的抛物线与轴交于点，在抛物线上是否存在点，使的内心在坐标轴上？若存在，求出点的坐标，若不存在，请说明理由．‎ ‎3‎ ‎5‎ ‎（4）若（2）中的抛物线与轴相交于点，点在线段上移动，作直线，当点移动到什么位置时，两点到直线的距离之和最大？请直接写出此时点的坐标及直线的解析式．‎ ‎ ‎ ‎(第26题)‎