- 2021-11-11 发布 |
- 37.5 KB |
- 10页

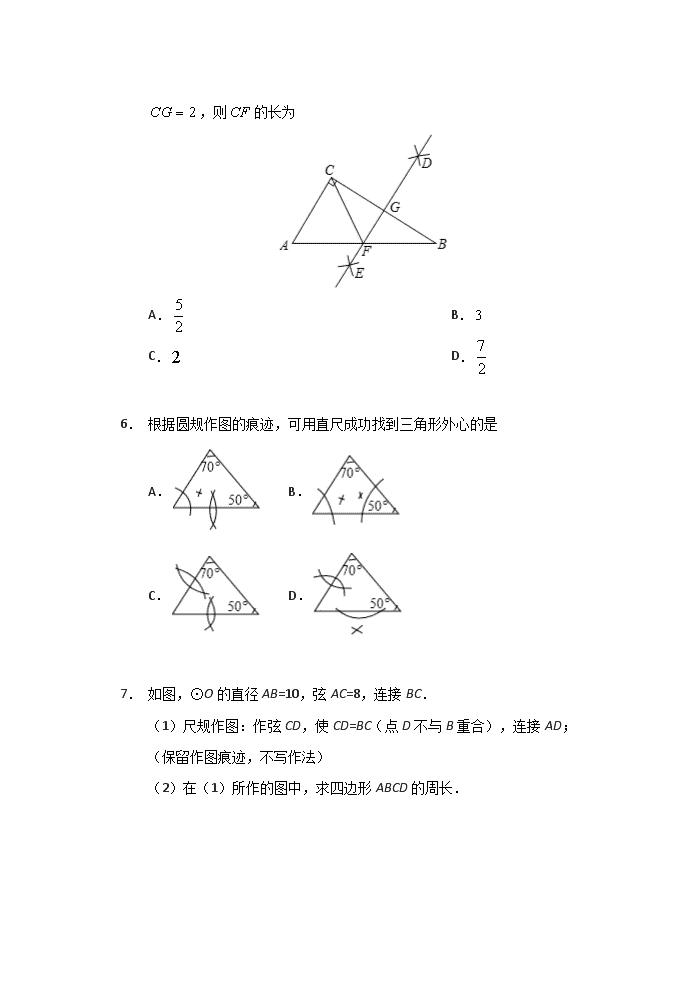
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
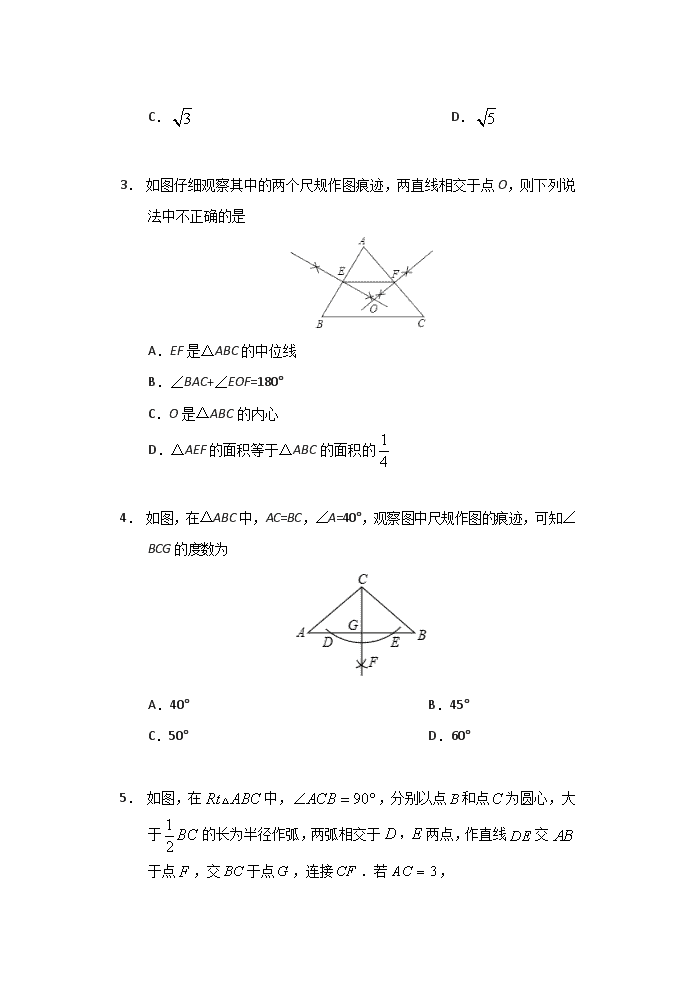
2020年绵阳市中考数学考点训练4:尺规作图(含答案)
尺规作图 1. 如图,在四边形ABCD中,AD∥BC,∠D=90°,AD=4,BC=3.分别以点A,C为圆心,大于AC长为半径作弧,两弧交于点E,作射线BE交AD于点F,交AC于点O.若点O是AC的中点,则CD的长为 A. B.4 C.3 D. 2. 如图,在△ABC中,AB=AC,以点C为圆心,CB长为半径画弧,交AB于点B和点D,再分别以点B,D为圆心,大于BD长为半径画弧,两弧相交于点M,作射线CM交AB于点E.若AE=2,BE=1,则EC的长度是 A.2 B.3 C. D. 3. 如图仔细观察其中的两个尺规作图痕迹,两直线相交于点O,则下列说法中不正确的是 A.EF是△ABC的中位线 B.∠BAC+∠EOF=180° C.O是△ABC的内心 D.△AEF的面积等于△ABC的面积的 4. 如图,在△ABC中,AC=BC,∠A=40°,观察图中尺规作图的痕迹,可知∠BCG的度数为 A.40° B.45° C.50° D.60° 5. 如图,在中,,分别以点和点为圆心,大于的长为半径作弧,两弧相交于两点,作直线交于点,交于点,连接.若, ,则的长为 A. B. C. D. 6. 根据圆规作图的痕迹,可用直尺成功找到三角形外心的是 A. B. C. D. 7. 如图,⊙O的直径AB=10,弦AC=8,连接BC. (1)尺规作图:作弦CD,使CD=BC(点D不与B重合),连接AD;(保留作图痕迹,不写作法) (2)在(1)所作的图中,求四边形ABCD的周长. 8. 如图,已知等腰顶角. (1)在AC上作一点D,使(要求:尺规作图,保留作图痕迹,不必写作法和证明,最后用黑色墨水笔加墨); (2)求证:是等腰三角形. 9. 如图,点D在△ABC的AB边上. (1)作∠BDC的平分线DE,交BC于点E(用尺规作图法,保留作图痕迹,不要求写作法); (2)在(1)的条件下,若直线DE与直线AC平行,则∠ACD=∠A吗?为什么? 10. 如图,在△ABC中,点D是AB边上的一点. (1)请用尺规作图法,在△ABC内,求作∠ADE,使∠ADE=∠B,DE交AC于E;(不要求写作法,保留作图痕迹) (2)在(1)的条件下,若=2,求的值. 11. 如图,点和点在内部. (1)请你作出点,使点到点和点的距离相等,且到两边的距离也相等(保留作图痕迹,不写作法); (2)请说明作图理由. 12. 如图,在中,,点是上一点. (1)尺规作图:作,使与、都相切.(不写作法与证明,保留作图痕迹) (2)若与相切于点D,与的另一个交点为点,连接 、,求证:. 13. 如图是由边长为1的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形ABCD的顶点在格点上,点E是边DC与网格线的交点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由. (1)如图1,过点A画线段AF,使AF∥DC,且AF=DC. (2)如图1,在边AB上画一点G,使∠AGD=∠BGC. (3)如图2,过点E画线段EM,使EM∥AB,且EM=AB. 答案 1. A 2. D 3. C 4. C 5. A 6. C 7. (1)如图,线段CD即为所求. (2)连接BD,OC交于点E,设OE=x. ∵AB是直径, ∴∠ACB=90°, ∴BC6, ∵BC=CD,∴, ∴OC⊥BD于E.∴BE=DE, ∵BE2=BC2-EC2=OB2-OE2, ∴62-(5-x)2=52-x2,解得x, ∵BE=DE,BO=OA, ∴AD=2OE, ∴四边形ABCD的周长=6+6+10. 8. (1)如图,点D为所作. (2)∵, ∴, ∵, ∴, ∴, ∴, ∴是等腰三角形. 9. (1)如图所示,DE即为所求. (2)∠ACD=∠A. ∵直线DE与直线AC平行, 理由:∴∠A=∠BDE,∠EDC=∠ACD, 又∵∠BDE=∠CDE, ∴∠ACD=∠A. 10. (1)如图,∠ADE为所作. (2)∵∠ADE=∠B, ∴DE∥BC, ∴=2. 11. (1)如图,作∠AOB的角平分线与线段MN的垂直平分线交于P点,即点到点和点的距离相等,且到两边的距离也相等. (2)理由:角的平分线上的点到角的两边的距离相等、直平分线上的点到线段两端点的距离相等. 12. (1)如图,及为所求. (2)连接. ∵是的切线, ∴, ∴,即, ∵是直径,∴, ∴, ∵,∴,∴, 又, ∴∽, ∴, ∴. 13. (1)如图所示,线段AF即为所求. (2)如图所示,点G即为所求. (3)如图所示,线段EM即为所求.查看更多