- 2021-11-11 发布 |
- 37.5 KB |
- 75页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版九上第4章图形的相似测试卷(共3套含解析)
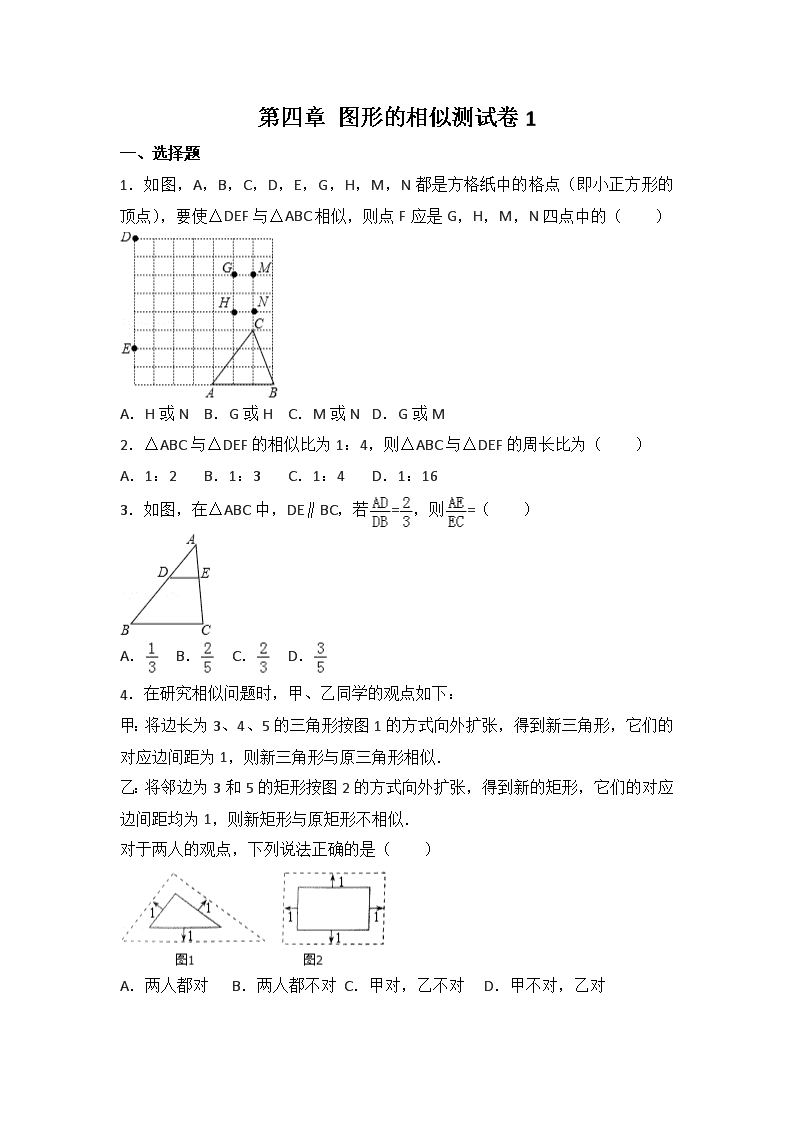
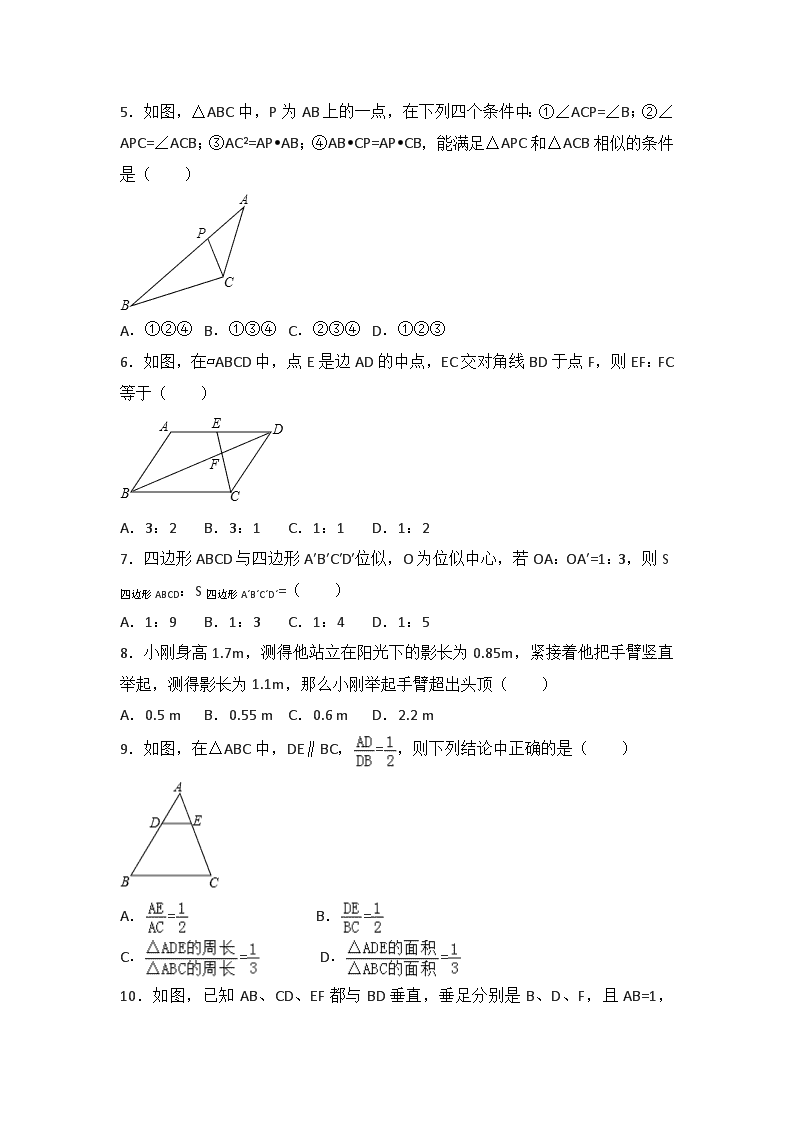
第四章 图形的相似测试卷 1 一、选择题 1.如图,A,B,C,D,E,G,H,M,N 都是方格纸中的格点(即小正方形的 顶点),要使△DEF 与△ABC 相似,则点 F 应是 G,H,M,N 四点中的( ) A.H 或 N B.G 或 H C.M 或 N D.G 或 M 2.△ABC 与△DEF 的相似比为 1:4,则△ABC 与△DEF 的周长比为( ) A.1:2 B.1:3 C.1:4 D.1:16 3.如图,在△ABC 中,DE∥BC,若 = ,则 =( ) A. B. C. D. 4.在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为 3、4、5 的三角形按图 1 的方式向外扩张,得到新三角形,它们的 对应边间距为 1,则新三角形与原三角形相似. 乙:将邻边为 3 和 5 的矩形按图 2 的方式向外扩张,得到新的矩形,它们的对应 边间距均为 1,则新矩形与原矩形不相似. 对于两人的观点,下列说法正确的是( ) A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对 5.如图,△ABC 中,P 为 AB 上的一点,在下列四个条件中:①∠ACP=∠B;②∠ APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC 和△ACB 相似的条件 是( ) A.①②④ B.①③④ C.②③④ D.①②③ 6.如图,在▱ABCD 中,点 E 是边 AD 的中点,EC 交对角线 BD 于点 F,则 EF:FC 等于( ) A.3:2 B.3:1 C.1:1 D.1:2 7.四边形 ABCD 与四边形 A′B′C′D′位似,O 为位似中心,若 OA:OA′=1:3,则 S 四边形 ABCD:S 四边形 A´B´C´D´=( ) A.1:9 B.1:3 C.1:4 D.1:5 8.小刚身高 1.7m,测得他站立在阳光下的影长为 0.85m,紧接着他把手臂竖直 举起,测得影长为 1.1m,那么小刚举起手臂超出头顶( ) A.0.5 m B.0.55 m C.0.6 m D.2.2 m 9.如图,在△ABC 中,DE∥BC, = ,则下列结论中正确的是( ) A. = B. = C. = D. = 10.如图,已知 AB、CD、EF 都与 BD 垂直,垂足分别是 B、D、F,且 AB=1, CD=3,那么 EF 的长是( ) A. B. C. D. 二、填空题 11.若 ,则 = . 12.如果 = = =k(b+d+f≠0),且 a+c+e=3(b+d+f),那么 k= . 13.已知一个三角形的三边长分别为 6,8 和 10,与其相似的一个三角形的最短 边长为 18,则较小三角形与较大三角形的相似比 k= . 14.在△ABC 中,AB=12cm,BC=18cm,AC=24cm,另一个与它相似的△A′B′C′的 周长为 18cm,则△A′B′C 各边长分别为 . 15.如图,一束光线从点 A(3,3)出发,经过 y 轴上点 C 反射后经过点 B(1, 0),则光线从点 A 到点 B 经过的路径长为 . 16.如图,AB、CD 相交于点 O,OC=2,OD=3,AC∥BD,EF 是△ODB 的中位线, 且 EF=2,则 AC 的长为 . 17.如图,在△ABC 中,DE∥BC, = ,△ADE 的面积是 8,则△ABC 的面积 为 . 18.如图,在正方形 ABCD 中,点 E 是 BC 边上一点,且 BE:EC=2:1,AE 与 BD 交于点 F,则△AFD 与四边形 DEFC 的面积之比是 . 三、解答题 19.已知线段 a,b,c,d 成比例,且 a=6dm,b=3dm,d= dm,求线段 c 的长 度. 20.(6 分)若 = ,求 的值. 21.已知 a、b、c 是△ABC 的三边,且满足 ,且 a+b+c=12,请你 探索△ABC 的形状. 22.如图,△ABC 中,CD 是边 AB 上的高,且 = . (1)求证:△ACD∽△CBD; (2)求∠ACB 的大小. 23.如图,在正方形 ABCD 中,E、F 分别是边 AD、CD 上的点,AE=ED,DF= DC,连接 EF 并延长交 BC 的延长线于点 G. (1)求证:△ABE∽△DEF; (2)若正方形的边长为 4,求 BG 的长. 24.某小区居民筹集资金 1600 元,计划在两底分别为 10m、20m 梯形空地上种 植种植花木,如图: (1)他们在△AMD 和△BMC 地带上种植太阳花,单价为 8 元/m2,当△AMD 地 带种满花后(图中阴影部分),共花了 160 元,计算种满△BMC 地带所需费 用. (2)若其余地带有玫瑰、茉莉两种可供选择,单价分别为 12 元/m2、10 元/m2, 应选哪种花木,刚好用完所筹资金? 25.如图,已知在△ABC 和△EBD 中, . (1)若△ABC 与△EBD 的周长之差为 60cm,求这两个三角形的周长. (2)若△ABC 与△EBD 的面积之和为 812cm2,求这两个三角形的面积. 26.某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度, 两人在确保无安全隐患的情况下,先在河岸边选择了一点 B(点 B 与河对岸岸边 上的一棵树的底部点 D 所确定的直线垂直于河岸). ①小明在 B 点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部 点 D 处,如图所示,这时小亮测得小明眼睛距地面的距离 AB=1.7 米; ②小明站在原地转动 180°后蹲下,并保持原来的观察姿态(除身体重心下移外, 其他姿态均不变),这时视线通过帽檐落在了 DB 延长线上的点 E 处,此时小亮 测得 BE=9.6 米,小明的眼睛距地面的距离 CB=1.2 米. 根据以上测量过程及测量数据,请你求出河宽 BD 是多少米? 答案解析 一、选择题 1.如图,A,B,C,D,E,G,H,M,N 都是方格纸中的格点(即小正方形的 顶点),要使△DEF 与△ABC 相似,则点 F 应是 G,H,M,N 四点中的( ) A.H 或 N B.G 或 H C.M 或 N D.G 或 M 【考点】相似三角形的判定. 【专题】压轴题;网格型;数形结合. 【分析】根据两三角形三条边对应成比例,两三角形相似进行解答. 【解答】解:设小正方形的边长为 1,则△ABC 的各边分别为 3、 、 ,只 能 F 是 M 或 N 时,其各边是 6、2 ,2 .与△ABC 各边对应成比例,故选 C. 【点评】此题考查三边对应成比例,两三角形相似判定定理的应用. 2.△ABC 与△DEF 的相似比为 1:4,则△ABC 与△DEF 的周长比为( ) A.1:2 B.1:3 C.1:4 D.1:16 【考点】相似三角形的性质. 【分析】由相似三角形周长的比等于相似比即可得出结果. 【解答】解:∵△ABC 与△DEF 的相似比为 1:4, ∴△ABC 与△DEF 的周长比为 1:4; 故选:C. 【点评】本题考查了相似三角形的性质;熟记相似三角形周长的比等于相似比是 解决问题的关键. 3.如图,在△ABC 中,DE∥BC,若 = ,则 =( ) A. B. C. D. 【考点】平行线分线段成比例. 【分析】直接利用平行线分线段成比例定理写出答案即可. 【解答】解:∵DE∥BC, ∴ = = , 故选 C. 【点评】本题考查了平行线分线段成比例定理,了解定理的内容是解答本题的关 键,属于基础定义或定理,难度不大. 4.在研究相似问题时,甲、乙同学的观点如下: 甲:将边长为 3、4、5 的三角形按图 1 的方式向外扩张,得到新三角形,它们的 对应边间距为 1,则新三角形与原三角形相似. 乙:将邻边为 3 和 5 的矩形按图 2 的方式向外扩张,得到新的矩形,它们的对应 边间距均为 1,则新矩形与原矩形不相似. 对于两人的观点,下列说法正确的是( ) A.两人都对 B.两人都不对 C.甲对,乙不对 D.甲不对,乙对 【考点】相似三角形的判定;相似多边形的性质. 【专题】数形结合. 【分析】甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′,即可证得∠A=∠A′,∠ B=∠B′,可得△ABC∽△A′B′C′; 乙:根据题意得:AB=CD=3,AD=BC=5,则 A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7, 则可得 ,即新矩形与原矩形不相似. 【解答】解:甲:根据题意得:AB∥A′B′,AC∥A′C′,BC∥B′C′, ∴∠A=∠A′,∠B=∠B′, ∴△ABC∽△A′B′C′, ∴甲说法正确; 乙:∵根据题意得:AB=CD=3,AD=BC=5,则 A′B′=C′D′=3+2=5,A′D′=B′C′=5+2=7, ∴ , , ∴ , ∴新矩形与原矩形不相似. ∴乙说法正确. 故选:A. 【点评】此题考查了相似三角形以及相似多边形的判定.此题难度不大,注意掌 握数形结合思想的应用. 5.如图,△ABC 中,P 为 AB 上的一点,在下列四个条件中:①∠ACP=∠B;②∠ APC=∠ACB;③AC2=AP•AB;④AB•CP=AP•CB,能满足△APC 和△ACB 相似的条件 是( ) A.①②④ B.①③④ C.②③④ D.①②③ 【考点】相似三角形的判定. 【分析】根据有两组角对应相等的两个三角形相似可对①②进行判断;根据两组 对应边的比相等且夹角对应相等的两个三角形相似可对③④进行判断. 【解答】解:当∠ACP=∠B, ∠A 公共, 所以△APC∽△ACB; 当∠APC=∠ACB, ∠A 公共, 所以△APC∽△ACB; 当 AC2=AP•AB, 即 AC:AB=AP:AC, ∠A 公共, 所以△APC∽△ACB; 当 AB•CP=AP•CB,即 = , 而∠PAC=∠CAB, 所以不能判断△APC 和△ACB 相似. 故选 D. 【点评】本题考查了相似三角形的判定:两组对应边的比相等且夹角对应相等的 两个三角形相似;有两组角对应相等的两个三角形相似. 6.如图,在▱ABCD 中,点 E 是边 AD 的中点,EC 交对角线 BD 于点 F,则 EF:FC 等于( ) A.3:2 B.3:1 C.1:1 D.1:2 【考点】相似三角形的判定与性质. 【专题】几何图形问题. 【分析】根据题意得出△DEF∽△BCF,进而得出 = ,利用点 E 是边 AD 的中 点得出答案即可. 【解答】解:∵▱ABCD,故 AD∥BC, ∴△DEF∽△BCF, ∴ = , ∵点 E 是边 AD 的中点, ∴AE=DE= AD, ∴ = . 故选:D. 【点评】此题主要考查了平行四边形的性质以及相似三角形的判定与性质等知识, 得出△DEF∽△BCF 是解题关键. 7.四边形 ABCD 与四边形 A′B′C′D′位似,O 为位似中心,若 OA:OA′=1:3,则 S 四边形 ABCD:S 四边形 A´B´C´D´=( ) A.1:9 B.1:3 C.1:4 D.1:5 【考点】位似图形的性质. 【分析】四边形 ABCD 与四边形 A′B′C′D′位似,四边形 ABCD∽四边形 A′B′C′D′,可 知 AD∥A′D′,△OAD∽△OA′D′,求出相似比从而求得 S 四边形 ABCD:S四边形 A´B´C´D´的 值. 【解答】解:∵四边形 ABCD 与四边形 A′B′C′D′位似, ∴四边形 ABCD∽四边形 A′B′C′D′, ∴AD∥A′D′, ∴△OAD∽△OA′D′, ∴OA:O′A′=AD:A′D′=1:3, ∴S 四边形 ABCD:S 四边形 A´B´C´D´=1:9. 故选:A. 【点评】本题考查了位似的相关知识,位似是相似的特殊形式,位似比等于相似 比,其对应的面积比等于相似比的平方. 8.小刚身高 1.7m,测得他站立在阳光下的影长为 0.85m,紧接着他把手臂竖直 举起,测得影长为 1.1m,那么小刚举起手臂超出头顶( ) A.0.5 m B.0.55 m C.0.6 m D.2.2 m 【考点】利用影子测量物体的高度. 【分析】根据在同一时物体的高度和影长成正比,设出手臂竖直举起时总高度 x,即可列方程解出 x 的值,再减去身高即可得出小刚举起的手臂超出头顶的高 度. 【解答】解:设手臂竖直举起时总高度 xm,列方程得: = , 解得 x=2.2, 2.2﹣1.7=0.5m, 所以小刚举起的手臂超出头顶的高度为 0.5m. 故选:A. 【点评】本题考查了相似三角形的应用,解答此题的关键是明确在同一时刻物体 的高度和影长成正比. 9.如图,在△ABC 中,DE∥BC, = ,则下列结论中正确的是( ) A. = B. = C. = D. = 【考点】相似三角形的判定与性质. 【分析】由 DE∥BC,可得△ADE∽△ABC,然后由相似三角形的对应边成比例可 得 ,然后由 = ,即可判断 A、B 的正误,然后根据相似三角形的 周长之比等于相似比,面积之比等于相似比的平方即可判断 C、D 的正误. 【解答】解:∵DE∥BC, ∴△ADE∽△ABC, ∴ , ∵ = , ∵ = , 故 A、B 选项均错误; ∵△ADE∽△ABC, ∴ = = , =( )2= , 故 C 选项正确,D 选项错误. 故选 C. 【点评】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形 的对应边之比等于相似比;相似三角形的周长之比等于相似比;相似三角形的面 积之比等于相似比的平方. 10.如图,已知 AB、CD、EF 都与 BD 垂直,垂足分别是 B、D、F,且 AB=1, CD=3,那么 EF 的长是( ) A. B. C. D. 【考点】相似三角形的判定与性质. 【分析】易证△DEF∽△DAB,△BEF∽△BCD,根据相似三角形的性质可得 = , = ,从而可得 + = + =1.然后把 AB=1,CD=3 代入即可求出 EF 的值. 【解答】解:∵AB、CD、EF 都与 BD 垂直, ∴AB∥CD∥EF, ∴△DEF∽△DAB,△BEF∽△BCD, ∴ = , = , ∴ + = + = =1. ∵AB=1,CD=3, ∴ + =1, ∴EF= . 故选 C. 【点评】本题主要考查的是相似三角形的判定与性质,发现 + =1 是解决本 题的关键. 二、填空题 11.若 ,则 = . 【考点】比例的性质. 【专题】常规题型. 【分析】根据比例的性质求出 的值,然后两边加 1 进行计算即可得解. 【解答】解:∵ , ∴ ﹣2= , =2+ = , ∴ +1= +1, 即 = . 故答案为: . 【点评】本题考查了比例的性质,根据已知条件求出 的值是解题的关键. 12.如果 = = =k(b+d+f≠0),且 a+c+e=3(b+d+f),那么 k= 3 . 【考点】比例的性质. 【分析】根据等比性质,可得答案. 【解答】解:由等比性质,得 k= = =3, 故答案为:3. 【 点 评 】 本 题 考 查 了 比 例 的 性 质 , 利 用 了 等 比 性 质 : = = =k⇒k= = . 13.已知一个三角形的三边长分别为 6,8 和 10,与其相似的一个三角形的最短 边长为 18,则较小三角形与较大三角形的相似比 k= . 【考点】相似三角形的性质. 【分析】由一个三角形的三边长分别为 6,8 和 10,与其相似的一个三角形的最 短边长为 18,根据相似比等于对应边的比,即可求得答案. 【解答】解:∵一个三角形的三边长分别为 6,8 和 10,与其相似的一个三角形 的最短边长为 18, ∴较小三角形与较大三角形的相似比 k= = . 故答案为: . 【点评】此题考查了相似比的定义.此题比较简单,解题的关键是熟记定义. 14.在△ABC 中,AB=12cm,BC=18cm,AC=24cm,另一个与它相似的△A′B′C′的 周长为 18cm,则△A′B′C 各边长分别为 4cm,6cm,8cm . 【考点】相似三角形的性质. 【分析】由△A′B′C′∽△ABC,根据相似三角形周长的比等于相似比,即可求得答 案. 【解答】解:∵△A′B′C′∽△ABC, ∴△A′B′C′的周长:△ABC 的周长=A′B′:AB, ∵在△ABC 中,AB=12cm,BC=18cm,AC=24cm, ∴△ABC 的周长为:54cm, ∵△A′B′C′的周长为 18cm, ∴A′B′:AB=A′C′:AC=B′C′:BC= , ∴A′B′=4cm,B′C′=6cm,A′C′=8cm. 故答案为:4cm,6cm,8cm. 【点评】此题考查了相似三角形的性质,熟练掌握相似三角形的性质是解题的关 键. 15.如图,一束光线从点 A(3,3)出发,经过 y 轴上点 C 反射后经过点 B(1, 0),则光线从点 A 到点 B 经过的路径长为 5 . 【考点】利用镜子的反射原理. 【专题】计算题;压轴题. 【分析】延长 AC 交 x 轴于 B′.根据光的反射原理,点 B、B′关于 y 轴对称, CB=CB′.路径长就是 AB′的长度.结合 A 点坐标,运用勾股定理求解. 【解答】解:如图所示, 延长 AC 交 x 轴于 B′.则点 B、B′关于 y 轴对称,CB=CB′. 作 AD⊥x 轴于 D 点.则 AD=3,DB′=3+1=4. ∴AB′=AC+CB′=AC+CB=5. 即光线从点 A 到点 B 经过的路径长为 5. 【点评】本题考查了直角三角形的有关知识,同时渗透光学中反射原理,构造直 角三角形是解决本题关键. 16.如图,AB、CD 相交于点 O,OC=2,OD=3,AC∥BD,EF 是△ODB 的中位线, 且 EF=2,则 AC 的长为 . 【考点】相似三角形的性质. 【分析】根据三角形的中位线平行于第三边并且等于第三边的一半求出 DB,再 根据相似三角形对应边成比例列式计算即可得解. 【解答】解:∵EF 是△ODB 的中位线, ∴DB=2EF=2×2=4, ∵AC∥BD, ∴△AOC∽△BOD, ∴ = , 即 = , 解得 AC= . 故答案为: . 【点评】本题考查了三角形的中位线平行于第三边并且等于第三边的一半,相似 三角形的判定与性质,熟记定理与性质是解题的关键. 17.如图,在△ABC 中,DE∥BC, = ,△ADE 的面积是 8,则△ABC 的面积 为 18 . 【考点】相似三角形的判定与性质. 【分析】根据相似三角形的判定,可得△ADE∽△ABC,根据相似三角形的性质, 可得答案. 【解答】解;∵在△ABC 中,DE∥BC, ∴△ADE∽△ABC. ∵ = , ∴ =( )2= , , ∴S△ABC=18, 故答案为:18. 【点评】本题考查了相似三角形判定与性质,利用了相似三角形的判定与性 质. 18.如图,在正方形 ABCD 中,点 E 是 BC 边上一点,且 BE:EC=2:1,AE 与 BD 交于点 F,则△AFD 与四边形 DEFC 的面积之比是 9:11 . 【考点】相似三角形的判定与性质. 【专题】压轴题. 【分析】根据题意,先设 CE=x,S△BEF=a,再求出 S△ADF 的表达式,利用四部分的 面积和等于正方形的面积,得到 x 与 a 的关系,那么两部分的面积比就可以求出 来. 【解答】解:设 CE=x,S△BEF=a, ∵CE=x,BE:CE=2:1, ∴BE=2x,AD=BC=CD=AD=3x; ∵BC∥AD∴∠EBF=∠ADF, 又∵∠BFE=∠DFA; ∴△EBF∽△ADF ∴S△BEF:S△ADF= = = ,那么 S△ADF= a. ∵S△BCD﹣S△BEF=S 四边形 EFDC=S 正方形 ABCD﹣S△ABE﹣S△ADF, ∴ x2﹣a=9x2﹣ ×3x•2x﹣ , 化简可求出 x2= ; ∴S△AFD:S 四边形 DEFC= : = : =9:11,故答案为 9:11. 【点评】此题运用了相似三角形的判定和性质,还用到了相似三角形的面积比等 于相似比的平方. 三、解答题 19.已知线段 a,b,c,d 成比例,且 a=6dm,b=3dm,d= dm,求线段 c 的长 度. 【考点】成比例线段. 【分析】根据比例线段的定义得出 = ,即 = ,解之可得 c. 【解答】解:根据题意, = ,即 = , 解得:c=3, 答:线段 c 的长度为 3dm. 【点评】本题主要考查比例线段,掌握比例线段的定义是关键. 20.若 = ,求 的值. 【考点】比例的性质. 【分析】首先由已知条件可得 x= ,然后再代入 即可求值. 【解答】解:∵ = , ∴8x﹣6y=x﹣y, x= , ∴ = = . 【点评】此题主要考查了比例的性质,关键是掌握内项之积等于外项之积. 21.已知 a、b、c 是△ABC 的三边,且满足 ,且 a+b+c=12,请你 探索△ABC 的形状. 【考点】比例的性质. 【专题】探究型. 【分析】令 =k.根据 a+b+c=12,得到关于 k 的方程,求得 k 值, 再进一步求得 a,b,c 的值,从而判定三角形的形状. 【解答】解:令 =k. ∴a+4=3k,b+3=2k,c+8=4k, ∴a=3k﹣4,b=2k﹣3,c=4k﹣8. 又∵a+b+c=12, ∴(3k﹣4)+(2k﹣3)+(4k﹣8)=12, ∴k=3. ∴a=5,b=3,c=4. ∴△ABC 是直角三角形. 【点评】此题能够利用方程求得 k 的值,进一步求得三角形的三边长,根据勾股 定理的逆定理判定三角形的形状. 22.如图,△ABC 中,CD 是边 AB 上的高,且 = . (1)求证:△ACD∽△CBD; (2)求∠ACB 的大小. 【考点】相似三角形的判定与性质. 【分析】(1)由两边对应成比例且夹角相等的两个三角形相似,即可证明△ACD ∽△CBD; (2)由(1)知△ACD∽△CBD,然后根据相似三角形的对应角相等可得:∠A=∠ BCD,然后由∠A+∠ACD=90°,可得:∠BCD+∠ACD=90°,即∠ACB=90°. 【解答】(1)证明:∵CD 是边 AB 上的高, ∴∠ADC=∠CDB=90°, ∵ = . ∴△ACD∽△CBD; (2)解:∵△ACD∽△CBD, ∴∠A=∠BCD, 在△ACD 中,∠ADC=90°, ∴∠A+∠ACD=90°, ∴∠BCD+∠ACD=90°, 即∠ACB=90°. 【点评】此题考查了相似三角形的判定与性质,解题的关键是:熟记相似三角形 的判定定理与性质定理. 23.如图,在正方形 ABCD 中,E、F 分别是边 AD、CD 上的点,AE=ED,DF= DC,连接 EF 并延长交 BC 的延长线于点 G. (1)求证:△ABE∽△DEF; (2)若正方形的边长为 4,求 BG 的长. 【考点】相似三角形的判定;平行线分线段成比例. 【专题】计算题;证明题. 【分析】(1)利用正方形的性质,可得∠A=∠D,根据已知可得 ,根据有 两边对应成比例且夹角相等三角形相似,可得△ABE∽△DEF; (2)根据平行线分线段成比例定理,可得 CG 的长,即可求得 BG 的长. 【解答】(1)证明:∵ABCD 为正方形, ∴AD=AB=DC=BC,∠A=∠D=90°, ∵AE=ED, ∴ , ∵DF= DC, ∴ , ∴ , ∴△ABE∽△DEF; (2)解:∵ABCD 为正方形, ∴ED∥BG, ∴ , 又∵DF= DC,正方形的边长为 4, ∴ED=2,CG=6, ∴BG=BC+CG=10. 【点评】此题考查了相似三角形的判定(有两边对应成比例且夹角相等三角形相 似)、正方形的性质、平行线分线段成比例定理等知识的综合应用.解题的关键 是数形结合思想的应用. 24.某小区居民筹集资金 1600 元,计划在两底分别为 10m、20m 梯形空地上种 植种植花木,如图: (1)他们在△AMD 和△BMC 地带上种植太阳花,单价为 8 元/m2,当△AMD 地 带种满花后(图中阴影部分),共花了 160 元,计算种满△BMC 地带所需费 用. (2)若其余地带有玫瑰、茉莉两种可供选择,单价分别为 12 元/m2、10 元/m2, 应选哪种花木,刚好用完所筹资金? 【考点】相似三角形的性质. 【专题】应用题. 【分析】(1)易得△AMD∽△BMC,根据 BC=2AD 可得 S△BMC=4S△AMD,据此可得 种满△BMC 的花费; (2)根据每平方米 8 元来看,△AMD 面积为 20 平米方米,△BMC 面积为 80 平 方米,因此可以得出梯形的高也就是两三角形高的和为 12 米,那么可得梯形面 积为 180 平方米,还有 80 平方米未种,800 元未用,所以要选择每平方米十元 的茉莉花. 【解答】解:(1)∵四边形 ABCD 是梯形, ∴AD∥BC, ∴∠MAD=∠MCB,∠MDA=∠MBC, ∴△AMD∽△CMB, ∴S△AMD:S△BMC=(10:20 )2=1:4. ∵种植△AMD 地带花费 160 元,单价为 8 元/m2, ∴S△AMD=20m2, ∴S△CMB=80m2, ∴△BMC 地带所需的费用为 8×80=640(元); (2)设△AMD 的高为 h1,△BMC 的高为 h2,梯形 ABCD 的高为 h. ∵S△AMD= ×10h1=20, ∴h1=4, ∵S△BCM= ×20h2=80, ∴h2=8, ∴S 梯形 ABCD= (AD+BC)•h = ×(10+20)×(4+8) =180. ∴S△AMB+S△DMC=180﹣20﹣80=80(m2), ∵160+640+80×12=1760(元), 160+640+80×10=1600(元), ∴应种植茉莉花刚好用完所筹集的资金. 【点评】此题主要考查了相似三角形的性质以及应用;求得梯形的高是解决本题 的难点;用到的知识点为:相似三角形的面积比等于相似比的平方. 25.如图,已知在△ABC 和△EBD 中, . (1)若△ABC 与△EBD 的周长之差为 60cm,求这两个三角形的周长. (2)若△ABC 与△EBD 的面积之和为 812cm2,求这两个三角形的面积. 【考点】相似三角形的判定与性质. 【分析】(1)根据已知条件得到△ABC∽△DBE,根据相似三角形的性质:相似 三角形周长的比等于相似比即可得到结论; (2)根据已知条件得到△ABC∽△DBE,根据相似三角形的性质:相似三角形面 积的比等于相似比的平方即可得到结论; 【解答】解:(1)∵ , ∴△ABC∽△DBE, ∴△ABC 的周长:△EBD 的周长= , 设△ABC 的周长为 5k,△EBD 的周长为 2k, ∴5k﹣2k=60, ∴k=20, ∴△ABC 的周长=100cm,△EBD 的周长=40cm; (2)∵ , ∴△ABC∽△DBE, ∴ =( )2= , ∵△ABC 与△EBD 的面积之和为 812cm2, ∴S△ABC=812× =700. 【点评】本题考查了相似三角形的判定和性质,三角形的面积和周长,熟练掌握 相似三角形的判定和性质是解题的关键. 26.某一天,小明和小亮来到一河边,想用遮阳帽和皮尺测量这条河的大致宽度, 两人在确保无安全隐患的情况下,先在河岸边选择了一点 B(点 B 与河对岸岸边 上的一棵树的底部点 D 所确定的直线垂直于河岸). ①小明在 B 点面向树的方向站好,调整帽檐,使视线通过帽檐正好落在树的底部 点 D 处,如图所示,这时小亮测得小明眼睛距地面的距离 AB=1.7 米; ②小明站在原地转动 180°后蹲下,并保持原来的观察姿态(除身体重心下移外, 其他姿态均不变),这时视线通过帽檐落在了 DB 延长线上的点 E 处,此时小亮 测得 BE=9.6 米,小明的眼睛距地面的距离 CB=1.2 米. 根据以上测量过程及测量数据,请你求出河宽 BD 是多少米? 【考点】相似三角形的性质与判定. 【专题】几何图形问题. 【分析】根据题意求出∠BAD=∠BCE,然后根据两组角对应相等,两三角形相似 求出△BAD 和△BCE 相似,再根据相似三角形对应边成比例列式求解即可. 【解答】解:由题意得,∠BAD=∠BCE, ∵∠ABD=∠CBE=90°, ∴△BAD∽△BCE, ∴ = , ∴ = , 解得 BD=13.6. 答:河宽 BD 是 13.6 米. 【点评】本题考查了相似三角形的应用,读懂题目信息得到两三角形相等的角并 确定出相似三角形是解题的关键,也是本题的难点. 第四章 图形的相似测试卷 2 一、选择题 1.已知 xy=mn,则把它改写成比例式后,错误的是( ) A. = B. = C. = D. = 2.已知 ,那么 的值是( ) A.3 B.4 C.5 D.6 3.下列两个图形一定相似的是( ) A.两个矩形 B.两个等腰三角形 C.两个五边形 D.两个正方形 4.如果两个相似多边形面积的比是 4:9,那么这两个相似多边形对应边的比是 ( ) A.4:9 B.2:3 C.16:81 D.9:4 5.如图,四边形 ABCD 是平行四边形,E 是 BC 的延长线上一点,AE 与 CD 相交 于 F,与△CEF 相似的三角形有( )个. A.1 B.2 C.3 D.4 6.如图,D 为△ABC 边 BC 上一点,要使△ABD∽△CBA,应该具备下列条件中 的( ) A. = B. = C. = D. = 7.如图,在△ABC 中,若 DE∥BC, ,DE=3cm,则 BC 的长为( ) A.3cm B.6cm C.9cm D.12cm 8.如图,△ABC 中,∠A=78°,AB=4,AC=6.将△ABC 沿图示中的虚线剪开,剪 下的阴影三角形与原三角形不相似的是( ) A. B. C. D. 9.如图,线段 CD 两个端点的坐标分别为 C(3,3),D(4,1),以原点 O 为位 似中心,在第一象限内将线段 CD 放大为原来的 2 倍后得到线段 AB,则端点 B 的 坐标为( ) A.(6,6) B.(6,8) C.(8,6) D.(8,2) 10.关于对位似图形的表述,下列命题正确的有( ) ①相似图形一定是位似图形,位似图形一定是相似图形; ②位似图形一定有位似中心; ③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点, 那么这两个图形是位似图形; ④位似图形上任意一组对应点 P,P′与位似中心 O 的距离满足 OP=k•OP′. A.①②③④ B.②③④ C.②③ D.②④ 11.如图,在直角梯形 ABCD 中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC 的平分线分别交 AD、AC 于点 E,F,则 的值是( ) A. B. C. D. 二、填空题 12.如图,△OAC 和△BAD 都是等腰直角三角形,反比例函数在第四象限经过点 B,若 OA2﹣AB2=8,则 k 的值为 . 13.已知线段 AB=1,C 是线段 AB 的黄金分割点,且 AC<CB,则 AC 的长度 为 . 14.)如图,在△ABC 中,D、E 分别是 AB、BC 上的点,且 DE∥AC,若 S△BDE:S △CDE=1:4,则 S△BDE:S△ACD= . 15.一块矩形绸布的宽 AB=a m,长 AD=1m,按照图中所示的方式将它裁成相同 的 n 面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同, 即,那么 a 的值应当是 . 16.如图,小亮在晚上由路灯 A 走向路灯 B,当他走到点 C 时,发现身后他影子 的顶部刚好接触到路灯 A 的底部,当他向前再步行 12m 到达点 D 时,发现身前 他影子的顶部刚好接触到路灯 B 的底部.已知小亮的身高是 1.5m,两个路灯的 高度都是 9m.当小亮走到路灯 B 时,他在路灯 A 下的影长是 m. 三、解答题 17.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB,垂足为 D. (1)证明:△ACD∽△CBD; (2)已知 AD=2,BD=4,求 CD 的长. 18.如图,AD 是△ABC 的高,点 E,F 在边 BC 上,点 H 在边 AB 上,点 G 在边 AC 上,AD=80cm,BC=120cm. (1)若四边形 EFGH 是正方形,求正方形的面积. (2)若四边形 EFGH 是长方形,长方形的面积为 y,设 EF=x,则 y= .(含 x 的代数式),当 x= 时,y 最大,最大面积是 . 19.如图,在直角梯形 ABCD 中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8, 点 P 是 AB 上一个动点. (1)当 AP=3 时,△DAP 与△CBP 相似吗?请说明理由. (2)求 PD+PC 的最小值. 20.如图,在 Rt△ABC 中,∠ABC=90°,点 D 为 BC 边上的点,BE⊥AD 于点 E, 延长 BE 交 AC 于点 F. (1)证明:BE2=AE•DE; (2)若 =1, = ;并说明理由. 答案解析 一、选择题 1.已知 xy=mn,则把它改写成比例式后,错误的是( ) A. = B. = C. = D. = 【考点】比例的性质. 【分析】熟练掌握比例的性质是解题的关键. 【解答】解:A、两边同时乘以最简公分母 ny 得 xy=mn,与原式相等; B、两边同时乘以最简公分母 mx 得 xy=mn,与原式相等; C、两边同时乘以最简公分母 mn 得 xn=my,与原式不相等; D、两边同时乘以最简公分母 my 得 xy=mn,与原式相等; 故选 C. 【点评】解答此题应把每一个选项乘以最简公分母后与原式相比较看是否相 同. 2.已知 ,那么 的值是( ) A.3 B.4 C.5 D.6 【考点】比例的性质. 【分析】根据和比性质: = ⇒ = ,可得答案. 【解答】解:由 =2,得 = =3. 故选:A. 【点评】本题考查了比例的性质,利用和比性质是解题关键. 3.下列两个图形一定相似的是( ) A.两个矩形 B.两个等腰三角形 C.两个五边形 D.两个正方形 【考点】相似多边形的定义. 【分析】根据相似图形的定义,结合选项,用排除法求解. 【解答】解:A、两个矩形,对应角相等,对应边不一定成比例,故不符合题意; B、两个等腰三角形顶角不一定相等,故不符合题意; C、两个五边形,对应角相等,对应边不一定成比例,故不符合题意; D、两个正方形,形状相同,大小不一定相同,符合相似性定义,故符合题 意. 故选 D. 【点评】本题考查相似形的定义,熟悉各种图形的性质是解题的关键. 4.如果两个相似多边形面积的比是 4:9,那么这两个相似多边形对应边的比是 ( ) A.4:9 B.2:3 C.16:81 D.9:4 【考点】相似多边形的性质. 【分析】由两个相似多边形面积的比是 4:9,根据相似多边形的面积比等于相 似比的平方,即可求得答案. 【解答】解:∵两个相似多边形面积的比是 4:9, ∴这两个相似多边形对应边的比是 2:3. 故选 B. 【点评】此题考查了相似多边形的性质.注意熟记定理是解此题的关键. 5.如图,四边形 ABCD 是平行四边形,E 是 BC 的延长线上一点,AE 与 CD 相交 于 F,与△CEF 相似的三角形有( )个. A.1 B.2 C.3 D.4 【考点】相似三角形的判定. 【分析】根据已知及相似三角形的判定方法进行分析,从而得到图中与△CEF 相 似的三角形. 【解答】解:∵四边形 ABCD 是平行四边形, ∴AB∥CD,AD∥BC, ∴∠FAE=∠ABE,∠D=∠ECF,∠DAF=∠E, ∴△BEA∽△CEF,△DAF∽△CEF. 故选 B. 【点评】本题考查的是相似三角形的判定,熟知有两组角对应相等的两个三角形 相似是解答此题的关键. 6.如图,D 为△ABC 边 BC 上一点,要使△ABD∽△CBA,应该具备下列条件中 的( ) A. = B. = C. = D. = 【考点】相似三角形的判定. 【分析】根据相似三角形的判定问题,题中已有一公共角,再添加对应边比值相 等即可. 【解答】解:当 = 时, 又∵∠B=∠B, ∴△ABD∽△CBA. 故选:C. 【点评】此题主要考查了相似三角形的判定,熟练掌握相似三角形的判定是解题 关键. 7.如图,在△ABC 中,若 DE∥BC, ,DE=3cm,则 BC 的长为( ) A.3cm B.6cm C.9cm D.12cm 【考点】相似三角形的判定与性质. 【分析】首先利用平行线判定两三角形相似,然后利用相似三角形对应边的比等 于相似比求得线段 BC 的长即可. 【解答】解:∵DE∥BC, ∴△ADE∽△ABC, ∵ , ∴ , ∵DE=3cm, ∴ = , 解得:DE=9cm. 故选 C. 【点评】本题考查了相似三角形的判定与性质,解题的关键是根据平行线判定相 似三角形,然后利用相似三角形的对应边的比等于相似比求得相应线段的长. 8.如图,△ABC 中,∠A=78°,AB=4,AC=6.将△ABC 沿图示中的虚线剪开,剪 下的阴影三角形与原三角形不相似的是( ) A. B. C . D. 【考点】相似三角形的判定. 【分析】根据相似三角形的判定定理对各选项进行逐一判定即可. 【解答】解:A、阴影部分的三角形与原三角形有两个角相等,故两三角形相似, 故本选项错误; B、阴影部分的三角形与原三角形有两个角相等,故两三角形相似,故本选项错 误; C、两三角形的对应边不成比例,故两三角形不相似,故本选项正确; D、两三角形对应边成比例且夹角相等,故两三角形相似,故本选项错误. 故选 C. 【点评】本题考查的是相似三角形的判定,熟知相似三角形的判定定理是解答此 题的关键. 9.如图,线段 CD 两个端点的坐标分别为 C(3,3),D(4,1),以原点 O 为位 似中心,在第一象限内将线段 CD 放大为原来的 2 倍后得到线段 AB,则端点 B 的 坐标为( ) A.(6,6) B.(6,8) C.(8,6) D.(8,2) 【考点】平面直角坐标系中的位似变换. 【专题】数形结合. 【分析】利用位似变换是以原点为位似中心,相似比为 k,那么位似图形对应点 的坐标的比等于 k 或﹣k 可得到答案. 【解答】解:因为以原点 O 为位似中心,在第一象限内将线段 CD 放大为原来的 2 倍后得到线段 AB, 所以点 B 的坐标为(4×2,1×2),即(8,2). 故选 D. 【点评】本题考查了位似变换:在平面直角坐标系中,如果位似变换是以原点为 位似中心,相似比为 k,那么位似图形对应点的坐标的比等于 k 或﹣k. 10.关于对位似图形的表述,下列命题正确的有( ) ①相似图形一定是位似图形,位似图形一定是相似图形; ②位似图形一定有位似中心; ③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点, 那么这两个图形是位似图形; ④位似图形上任意一组对应点 P,P′与位似中心 O 的距离满足 OP=k•OP′. A.①②③④ B.②③④ C.②③ D.②④ 【考点】位似图形的性质. 【分析】由位似图形的定义可知:如果两个图形是相似图形,且每组对应点的连 线所在的直线都经过同一个点,那么这两个图形是位似图形;故位似图形一定有 位似中心;且位似图形上任意一组对应点 P,P′与位似中心 O 的距离满足 OP=k•OP′.继而可得位似图形一定是相似图形,但是相似图形不一定是位似图 形. 【解答】解:①位似图形一定是相似图形,但是相似图形不一定是位似图形;故 错误; ②位似图形一定有位似中心;正确; ③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点, 那么这两个图形是位似图形;正确; ④位似图形上任意一组对应点 P,P′与位似中心 O 的距离满足 OP=k•OP′;正 确. 故选 B. 【点评】此题考查了位似图形的性质与定义.注意准确理解位似图形的性质是解 此题的关键. 11.如图,在直角梯形 ABCD 中,DC∥AB,∠DAB=90°,AC⊥BC,AC=BC,∠ABC 的平分线分别交 AD、AC 于点 E,F,则 的值是( ) A. B. C. D. 【考点】平行线分线段成比例. 【专题】计算题. 【分析】作 FG⊥AB 于点 G,由 AE∥FG,得出 = ,求出 Rt△BGF≌Rt△BCF, 再由 AB= BC 求解. 【解答】解:作 FG⊥AB 于点 G, ∵∠DAB=90°, ∴AE∥FG, ∴ = , ∵AC⊥BC, ∴∠ACB=90°, 又∵BE 是∠ABC 的平分线, ∴FG=FC, 在 Rt△BGF 和 Rt△BCF 中, ∴Rt△BGF≌Rt△BCF(HL), ∴CB=GB, ∵AC=BC, ∴∠CBA=45°, ∴AB= BC, ∴ = = = = +1. 故选:C. 【点评】本题主要考查了平行线分线段成比例,全等三角形及角平分线的知识, 解题的关键是找出线段之间的关系,CB=GB,AB= BC 再利用比例式求解. 二、填空题 12.如图,△OAC 和△BAD 都是等腰直角三角形,反比例函数在第四象限经过点 B,若 OA2﹣AB2=8,则 k 的值为 ﹣4 . 【考点】相似三角形的判定与性质. 【分析】设 B 点坐标为(a,b),根据等腰直角三角形的性质得 OA= AC,AB= AD,OC=AC,AD=BD,则 OA2﹣AB2=8 变形为 AC2﹣AD2=4,利用平方差公式得到 (AC+AD)(AC﹣AD)=4,所以(OC+BD)•CD=4,则有 a•b=﹣4,根据反比例函 数图象上点的坐标特征易得 k=﹣4. 【解答】解:设 B 点坐标为(a,b), ∵△OAC 和△BAD 都是等腰直角三角形, ∴OA= AC,AB= AD,OC=AC,AD=BD, ∵OA2﹣AB2=8, ∴2AC2﹣2AD2=8,即 AC2﹣AD2=4, ∴(AC+AD)(AC﹣AD)=4, ∴(OC+BD)•CD=4, ∵点 B 在第四象限, ∴a•b=﹣4, ∴k=﹣4. 故答案为:﹣4. 【点评】本题考查了反比例函数图象上点的坐标特征:反比例函数 y= (k 为常 数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值 k,即 xy=k. 13.已知线段 AB=1,C 是线段 AB 的黄金分割点,且 AC<CB,则 AC 的长度为 . 【考点】黄金分割. 【 分 析 】 根 据 黄 金 分 割 点 的 定 义 , 知 AC 是 较 短 线 段 ; 则 AC=1 ﹣ = . 【解答】解:由于 C 为线段 AB=1 的黄金分割点, 且 AC<CB, 则 AC=1﹣ = . 故本题答案为: . 【点评】理解黄金分割点的概念.熟记黄金比的值进行计算. 14.如图,在△ABC 中,D、E 分别是 AB、BC 上的点,且 DE∥AC,若 S△BDE:S△ CDE=1:4,则 S△BDE:S△ACD= 1:20 . 【考点】相似三角形的判定与性质. 【分析】根据等高三角形面积的比等于底的比和相似三角形面积的比等于相似比 的平方即可解出结果. 【解答】解:∵S△BDE:S△DEC=1:4, ∴BE:EC=1:4, ∴BE:BC=1:5, ∵DE∥AC, ∴△BED∽△BCA, ∴ = = , 设 S△BED=k,则 S△DEC=4k,S△ABC=25k, ∴S△ADC=20k, ∴S△BDE:S△DCA=1:20. 故答案为:1:20. 【点评】本题考查了相似三角形的性质,相似三角形面积的比等于相似比的平方, 注意各三角形面积之间的关系是解题的关键. 15.一块矩形绸布的宽 AB=a m,长 AD=1m,按照图中所示的方式将它裁成相同 的n面矩形彩旗,且使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同, 即,那么 a 的值应当是 . 【考点】相似多边形的性质. 【分析】由裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同,根据相似 多边形的对应边成比例可得: ,继而求得答案. 【解答】解:∵使裁出的每面彩旗的宽与长的比与原绸布的宽与长的比相同, ∴ , ∴a2= , ∴a= . 故答案为: . 【点评】此题考查了相似多边形的性质.注意相似多边形的对应边成比例. 16.如图,小亮在晚上由路灯 A 走向路灯 B,当他走到点 C 时,发现身后他影子 的顶部刚好接触到路灯 A 的底部,当他向前再步行 12m 到达点 D 时,发现身前 他影子的顶部刚好接触到路灯 B 的底部.已知小亮的身高是 1.5m,两个路灯的 高度都是 9m.当小亮走到路灯 B 时,他在路灯 A 下的影长是 3.6 m. 【考点】利用影子测量物体的高度. 【专题】计算题. 【 分 析 】 如 图 , 当 小 亮 走 到 路 灯 B 时 , 他 在 路 灯 A 下 的 影 长 为 BH , CE=DF=BG=1.5m,AM=BN=9m,CD=12m,先证明△ACE∽△ABN 得到 = , 同理可得 = ,则 AC=BD= AB,则 AB+12+ AB=AB,解得 AB=18,接着证 明△HBG∽△HAM,然后利用相似比得到 = ,再利用比例性质求出 BH 即可. 【解答】解:如图,当小亮走到路灯 B 时,他在路灯 A 下的影长为 BH, CE=DF=BG=1.5m,AM=BN=9m,CD=12m, ∵CE∥BN, ∴△ACE∽△ABN, ∴ = ,即 = , 同理可得 = , ∴AC=BD, ∴AC=BD= AB, ∵AC+CD+DB=AB, ∴ AB+12+ AB=AB,解得 AB=18, ∵BG∥AM, ∴△HBG∽△HAM, ∴ = ,即 = ,解得 BH=3.6. 即当小亮走到路灯 B 时,他在路灯 A 下的影长是 3.6m. 故答案为 3.6. 【点评】本题考查了相似三角形的应用:利用视点和盲区的知识构建相似三角形, 用相似三角形对应边的比相等的性质求物体的高度. 三、解答题 17.如图,在 Rt△ABC 中,∠ACB=90°,CD⊥AB,垂足为 D. (1)证明:△ACD∽△CBD; (2)已知 AD=2,BD=4,求 CD 的长. 【考点】相似三角形的判定与性质. 【分析】(1)求出∠CDA=∠ACB=90°,根据有两个角对应相等的两三角形相似得 出△ACD∽△CBD,即可得出答案; (2)根据相似三角形的性质即可得到结论. 【解答】证明:(1)∵∠ACB=90°,CD⊥AB, ∴∠CDA=∠CDB=90°, ∵∠A+∠ACD=∠ACD+∠BCD=90°, ∴∠A=∠BCD, ∴△ACD∽△CBD; (2)由(1)知△ACD∽△CBD, ∴ , ∴CD2=AD•BD=2×4=8, ∴CD=2 . 【点评】本题考查了相似三角形的判定和性质,直角三角形的性质,熟练掌握相 似三角形的判定和性质是解题的关键. 18.如图,AD 是△ABC 的高,点 E,F 在边 BC 上,点 H 在边 AB 上,点 G 在边 AC 上,AD=80cm,BC=120cm. (1)若四边形 EFGH 是正方形,求正方形的面积. (2)若四边形 EFGH 是长方形,长方形的面积为 y,设 EF=x,则 y= ﹣ x2+80x .(含 x 的 代 数 式 ),当 x= 60cm 时 , y 最 大 , 最 大 面 积 是 240cm2 . 【考点】相似三角形的判定与性质. 【分析】(1)根据正方形的对边平行可得 HG∥EF,然后得到△AHG 与△ABC 相 似,根据相似三角形对应高的比等于相似比列出比例式,求出 HG,即可得出正 方形的面积; (2)证出△AEF∽△ABC,得出比例式得出 HE,得出长方形的面积 y 是 x 的二次 函数,再利用二次函数的最值问题进行求解即可. 【解答】解:(1)∵四边形 EFGH 是正方形, ∴HG∥EF,GH=HE=ID, ∴△AHG∽△ABC, ∴AI:AD=HG:BC, ∵BC=120cm,AD=80cm, ∴ , 解得:HG=48cm, ∴正方形 EFGH 的面积=HG2=482=2304(cm2); (2)∵四边形 EFGH 是长方形, ∴HG∥EF, ∴△AEF∽△ABC, ∴AI:AD=HG:BC, 即 , 解得:HE=﹣ x+80, ∴长方形 EFGH 的面积 y=x(﹣ x+80)=﹣ x2+80x=﹣ (x﹣60)2+240, ∵﹣ <0, ∴当 x=60,即 EF=60cm 时,长方形 EFGH 有最大面积,最大面积是 240cm2; 故答案为:﹣ x2+80x,60cm,240cm2. 【点评】本题考查了长方形的性质、正方形的性质、相似三角形的判定与性质以 及二次函数的最值问题;根据相似三角形对应高的比等于相似比列出比例式求出 长方形的边长是解决问题(2)的关键. 19.如图,在直角梯形 ABCD 中,∠ABC=90°,AD∥BC,AD=6,AB=7,BC=8, 点 P 是 AB 上一个动点. (1)当 AP=3 时,△DAP 与△CBP 相似吗?请说明理由. (2)求 PD+PC 的最小值. 【考点】相似三角形的判定与性质. 【分析】(1)由题意可知∠A=∠B=90°,AP=3,PB=4,故此 ,从而可 证明△DAP 与△CBP 相似; (2)作点 D 关于 AB 的对称点 D′,连接 D′C 交 BA 于点 P.过点 D′作 D′E⊥BC, 垂足为 E.依据勾股定理求得 D′C 的长即可. 【解答】解:(1)∵∠ABC=90°,AD∥BC, ∴∠BAD=90°. ∴∠A=∠B=90°. ∵AP=3,AB=7, ∴PB=4. ∴ , . ∴ . ∴△DAP∽△CBP. (2)如图所示:点 D 关于 AB 的对称点 D′,连接 D′C 交 BA 于点 P,过点 D′作 D′E ⊥BC,垂足为 E. ∵点 D 与点 D′关于 AB 对称, ∴PD=D′P. ∴PD+PC=D′P+PC=D′C. 在 Rt△D′EC 中,由勾股定理得:D′C= = =7 . ∴PD+PC 的最小值为 7 . 【点评】本题主要考查的相似三角形的判定、轴对称最短路径问题,掌握本题的 辅助线的作法是解题的关键. 20.如图,在 Rt△ABC 中,∠ABC=90°,点 D 为 BC 边上的点,BE⊥AD 于点 E, 延长 BE 交 AC 于点 F. (1)证明:BE2=AE•DE; (2)若 =1, = 2 ;并说明理由. 【考点】相似三角形的判定与性质. 【分析】(1)根据同角的余角相等可证明∠BAE=∠DBE,根据题意可知∠AEB=∠ DEB,从而可证明△ABE∽△BDE,由相似三角形的性质可证明 BE2=AE•DE; (2)过点 C 作 CG⊥AD,交 AD 的延长线于点 G,由题意可知 BE∥CG,故此△BDE ∽△CDG,由 BD=CD,可知 DE=DG,设 AB=2λ,则 BD=λ,依据锐角三角函数的 定义可求得 AE= ,AD= ,从而可求得 DE=DG= ,故此 EG= λ,由 EF∥CG,可知: . 【解答】解:(1)∵BE⊥AD, ∴∠AEB=∠BED=90°. ∴∠BAE+ABE=90°. ∵∠ABC=90°, ∴∠DBE+∠ABE=90°. ∴∠BAE=∠DBE. ∴△ABE∽△BDE. ∴ . ∴BE2=AE•DE. (2)如图所示:过点 C 作 CG⊥AD,交 AD 的延长线于点 G. ∵BE⊥AD,CG⊥AD, ∴BE∥CG. ∴△BDE∽△CDG. ∴ . ∵BD=CD, ∴DE=DG. 设 AB=2λ,则 BD=λ; ∵∠ABD=90°,BE⊥AD, ∴AD= = . ∵cos∠BAD= = , ∴ . ∴AE= . ∴DE=AD﹣AE= = . ∴EG= . ∵EF∥CG, ∴ =2. 故答案为:2. 【点评】本题主要考查的是相似三角形的性质和判定、勾股定理的应用、锐角三 角函数的定义,掌握本题的辅助线的作法是解题的关键. 第四章 图形的相似测试卷 3 一.选择题 1.若 a:b=2:3,则下列各式中正确的式子是( ) A.2a=3b B.3a=2b C. D. 2.若 x:y=1:3,2y=3z,则 的值是( ) A.﹣5 B.﹣ C. D.5 3.如图,在△ABC 中,DE∥BC,若 = ,则 =( ) A. B. C. D. 4.如图,直线 l1∥l2∥l3,一等腰直角三角形 ABC 的三个顶点 A,B,C 分别在 l1, l2,l3 上,∠ACB=90°,AC 交 l2 于点 D,已知 l1 与 l2 的距离为 1,l2 与 l3 的距离为 3,则 的值为( ) A. B. C. D. 5.若两个相似多边形的面积之比为 1:4,则它们的周长之比为( ) A.1:4 B.1:2 C.2:1 D.4:1 6.)已知矩形 ABCD 中,AB=1,在 BC 上取一点 E,沿 AE 将△ABE 向上折叠,使 B 点落在 AD 上的 F 点,若四边形 EFDC 与矩形 ABCD 相似,则 AD=( ) A. B. C. D.2 7.如图,点 F 在平行四边形 ABCD 的边 AB 上,射线 CF 交 DA 的延长线于点 E, 在不添加辅助线的情况下,与△AEF 相似的三角形有( ) A.0 个 B.1 个 C.2 个 D.3 个 8.如图,点 P 在△ABC 的边 AC 上,要判断△ABP∽△ACB,添加一个条件,不 正确的是( ) A.∠ABP=∠C B.∠APB=∠ABC C. = D. = 9.如图,在△ABC 中,BF 平分∠ABC,AF⊥BF 于点 F,D 为 AB 的中点,连接 DF 延长交 AC 于点 E.若 AB=10,BC=16,则线段 EF 的长为( ) A.2 B.3 C.4 D.5 10.△ABC 与△DEF 的相似比为 1:4,则△ABC 与△DEF 的周长比为( ) A.1:2 B.1:3 C.1:4 D.1:16 11.如图是由边长相同的小正方形组成的网格,A,B,P,Q 四点均在正方形网 格的格点上,线段 AB,PQ 相交于点 M,则图中∠QMB 的正切值是( ) A. B.1 C. D.2 12.如图,在直角坐标系中,有两点 A(6,3),B(6,0),以原点 O 位似中心, 相似比为 ,在第一象限内把线段 AB 缩小后得到线段 CD,则点 C 的坐标为( ) A.(2,1) B.(2,0) C.(3,3) D.(3,1) 二.填空题 13.如果 = = =k(b+d+f≠0),且 a+c+e=3(b+d+f),那么 k= . 14.如图,AB∥CD∥EF,AF 与 BE 相交于点 G,且 AG=2,GD=1,DF=5,那么 的值等于 . 15.如图,在△ABC 中,D 是 AB 边上的一点,连接 CD,请添加一个适当的条 件 ,使△ABC∽△ACD.(只填一个即可) 16.已知矩形 ABCD 中,AB=1,在 BC 上取一点 E,将△ABE 沿 AE 向上折叠,使 B 点落在 AD 上的 F 点.若四边形 EFDC 与矩形 ABCD 相似,则 AD= . 三.解答题 17.如图,在△ABC 中,AB=AC=1,BC= ,在 AC 边上截取 AD=BC,连接 BD. (1)通过计算,判断 AD2 与 AC•CD 的大小关系; (2)求∠ABD 的度数. 18.如图,在△ABC 中,AB=AC,∠A=36°,BD 为角平分线,DE⊥AB,垂足为 E. (1)写出图中一对全等三角形和一对相似比不为 1 的相似三角形; (2)选择(1)中一对加以证明. 19.如图,在平面直角坐标系 xOy 中,直线 y=﹣x+3 与 x 轴交于点 C,与直线 AD 交于点 A( , ),点 D 的坐标为(0,1) (1)求直线 AD 的解析式; (2)直线 AD 与 x 轴交于点 B,若点 E 是直线 AD 上一动点(不与点 B 重合), 当△BOD 与△BCE 相似时,求点 E 的坐标. 20.如图,在△ABC 中,AD 平分∠BAC 交 BC 于点 D.点 E、F 分别在边 AB、AC 上,且 BE=AF,FG∥AB 交线段 AD 于点 G,连接 BG、EF. (1)求证:四边形 BGFE 是平行四边形; (2)若△ABG∽△AGF,AB=10,AG=6,求线段 BE 的长. 21.如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边 DE 与 旗杆顶点 A 在同一直线上,已知 DE=0.5 米,EF=0.25 米,目测点 D 到地面的距离 DG=1.5 米,到旗杆的水平距离 DC=20 米,求旗杆的高度. 22.如图,是一个照相机成像的示意图. (1)如果像高 MN 是 35mm,焦距是 50mm,拍摄的景物高度 AB 是 4.9m,拍 摄点离景物有多远? (2)如果要完整的拍摄高度是 2m 的景物,拍摄点离景物有 4m,像高不变,则 相机的焦距应调整为多少? 答案解析 一.选择题 1.若 a:b=2:3,则下列各式中正确的式子是( ) A.2a=3b B.3a=2b C. D. 【考点】比例的性质. 【分析】根据比例的性质,对选项一一分析,选择正确答案. 【解答】解:A、2a=3b⇒a:b=3:2,故选项错误; B、3a=2b⇒a:b=2:3,故选项正确; C、 = ⇒b:a=2:3,故选项错误; D、 = ⇒a:b=4:3,故选项错误. 故选 B. 【点评】考查了比例的性质.在比例里,两个外项的乘积等于两个内项的乘 积. 2.若 x:y=1:3,2y=3z,则 的值是( ) A.﹣5 B.﹣ C. D.5 【考点】比例的性质. 【专题】计算题. 【分析】根据比例设 x=k,y=3k,再用 k 表示出 z,然后代入比例式进行计算即 可得解. 【解答】解:∵x:y=1:3, ∴设 x=k,y=3k, ∵2y=3z, ∴z=2k, ∴ = =﹣5. 故选:A. 【点评】本题考查了比例的性质,利用“设 k 法”分别表示出 x、y、z 可以使计算 更加简便. 3.如图,在△ABC 中,DE∥BC,若 = ,则 =( ) A. B. C. D. 【考点】平行线分线段成比例. 【分析】直接利用平行线分线段成比例定理写出答案即可. 【解答】解:∵DE∥BC, ∴ = = , 故选 C. 【点评】本题考查了平行线分线段成比例定理,了解定理的内容是解答本题的关 键,属于基础定义或定理,难度不大. 4.(2016•淄博)如图,直线 l1∥l2∥l3,一等腰直角三角形 ABC 的三个顶点 A, B,C 分别在 l1,l2,l3 上,∠ACB=90°,AC 交 l2 于点 D,已知 l1 与 l2 的距离为 1, l2 与 l3 的距离为 3,则 的值为( ) A. B. C. D. 【考点】平行线分线段成比例. 【专题】线段、角、相交线与平行线. 【分析】先作出作 BF⊥l 3,AE⊥l 3,再判断△ACE≌△CBF,求出 CE=BF=3, CF=AE=4,然后由 l2∥l3,求出 DG,即可. 【解答】解:如图,作 BF⊥l3,AE⊥l3, ∵∠ACB=90°, ∴∠BCF+∠ACE=90°, ∵∠BCF+∠CFB=90°, ∴∠ACE=∠CBF, 在△ACE 和△CBF 中, , ∴△ACE≌△CBF, ∴CE=BF=3,CF=AE=4, ∵l1 与 l2 的距离为 1,l2 与 l3 的距离为 3, ∴AG=1,BG=EF=CF+CE=7 ∴AB= =5 , ∵l2∥l3, ∴ = ∴DG= CE= , ∴BD=BG﹣DG=7﹣ = , ∴ = . 故选 A. 【点评】此题是平行线分线段成比例试题,主要考查了全等三角形的性质和判定, 平行线分线段成比例定理,勾股定理,解本题的关键是构造全等三角形. 5.若两个相似多边形的面积之比为 1:4,则它们的周长之比为( ) A.1:4 B.1:2 C.2:1 D.4:1 【考点】相似多边形的性质. 【分析】根据相似多边形的面积之比等于相似比的平方,周长之比等于相似比, 就可求解. 【解答】解:∵两个相似多边形面积比为 1:4, ∴周长之比为 =1:2. 故选:B. 【点评】本题考查相似多边形的性质.相似多边形对应边之比、周长之比等于相 似比,而面积之比等于相似比的平方. 6.已知矩形 ABCD 中,AB=1,在 BC 上取一点 E,沿 AE 将△ABE 向上折叠,使 B 点落在 AD 上的 F 点,若四边形 EFDC 与矩形 ABCD 相似,则 AD=( ) A. B. C. D.2 【考点】相似多边形的性质. 【分析】可设 AD=x,根据四边形 EFDC 与矩形 ABCD 相似,可得比例式,求解即 可. 【解答】解:∵沿 AE 将△ABE 向上折叠,使 B 点落在 AD 上的 F 点, ∴四边形 ABEF 是正方形, ∵AB=1, 设 AD=x,则 FD=x﹣1,FE=1, ∵四边形 EFDC 与矩形 ABCD 相似, ∴ = , = , 解得 x1= ,x2= (负值舍去), 经检验 x1= 是原方程的解. 故选 B. 【点评】考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是根据 四边形 EFDC 与矩形 ABCD 相似得到比例式. 7.如图,点 F 在平行四边形 ABCD 的边 AB 上,射线 CF 交 DA 的延长线于点 E, 在不添加辅助线的情况下,与△AEF 相似的三角形有( ) A.0 个 B.1 个 C.2 个 D.3 个 【考点】相似三角形的判定. 【分析】直接利用平行四边形的性质得出 AD∥BC,AB∥DC,再结合相似三角形 的判定方法得出答案. 【解答】解:∵四边形 ABCD 是平行四边形, ∴AD∥BC,AB∥DC, ∴△AEF∽△CBF,△AEF∽△DEC, ∴与△AEF 相似的三角形有 2 个. 故选:C. 【点评】此题主要考查了相似三角形的判定以及平行四边形的性质,正确掌握相 似三角形的判定方法是解题关键. 8.如图,点 P 在△ABC 的边 AC 上,要判断△ABP∽△ACB,添加一个条件,不 正确的是( ) A.∠ABP=∠C B.∠APB=∠ABC C. = D. = 【考点】相似三角形的判定. 【分析】分别利用相似三角形的判定方法判断得出即可. 【解答】解:A、当∠ABP=∠C 时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项 错误; B、当∠APB=∠ABC 时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误; C、当 = 时,又∵∠A=∠A,∴△ABP∽△ACB,故此选项错误; D、无法得到△ABP∽△ACB,故此选项正确. 故选:D. 【点评】此题主要考查了相似三角形的判定,正确把握判定方法是解题关键. 9.如图,在△ABC 中,BF 平分∠ABC,AF⊥BF 于点 F,D 为 AB 的中点,连接 DF 延长交 AC 于点 E.若 AB=10,BC=16,则线段 EF 的长为( ) A.2 B.3 C.4 D.5 【考点】相似三角形的判定与性质. 【分析】根据直角三角形斜边上中线是斜边的一半可得 DF= AB=AD=BD=5 且∠ ABF=∠BFD,结合角平分线可得∠CBF=∠DFB,即 DE∥BC,进而可得 DE=8,由 EF=DE ﹣DF 可得答案. 【解答】解:∵AF⊥BF, ∴∠AFB=90°, ∵AB=10,D 为 AB 中点, ∴DF= AB=AD=BD=5, ∴∠ABF=∠BFD, 又∵BF 平分∠ABC, ∴∠ABF=∠CBF, ∴∠CBF=∠DFB, ∴DE∥BC, ∴△ADE∽△ABC, ∴ = ,即 , 解得:DE=8, ∴EF=DE﹣DF=3, 故选:B. 【点评】本题主要考查直角三角形的性质和相似三角形的判定与性质,熟练运用 其判定与性质是解题的关键. 10.△ABC 与△DEF 的相似比为 1:4,则△ABC 与△DEF 的周长比为( ) A.1:2 B.1:3 C.1:4 D.1:16 【考点】相似三角形的性质. 【分析】由相似三角形周长的比等于相似比即可得出结果. 【解答】解:∵△ABC 与△DEF 的相似比为 1:4, ∴△ABC 与△DEF 的周长比为 1:4; 故选:C. 【点评】本题考查了相似三角形的性质;熟记相似三角形周长的比等于相似比是 解决问题的关键. 11.如图是由边长相同的小正方形组成的网格,A,B,P,Q 四点均在正方形网 格的格点上,线段 AB,PQ 相交于点 M,则图中∠QMB 的正切值是( ) A. B.1 C. D.2 【考点】相似三角形的性质. 【专题】网格型. 【分析】根据题意平移 AB 使 A 点与 P 点重合,进而得出,△QPB′是直角三角形, 再利用 tan∠QMB=tan∠P= ,进而求出答案. 【解答】解:如图所示:平移 AB 使 A 点与 P 点重合,连接 B′Q, 可得∠QMB=∠P, ∵PB′=2 ,PQ=2 ,B′Q=4 , ∴PB′2+PB′2=B′Q2, ∴△QPB′是直角三角形, ∴tan∠QMB=tan∠P= = =2. 故选:D. 【点评】此题主要考查了勾股定理以及锐角三角函数关系,正确得出△QPB′是直 角三角形是解题关键. 12.如图,在直角坐标系中,有两点 A(6,3),B(6,0),以原点 O 位似中心, 相似比为 ,在第一象限内把线段 AB 缩小后得到线段 CD,则点 C 的坐标为( ) A.(2,1) B.(2,0) C.(3,3) D.(3,1) 【考点】平面直角坐标系中的位似变换. 【分析】根据位似变换的性质可知,△ODC∽△OBA,相似比是 ,根据已知数 据可以求出点 C 的坐标. 【解答】解:由题意得,△ODC∽△OBA,相似比是 , ∴ = ,又 OB=6,AB=3, ∴OD=2,CD=1, ∴点 C 的坐标为:(2,1), 故选:A. 【点评】本题考查的是位似变换,掌握位似变换与相似的关系是解题的关键,注 意位似比与相似比的关系的应用. 二.填空题 13.如果 = = =k(b+d+f≠0),且 a+c+e=3(b+d+f),那么 k= 3 . 【考点】比例的性质. 【分析】根据等比性质,可得答案. 【解答】解:由等比性质,得 k= = =3, 故答案为:3. 【 点 评 】 本 题 考 查 了 比 例 的 性 质 , 利 用 了 等 比 性 质 : = = =k⇒k= = . 14.(2016•济宁)如图,AB∥CD∥EF,AF 与 BE 相交于点 G,且 AG=2,GD=1, DF=5,那么 的值等于 . 【考点】平行线分线段成比例. 【分析】首先求出 AD 的长度,然后根据平行线分线段成比例定理,列出比例式 即可得到结论. 【解答】解:∵AG=2,GD=1, ∴AD=3, ∵AB∥CD∥EF, ∴ = , 故答案为: . 【点评】该题主要考查了平行线分线段成比例定理及其应用问题;解题的关键是 准确找出图形中的对应线段,正确列出比例式求解、计算. 15.如图,在△ABC 中,D 是 AB 边上的一点,连接 CD,请添加一个适当的条件 ∠ACD=∠ABC(答案不唯一) ,使△ABC∽△ACD.(只填一个即可) 【考点】相似三角形的判定. 【专题】开放型. 【分析】相似三角形的判定有三种方法: ①三边法:三组对应边的比相等的两个三角形相似; ②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似; ③两角法:有两组角对应相等的两个三角形相似. 由此可得出可添加的条件. 【解答】解:由题意得,∠A=∠A(公共角), 则可添加:∠ACD=∠ABC,利用两角法可判定△ABC∽△ACD. 故答案可为:∠ACD=∠ABC. 【点评】本题考查了相似三角形的判定,解答本题的关键是熟练掌握三角形相似 的三种判定方法,本题答案不唯一. 16.已知矩形 ABCD 中,AB=1,在 BC 上取一点 E,将△ABE 沿 AE 向上折叠,使 B 点落在 AD 上的 F 点.若四边形 EFDC 与矩形 ABCD 相似,则 AD= . 【考点】相似多边形的性质. 【专题】压轴题. 【分析】可设 AD=x,由四边形 EFDC 与矩形 ABCD 相似,根据相似多边形对应边 的比相等列出比例式,求解即可. 【解答】解:∵AB=1, 设 AD=x,则 FD=x﹣1,FE=1, ∵四边形 EFDC 与矩形 ABCD 相似, ∴ = , = , 解得 x1= ,x2= (不合题意舍去), 经检验 x1= 是原方程的解. 故答案为 . 【点评】本题考查了翻折变换(折叠问题),相似多边形的性质,本题的关键是 根据四边形 EFDC 与矩形 ABCD 相似得到比例式. 三.解答题(共 52 分) 17.(2016•福州)如图,在△ABC 中,AB=AC=1,BC= ,在 AC 边上截取 AD=BC,连接 BD. (1)通过计算,判断 AD2 与 AC•CD 的大小关系; (2)求∠ABD 的度数. 【考点】相似三角形的判定. 【分析】(1)先求得 AD、CD 的长,然后再计算出 AD2 与 AC•CD 的值,从而可得 到 AD2 与 AC•CD 的关系; (2)由(1)可得到 BD2=AC•CD,然后依据对应边成比例且夹角相等的两三角形 相似证明△BCD∽△ABC,依据相似三角形的性质可知∠DBC=∠A,DB=CB,然后 结合等腰三角形的性质和三角形的内角和定理可求得∠ABD 的度数. 【解答】解:(1)∵AD=BC,BC= , ∴AD= ,DC=1﹣ = . ∴AD2= = ,AC•CD=1× = . ∴AD2=AC•CD. (2)∵AD=BC,AD2=AC•CD, ∴BC2=AC•CD,即 . 又∵∠C=∠C, ∴△BCD∽△ACB. ∴ ,∠DBC=∠A. ∴DB=CB=AD. ∴∠A=∠ABD,∠C=∠BDC. 设∠A=x,则∠ABD=x,∠DBC=x,∠C=2x. ∵∠A+∠ABC+∠C=180°, ∴x+2x+2x=180°. 解得:x=36°. ∴∠ABD=36°. 【点评】本题主要考查的是相似三角形的性质和判定、等腰三角形的性质、三角 形内角和定理的应用,证得△BCD∽△ABC 是解题的关键. 18.如图,在△ABC 中,AB=AC,∠A=36°,BD 为角平分线,DE⊥AB,垂足为 E. (1)写出图中一对全等三角形和一对相似比不为 1 的相似三角形; (2)选择(1)中一对加以证明. 【考点】相似三角形的判定. 【分析】(1)利用相似三角形的判定以及全等三角形的判定方法得出符合题意的 答案; (2)利用相似三角形的判定以及全等三角形的判定方法分别得出即可. 【解答】解:(1)△ADE≌△BDE,△ABC∽△BCD; (2)证明:∵AB=AC,∠A=36°, ∴∠ABC=∠C=72°, ∵BD 为角平分线, ∴∠ABD= ∠ABC=36°=∠A, 在△ADE 和△BDE 中 ∵ , ∴△ADE≌△BDE(AAS); 证明:∵AB=AC,∠A=36°, ∴∠ABC=∠C=72°, ∵BD 为角平分线, ∴∠DBC= ∠ABC=36°=∠A, ∵∠C=∠C, ∴△ABC∽△BCD. 【点评】此题主要考查了相似三角形以及全等三角形的判定,正确把握判定方法 是解题关键. 19.(2016•广州)如图,在平面直角坐标系 xOy 中,直线 y=﹣x+3 与 x 轴交于点 C,与直线 AD 交于点 A( , ),点 D 的坐标为(0,1) (1)求直线 AD 的解析式; (2)直线 AD 与 x 轴交于点 B,若点 E 是直线 AD 上一动点(不与点 B 重合), 当△BOD 与△BCE 相似时,求点 E 的坐标. 【考点】相似三角形的性质. 【分析】(1)设直线 AD 的解析式为 y=kx+b,用待定系数法将 A( , ),D (0,1)的坐标代入即可; (2)由直线 AD 与 x 轴的交点为(﹣2,0),得到 OB=2,由点 D 的坐标为(0, 1),得到 OD=1,求得 BC=5,根据相似三角形的性质得到 或 , 代入数据即可得到结论. 【解答】解:(1)设直线 AD 的解析式为 y=kx+b, 将 A( , ),D(0,1)代入得: , 解得: . 故直线 AD 的解析式为:y= x+1; (2)∵直线 AD 与 x 轴的交点为(﹣2,0), ∴OB=2, ∵点 D 的坐标为(0,1), ∴OD=1, ∵y=﹣x+3 与 x 轴交于点 C(3,0), ∴OC=3, ∴BC=5 ∵△BOD 与△BEC 相似, ∴ 或 , ∴ = = 或 , ∴BE=2 ,CE= ,或 CE= , ∵BC•EF=BE•CE, ∴EF=2,CF= =1, ∴E(2,2),或(3, ). 【点评】本题考查了相似三角形的性质,待定系数法求函数的解析式,正确的作 出图形是解题的关键. 20.如图,在△ABC 中,AD 平分∠BAC 交 BC 于点 D.点 E、F 分别在边 AB、AC 上,且 BE=AF,FG∥AB 交线段 AD 于点 G,连接 BG、EF. (1)求证:四边形 BGFE 是平行四边形; (2)若△ABG∽△AGF,AB=10,AG=6,求线段 BE 的长. 【考点】相似三角形的性质. 【专题】综合题. 【分析】(1)根据 FG∥AB,又 AD 平分∠BAC,可证得,∠AGF=∠GAF,从而得: AF=FG=BE,又因为 FG∥AB,所以可知四边形 BGFE 是平行四边形; (2)根据△ABG∽△AGF,可得 ,求出 AF 的长,再由(1)的结论: AF=FG=BE,即可得 BE 的长. 【解答】(1)证明:∵FG∥AB, ∴∠BAD=∠AGF. ∵∠BAD=∠GAF, ∴∠AGF=∠GAF,AF=GF. ∵BE=AF,∴FG=BE, 又∵FG∥BE, ∴四边形 BGFE 为平行四边形.(4 分) (2)解:△ABG∽△AGF, ∴ , 即 , ∴AF=3.6, ∵BE=AF, ∴BE=3.6. 【点评】解决此类题目,要掌握平行四边形的判定及相似三角形的性质. 21.如图,某校数学兴趣小组利用自制的直角三角形硬纸板 DEF 来测量操场旗杆 AB 的高度,他们通过调整测量位置,使斜边 DF 与地面保持平行,并使边 DE 与 旗杆顶点 A 在同一直线上,已知 DE=0.5 米,EF=0.25 米,目测点 D 到地面的距离 DG=1.5 米,到旗杆的水平距离 DC=20 米,求旗杆的高度. 【考点】利用标杆测量物体的高度. 【分析】根据题意可得:△DEF∽△DCA,进而利用相似三角形的性质得出 AC 的 长,即可得出答案. 【解答】解:由题意可得:△DEF∽△DCA, 则 = , ∵DE=0.5 米,EF=0.25 米,DG=1.5m,DC=20m, ∴ = , 解得:AC=10, 故 AB=AC+BC=10+1.5=11.5(m), 答:旗杆的高度为 11.5m. 【点评】此题主要考查了相似三角形的应用,得出△DEF∽△DCA 是解题关键. 22.如图,是一个照相机成像的示意图. (1)如果像高 MN 是 35mm,焦距是 50mm,拍摄的景物高度 AB 是 4.9m,拍 摄点离景物有多远? (2)如果要完整的拍摄高度是 2m 的景物,拍摄点离景物有 4m,像高不变,则 相机的焦距应调整为多少? 【考点】利用镜子测量物体的高度. 【分析】(1)利用相似三角形对应边上的高等于相似比即可列出比例式求解; (2)和上题一样,利用物体的高和拍摄点距离物体的距离及像高表示求相机的 焦距即可. 【解答】解:根据物体成像原理知:△LMN∽△LBA, ∴ . (1)∵像高 MN 是 35mm,焦距是 50mm,拍摄的景物高度 AB 是 4.9m, ∴ , 解得:LD=7, ∴拍摄点距离景物 7 米; (2)拍摄高度是 2m 的景物,拍摄点离景物有 4m,像高不变, ∴ , 解得:LC=70, ∴相机的焦距应调整为 70mm. 【点评】本题考查了相似三角形的应用,解题的关键是根据题意得到相似三角形, 并熟知相似三角形对应边上的高的比等于相似比.查看更多