2019年山东省济南市市中区中考数学二模试卷
2019年山东省济南市市中区中考数学二模试卷
一、选择题(共12小题,每小题4分,满分48分,每小题只有一个选项符合题意)
1. 下列实数中,有理数是( )
A.2 B.34 C.π2 D.3.1435
2. 下列几何体中,俯视图是三角形的是( )
A. B. C. D.
3. 港珠澳大桥总投资1100亿,那么1100用科学记数法表示为( )
A.1.1×103 B.1.1×104 C.11×102 D.0.11×104
4. 在以下节能、回收、绿色食品、节水四个标志中,是轴对称图形的是( )
A. B. C. D.
5. 将一把直尺和一块含30∘和60∘角的三角板ABC按如图所示的位置放置,如果∠CDE=40∘,那么∠BAF的大小为( )
A.10∘ B.15∘ C.20∘ D.25∘
6. 下列运算中,正确的是( )
A.(x2)3=x5 B.x2+2x3=3x5 C.(−ab)3=a3b D.x3⋅x3=x6
7. 不等式组x−12>0,1−2x<3 的解集为( )
A.x>12 B.x<−1 C.−1
−12
8. 如图,点A,B,C在⊙O上,∠ABO=32∘,∠ACO=38∘,则∠BOC等于( )
A.60∘ B.70∘ C.120∘ D.140∘
9. 下表显示的是某种大豆在相同条件下的发芽试验结果:
每批粒数n
100
300
400
600
1000
2000
3000
发芽的粒数m
96
282
382
570
948
1904
2850
发芽的频率mn
0.960
0.940
0.955
0.950
0.948
0.952
0.950
下面有三个推断:
①当n为400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率是0.955;
②随着试验时大豆的粒数的增加,大豆发芽的频率总在0.95附近摆动,显示出一定的稳定性,可以估计大豆发芽的概率是0.95;
③若大豆粒数n为4000,估计大豆发芽的粒数大约为3800粒.
其中推断合理的是( )
A.①②③ B.①② C.①③ D.②③
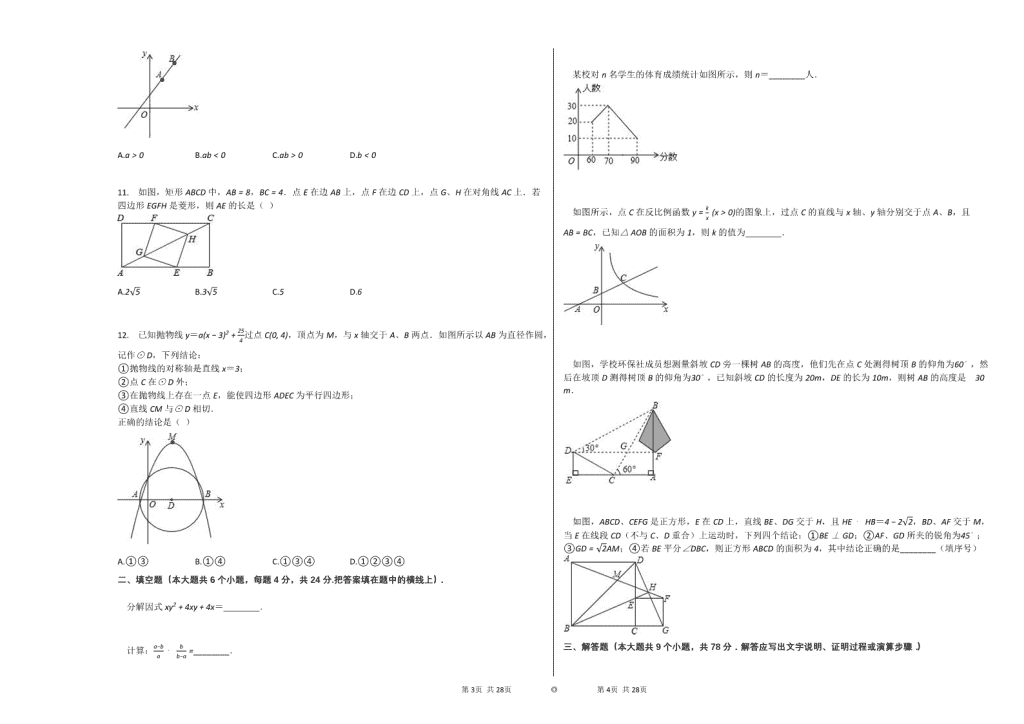
10. A,B两点在一次函数图象上的位置如图所示,两点的坐标分别为A(x+a, y),B(x, y+b),下列结论正确的是( )
A.a>0 B.ab<0 C.ab>0 D.b<0
第25页 共28页 ◎ 第26页 共28页
11. 如图,矩形ABCD中,AB=8,BC=4.点E在边AB上,点F在边CD上,点G、H在对角线AC上.若四边形EGFH是菱形,则AE的长是( )
A.25 B.35 C.5 D.6
12. 已知抛物线y=a(x−3)2+254过点C(0, 4),顶点为M,与x轴交于A、B两点.如图所示以AB为直径作圆,记作⊙D,下列结论:
①抛物线的对称轴是直线x=3;
②点C在⊙D外;
③在抛物线上存在一点E,能使四边形ADEC为平行四边形;
④直线CM与⊙D相切.
正确的结论是( )
A.①③ B.①④ C.①③④ D.①②③④
二、填空题(本大题共6个小题,每题4分,共24分.把答案填在题中的横线上).
分解因式xy2+4xy+4x=________.
计算:a−ba⋅bb−a=________.
某校对n名学生的体育成绩统计如图所示,则n=________人.
如图所示,点C在反比例函数y=kx (x>0)的图象上,过点C的直线与x轴、y轴分别交于点A、B,且AB=BC,已知△AOB的面积为1,则k的值为________.
如图,学校环保社成员想测量斜坡CD旁一棵树AB的高度,他们先在点C处测得树顶B的仰角为60∘,然后在坡顶D测得树顶B的仰角为30∘,已知斜坡CD的长度为20m,DE的长为10m,则树AB的高度是 30 m.
如图,ABCD、CEFG是正方形,E在CD上,直线BE、DG交于H,且HE⋅HB=4−22,BD、AF交于M,当E在线段CD(不与C、D重合)上运动时,下列四个结论:①BE⊥GD;②AF、GD所夹的锐角为45∘;③GD=2AM;④若BE平分∠DBC,则正方形ABCD的面积为4,其中结论正确的是________(填序号)
三、解答题(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)
计算:12+(13)−1−(π−3.14)0−tan60∘.
用公式法解一元二次方程:2x2−7x+6=0.
第25页 共28页 ◎ 第26页 共28页
已知:如图,点B、A、D、E在同一直线上,BD=AE,BC // EF,∠C=∠F.
求证:AC=DF.
学校广播站要招聘一名播音员,擅长诵读的小龙想去应聘,但是不知道是否符合应聘条件,于是在微信上向好朋友亮亮倾诉,如图是他们的部分对话内容.面对小龙的问题,亮亮也犯了难.聪明的你用所学方程知识帮小
龙准确计算一下,他是否符合学校广播站应聘条件?
如图,在Rt△ABC中,∠BAC=90∘,CD平分∠ACB,交AB于点D,以点D为圆心,DA为半径的⊙D与AB相交于点E.
(1)判断直线BC与⊙D的位置关系,并证明你的结论;
(2)若AC=3,BC=5,求BE的长.
某体育老师随机抽取了九年级甲、乙两班部分学生进行一分钟跳绳的测试,并对成绩进行统计分析,绘制了频数分布表和统计图,请你根据图表中的信息完成下列问题:
分组
频数
频率
第一组(0≤x<120)
3
0.15
第二组(120≤x<160)
8
a
第三组(160≤x<200)
7
0.35
第四组(200≤x<240)
b
0.1
(1)频数分布表中a=________,b=________,并将统计图补充完整;
(2)如果该校九年级共有学生360人,估计跳绳能够一分钟完成160或160次以上的学生有多少人?
(3)已知第一组中有两个甲班学生,第四组中只有一个甲班学生,老师随机从这两个组中各选一名学生谈测试体会,则所选两人正好都是甲班学生的概率是多少?
第25页 共28页 ◎ 第26页 共28页
如图,已知直线y=33x与双曲线y=kx交于A,B两点,且点A的横坐标为3.
(1)求k的值;
(2)若双曲线y=kx上点C的纵坐标为3,求△AOC的面积;
(3)在坐标轴上有一点M,在直线AB上有一点P,在双曲线y=kx上有一点N,若以O,M,P,N为顶点的四边形是有一组对角为60∘的菱形,请写出所有满足条件的点P的坐标.
定义:长宽比为n:1(n为正整数)的矩形称为n矩形.下面,我们通过折叠的方式折出一个2矩形,如图a所示.
操作1:将正方形ABEF沿过点A的直线折叠,使折叠后的点B落在对角线AE上的点G处,折痕为AH.
操作2:将FE沿过点G的直线折叠,使点F、点E分别落在边AF、BE上,折痕为CD.则四边形ABCD为2矩形.
(1)证明:四边形ABCD为2矩形;
(2)点M是边AB上一动点.
①如图b,O是对角线AC的中点,若点N在边BC上,OM⊥ON,连接MN.求tan∠OMN的值;
②连接CM,作BR⊥CM,垂足为R.若AB=2,求DR的最小值.
已知,如图,二次函数y=−x2+bx+c的图象经过点A(−1, 0),B(3, 0),点E为二次函数第一象限内抛物线上一动点,EH⊥x轴于点H,交直线BC于点F,以EF为直径的圆⊙M与BC交于点R.
(1)求这个二次函数关系式;
(2)当△EFR周长最大时.
①求此时点E点坐标及△EFR周长;
②点P为⊙M上一动点,连接BP,点Q为BP的中点,连接HQ,求HQ的最大值.
第25页 共28页 ◎ 第26页 共28页
参考答案与试题解析
2019年山东省济南市市中区中考数学二模试卷
一、选择题(共12小题,每小题4分,满分48分,每小题只有一个选项符合题意)
1.
【答案】
D
【考点】
实数
【解析】
直接利用有理数以及无理数的定义分析得出答案.
【解答】
A、2,是无理数,不合题意;
B、34,是无理数,不合题意;
C、π2是无理数,不合题意;
D、3.1435是有理数,符合题意.
2.
【答案】
B
【考点】
简单几何体的三视图
【解析】
根据俯视图是从上边看得到的图形,可得答案.
【解答】
A、圆柱的俯视图是圆,故本选项错误;
B、三棱锥的俯视图是三角形,故本选项正确;
C、长方体的俯视图是长方形,故本选项错误;
D、六棱柱的俯视图是六边形,故本选项错误;
3.
【答案】
A
【考点】
科学记数法--表示较大的数
【解析】
科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正数;当原数的绝对值小于1时,n是负数.
【解答】
1100用科学记数法表示为1.1×103,
4.
【答案】
C
【考点】
轴对称图形
【解析】
根据轴对称图形的概念:如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】
A、不是轴对称图形,故此选项错误;
B、不是轴对称图形,故此选项错误;
C、是轴对称图形,故此选项正确;
D、不是轴对称图形,故此选项错误;
5.
【答案】
A
【考点】
三角形的外角性质
平行线的性质
【解析】
本题主要考查平行线的性质.
【解答】
解:由题意知DE // AF,
∴ ∠AFD=∠CDE=40∘,
∵ ∠B=30∘,
∴ ∠BAF=∠AFD−∠B=40∘−30∘=10∘.
故选A.
6.
【答案】
D
【考点】
幂的乘方与积的乘方
合并同类项
同底数幂的乘法
【解析】
直接利用幂的乘方运算法则以及合并同类项法则以及积的乘方运算法则分别计算得出答案.
【解答】
A、(x2)3=x6,故此选项错误;
B、x2+2x3,无法计算,故此选项错误;
C、(−ab)3=−a3b3,故此选项错误;
D、x3⋅x3=x6,正确.
7.
【答案】
A
【考点】
解一元一次不等式组
【解析】
第25页 共28页 ◎ 第26页 共28页
分别计算出两个不等式的解集,再根据大小小大中间找确定不等式组的解集即可.
【解答】
解:x−12>0①,1−2x<3②,
由①得:x>12,
由②得:x>−1,
不等式组的解集为:x>12.
故选A.
8.
【答案】
D
【考点】
三角形的外角性质
等腰三角形的性质
【解析】
过A、O作⊙O的直径AD,分别在等腰△OAB、等腰△OAC中,根据三角形外角的性质求出θ=2α+2β.
【解答】
解:过A作⊙O的直径,交⊙O于D,
在△OAB中,OA=OB,
则∠BOD=∠OBA+∠OAB=2×32∘=64∘,
同理可得:∠COD=∠OCA+∠OAC=2×38∘=76∘,
故∠BOC=∠BOD+∠COD=140∘.
故选D.
9.
【答案】
D
【考点】
利用频率估计概率
【解析】
根据表中信息,当每批粒数足够大时,频率逐渐接近于0.950,由于试验次数较多,可以用频率估计概率.
【解答】
①当n=400时,发芽的大豆粒数为382,发芽的频率为0.955,所以大豆发芽的概率大约是0.955,此推断错误;
②根据上表当每批粒数足够大时,频率逐渐接近于0.950,所以估计大豆发芽的概率是0.95,此推断正确;
③若n为4000,估计大豆发芽的粒数大约为4000×0.950=3800粒,此结论正确.
10.
【答案】
B
【考点】
一次函数图象上点的坐标特点
一次函数的图象
【解析】
根据一次函数的性质可以判断出a、b的正负,从而可以判断选项中的式子是否正确.
【解答】
由图象可知,
该函数y随x的增大而增大,
∵ A,B两点在一次函数图象上的位置如图所示,两点的坐标分别为A(x+a, y),B(x, y+b),
∴ x+a0,故选项A、D错误,
∴ ab<0,故选项B正确,选项C错误,
故选:B.
11.
【答案】
C
【考点】
菱形的性质
矩形的性质
【解析】
本题考查了菱形的性质,全等三角形的判定和性质,相似三角形的判定和性质.
【解答】
解;连结EF交AC于O,
∵ 四边形EGFH是菱形,
∴ EF⊥AC,OE=OF,
∵ 四边形ABCD是矩形,
∴ ∠B=∠D=90∘,AB // CD,
∴ ∠ACD=∠CAB,
在△CFO与△AOE中,∠FCO=∠OAB∠FOC=∠AOEOF=OE ,
∴ △CFO≅△AOE,
∴ AO=CO,
∵ AC=AB2+BC2=45,
∴ AO=12AC=25,
第25页 共28页 ◎ 第26页 共28页
∵ ∠CAB=∠CAB,∠AOE=∠B=90∘,
∴ △AOE∽△ABC,
∴ AOAB=AEAC,
∴ 258=AE45,
∴ AE=5.
故选C.
12.
【答案】
B
【考点】
二次函数综合题
【解析】
①根据抛物线的解析式即可判定;
②求得AD、CD的长进行比较即可判定,
③过点C作CE // AB,交抛物线于E,如果CE=AD,则根据一组等边平行且相等的四边形是平行四边形即可判定;
④求得直线CM、直线CD的解析式通过它们的斜率进行判定;
【解答】
由抛物线y=a(x−3)2+254可知:抛物线的对称轴x=3,故①正确;
∵ 抛物线y=a(x−3)2+254过点C(0, 4),
∴ 4=9a+254,解得:a=−14,
∴ 抛物线的解析式为y=−14(x−3)2+254,
令y=0,则−14(x−3)2+254=0,解得:x=8或x=−2,
∴ A(−2, 0),B(8, 0);
∴ AB=10,
∴ AD=5,
∴ OD=3
∵ C(0, 4),
∴ CD=OC2+OD2=5,
∴ CD=AD,
∴ 点C在圆上,故②错误;
过点C作CE // AB,交抛物线于E,
∵ C(0, 4),
代入y=−14(x−3)2+254得:4=−14(x−3)2+254,
解得:x=0,或x=6,
∴ CE=6,
∴ AD≠CE,
∴ 四边形ADEC不是平行四边形,故③错误;
由抛物线y=a(x−3)2+254可知:M(3, 254),
∵ C(0, 4),
∴ 直线CM为y=34x+4,直线CD为:y=−43x+4,
∴ CM⊥CD,
∵ CD=AD=5,
∴ 直线CM与⊙D相切,故④正确;
二、填空题(本大题共6个小题,每题4分,共24分.把答案填在题中的横线上).
【答案】
x(y+2)2
【考点】
提公因式法与公式法的综合运用
【解析】
原式提取x,再利用完全平方公式分解即可.
【解答】
原式=x(y2+4y+4)=x(y+2)2,
【答案】
−ba
【考点】
分式的乘除运算
【解析】
利用分式的基本性质结合乘除运算法则化简求出即可.
【解答】
a−ba⋅bb−a=−ba.
【答案】
60
【考点】
折线统计图
【解析】
根据统计图中的数据,可以求得n的值,本题得以解决.
【解答】
由统计图可得,
n=20+30+10=60(人),
【答案】
第25页 共28页 ◎ 第26页 共28页
4
【考点】
一次函数图象上点的坐标特点
反比例函数图象上点的坐标特征
【解析】
根据题意可以设出点A的坐标,从而以得到点C和点B的坐标,再根据△AOB的面积为1,即可求得k的值.
【解答】
解:设点A的坐标为(−a, 0),
∵ 过点C的直线与x轴,y轴分别交于点A,B,且AB=BC,△AOB的面积为1,
∴ 点C(a, ka),
∴ 点B的坐标为(0, k2a),
∴ 12⋅a⋅k2a=1,
解得,k=4.
故答案为:4.
【答案】
30
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
先根据CD=20米,DE=10m得出∠DCE=30∘,故可得出∠DCB=90∘,再由∠BDF=30∘可知∠DBE=60∘,由DF // AE可得出∠BGF=∠BCA=60∘,故∠GBF=30∘,所以∠DBC=30∘,再由锐角三角函数的定义即可得出结论.
【解答】
在Rt△CDE中,
∵ CD=20m,DE=10m,
∴ sin∠DCE=1020=12,
∴ ∠DCE=30∘.
∵ ∠ACB=60∘,DF // AE,
∴ ∠BGF=60∘
∴ ∠ABC=30∘,∠DCB=90∘.
∵ ∠BDF=30∘,
∴ ∠DBF=60∘,
∴ ∠DBC=30∘,
∴ BC=CDtan30=2033=203m,
∴ AB=BC⋅sin60∘=203×32=30m.
【答案】
①②③④
【考点】
全等三角形的性质与判定
正方形的性质
【解析】
①由已知条件可证得△BEC≅△DGC,∠EBC=∠CDG,因为∠BDC+∠DBH+∠EBC=90∘,所以∠BDC+∠DBH+∠CDG=90∘,即BE⊥GD,故①正确;
②若以BD为直径作圆,那么此圆必经过A、B、C、H、D五点,根据圆周角定理即可得到∠AHD=45∘,所以②的结论也是正确的.
③此题要通过相似三角形来解;由②的五点共圆,可得∠BAH=∠BDH,而∠ABD=∠DBG=45∘,由此可判定△ABM∽△DBG,根据相似三角形的比例线段即可得到AM、DG的比例关系;
④若BE平分∠DBC,那么H是DG的中点;易证得△ABH∽△BCE,得BD⋅BC=BE⋅BH,即2BC2=BE⋅BH,因此只需求出BE⋅BH的值即可得到正方形的面积,可先求出BE、EH的比例关系,代入已知的乘积式中,即可求得BE⋅BH的值,由此得解.
【解答】
①正确,证明如下:
∵ BC=DC,CE=CG,∠BCE=∠DCG=90∘,
∴ △BEC≅△DGC,∴ ∠EBC=∠CDG,
∵ ∠BDC+∠DBH+∠EBC=90∘,
∴ ∠BDC+∠DBH+∠CDG=90∘,即BE⊥GD,故①正确;
②由于∠BAD、∠BCD、∠BHD都是直角,因此A、B、C、D、H五点都在以BD为直径的圆上;
由圆周角定理知:∠DHA=∠ABD=45∘,故②正确;
③由②知:A、B、C、D、H五点共圆,则∠BAH=∠BDH;
又∵ ∠ABD=∠DBG=45∘,
∴ △ABM∽△DBG,得AM:DG=AB:BD=1:2,即DG=2AM;
故③正确;
④过H作HN⊥CD于N,连接EG;
若BH平分∠DBG,且BH⊥DG,已知:BH垂直平分DG;
得DE=EG,H是DG中点,HN为△DCG的中位线;
设CG=x,则:HN=12x,EG=DE=2x,DC=BC=(2+1)x;
∵ HN⊥CD,BC⊥CD,
∴ HN // BC,
∴ ∠NHB=∠EBC,∠ENH=∠ECB,
∴ △BEC∽△HEN,则BE:EH=BC:HN=22+2,即EH=BE22+2;
∴ HE⋅BH=BH⋅BE22+2=4−22,即BE⋅BH=42;
∵ ∠DBH=∠CBE,且∠BHD=∠BCE=90∘,
∴ △BDH∽△BCE,得:DB⋅BC=BE⋅BH=42,
即2BC2=42,得:BC2=4,即正方形ABCD的面积为4;
故④正确;
三、解答题(本大题共9个小题,共78分.解答应写出文字说明、证明过程或演算步骤.)
【答案】
原式=23+3−1−3=3+2.
【考点】
零指数幂、负整数指数幂
实数的运算
零指数幂
第25页 共28页 ◎ 第26页 共28页
特殊角的三角函数值
【解析】
先化简二次根式、计算负整数指数幂、零指数幂、代入三角函数值,再计算加减可得.
【解答】
原式=23+3−1−3=3+2.
【答案】
方程2x2−7x+6=0,
这里a=2,b=−7,c=6,
∵ △=49−48=1,
∴ x=7±14,
则x1=2,x2=1.5.
【考点】
解一元二次方程-公式法
【解析】
方程利用公式法求出解即可.
【解答】
方程2x2−7x+6=0,
这里a=2,b=−7,c=6,
∵ △=49−48=1,
∴ x=7±14,
则x1=2,x2=1.5.
【答案】
证明:∵ BD=AE,
∴ BD−AD=AE−AD.
即AB=DE.
∵ BC // EF,
∴ ∠B=∠E.
又∵ ∠C=∠F,
在△ABC和△DEF中,∠B=∠E∠C=∠FAB=DE
∴ △ABC≅△DEF.
∴ AC=DF.
【考点】
全等三角形的性质与判定
【解析】
由已知条件BD=AE可得出AB=DE,再利用AAS定理证明△ABC≅△DEF即可.
【解答】
证明:∵ BD=AE,
∴ BD−AD=AE−AD.
即AB=DE.
∵ BC // EF,
∴ ∠B=∠E.
又∵ ∠C=∠F,
在△ABC和△DEF中,∠B=∠E∠C=∠FAB=DE
∴ △ABC≅△DEF.
∴ AC=DF.
【答案】
设小龙每分钟读x个字,小龙奶奶每分钟读(x−50)个字,
根据题意,得:1050x−50=1300x,
解得:x=260,
经检验,x=260是所列方程的解,并且符合实际问题的意义.
∵ 学校广播站招聘条件是每分钟250−270字,
∴ 小龙符合学校广播站应聘条件.
【考点】
分式方程的应用
【解析】
设小龙每分钟读x个字,小龙奶奶每分钟读(x−50)个字,根据奶奶读了1050个字和小龙读1300个字的时间相同,列出关系式即可得出答案.
【解答】
设小龙每分钟读x个字,小龙奶奶每分钟读(x−50)个字,
根据题意,得:1050x−50=1300x,
解得:x=260,
经检验,x=260是所列方程的解,并且符合实际问题的意义.
∵ 学校广播站招聘条件是每分钟250−270字,
∴ 小龙符合学校广播站应聘条件.
【答案】
解:(1)直线BC与⊙D相切,
理由:过D作DF⊥BC于F,如图,
∴ ∠CFD=∠A=90∘,
∵ CD平分∠ACB,
∴ DA=DF,
∴ 直线BC与⊙D相切;
第25页 共28页 ◎ 第26页 共28页
(2)∵ ∠BAC=90∘,AC=3,BC=5,
∴ AB=BC2−AC2=4.
在Rt△ACD与Rt△FCD中,
AD=DF,CD=CD,
∴ Rt△ACD≅Rt△FCD(HL),
∴ CF=AC=3,
∴ BF=2.
∵ BF是⊙D的切线,
∴ BF2=BA⋅BE,
∴ BE=BF2AB=224=1.
【考点】
切线的判定
切线的性质
勾股定理
直角三角形全等的判定
【解析】
(1)过Q作DF⊥BC于F,根据角平分线的性质得到DA=DF,根据切线的判定定理即可得到结论;
(2)根据勾股定理得到AB=BC2−AC2=4,根据全等三角形的性质得到CF=AC=3,求得BF=2,根据相似三角形的性质即可得到结论.
【解答】
解:(1)直线BC与⊙D相切,
理由:过D作DF⊥BC于F,如图,
∴ ∠CFD=∠A=90∘,
∵ CD平分∠ACB,
∴ DA=DF,
∴ 直线BC与⊙D相切;
(2)∵ ∠BAC=90∘,AC=3,BC=5,
∴ AB=BC2−AC2=4.
在Rt△ACD与Rt△FCD中,
AD=DF,CD=CD,
∴ Rt△ACD≅Rt△FCD(HL),
∴ CF=AC=3,
∴ BF=2.
∵ BF是⊙D的切线,
∴ BF2=BA⋅BE,
∴ BE=BF2AB=224=1.
【答案】
0.4,2
根据题意得:
360×(0.35+0.1)=162(人),
答:跳绳能够一分钟完成160或160次以上的学生有162人;
根据题意画树状图如下:
∵ 共有6种等可能的结果,所选两人正好都是甲班学生的有2种情况,
∴ 所选两人正好都是甲班学生的概率是:26=13.
【考点】
用样本估计总体
列表法与树状图法
频数(率)分布表
【解析】
(1)由统计图易得a与b的值,继而将统计图补充完整;
(2)利用用样本估计总体的知识求解即可求得答案;
(3)首先根据题意画出树状图,然后由树状图求得所有等可能的结果与所选两人正好都是甲班学生的情况,再利用概率公式即可求得答案.
【解答】
a=1−0.15−0.35−0.1=0.4;
∵ 总人数为:3÷0.15=20(人),
∴ b=20×0.1=2(人);
故答案为:0.4,2;
补全统计图得:
根据题意得:
360×(0.35+0.1)=162(人),
答:跳绳能够一分钟完成160或160次以上的学生有162人;
根据题意画树状图如下:
第25页 共28页 ◎ 第26页 共28页
∵ 共有6种等可能的结果,所选两人正好都是甲班学生的有2种情况,
∴ 所选两人正好都是甲班学生的概率是:26=13.
【答案】
解:(1)把点A的横坐标为3代入y=33x,
∴ 其纵坐标为1,
把点(3, 1)代入y=kx,解得:k=3.
(2)∵ 双曲线y=3x上点C的纵坐标为3,
∴ 横坐标为33.
设过A,C两点的直线方程为:y=kx+b,把点(3, 1),(33, 3),代入得:
1=3k+b,3=33k+b,
解得:k=−3,b=4,
∴ y=−3x+4,设y=−3x+4与x轴交点为D,
则D点坐标为(433, 0),
∴ △AOC的面积=S△COD−S△AOD=12×433×3−12×433×1=433.
(3)设P点坐标(a, 33a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60∘,
∵ 以O,M,P,N为顶点的四边形是有一组对角为60∘的菱形,P在直线y=33x上,
当点M只能在y轴上时,
∴ N点的横坐标为a,代入y=3x,解得纵坐标为:3a,
根据OP=NP,即得:|233a|=|3a−33a|,
解得:a=±1.
故P点坐标为:(1, 33)或(−1, −33).
当点M在x轴上时,
同法可得P点坐标(3, 3)或(−3, −3).
则满足条件的点P的坐标为:(1, 33),(−1, −33),(3, 3),(−3, −3).
【考点】
反比例函数与一次函数的综合
待定系数法求反比例函数解析式
反比例函数图象上点的坐标特征
反比例函数系数k的几何意义
【解析】
(1)把点A的横坐标为3代入y=33x求出其纵坐标,然后把A点的坐标代入y=kx求出k即可.
(2)根据纵坐标为3,求出横坐标,再求出过A,C两点的直线方程,然后根据△AOC的面积=S△COD−S△AOD求解即可.
(3)设P点坐标(a, 33a),根据题意,分两种情形①点M只能在横坐标轴上,②M在y轴上时,分别即可求解.
【解答】
解:(1)把点A的横坐标为3代入y=33x,
∴ 其纵坐标为1,
把点(3, 1)代入y=kx,解得:k=3.
(2)∵ 双曲线y=3x上点C的纵坐标为3,
∴ 横坐标为33.
设过A,C两点的直线方程为:y=kx+b,把点(3, 1),(33, 3),代入得:
1=3k+b,3=33k+b,
解得:k=−3,b=4,
∴ y=−3x+4,设y=−3x+4与x轴交点为D,
则D点坐标为(433, 0),
∴ △AOC的面积=S△COD−S△AOD=12×433×3−12×433×1=433.
(3)设P点坐标(a, 33a),由直线AB解析式可知,直线AB与y轴正半轴夹角为60∘,
∵ 以O,M,P,N为顶点的四边形是有一组对角为60∘的菱形,P在直线y=33x上,
当点M只能在y轴上时,
∴ N点的横坐标为a,代入y=3x,解得纵坐标为:3a,
根据OP=NP,即得:|233a|=|3a−33a|,
解得:
第25页 共28页 ◎ 第26页 共28页
a=±1.
故P点坐标为:(1, 33)或(−1, −33).
当点M在x轴上时,
同法可得P点坐标(3, 3)或(−3, −3).
则满足条件的点P的坐标为:(1, 33),(−1, −33),(3, 3),(−3, −3).
【答案】
证明:设正方形ABEF的边长为a,
∵ AE是正方形ABEF的对角线,
∴ ∠DAG=45∘,
由折叠性质可知AG=AB=a,∠FDC=∠ADC=90∘,
则四边形ABCD为矩形,
∴ △ADG是等腰直角三角形,
∴ AD=DG=a2,
∴ AB:AD=a:a2=2:1,
∴ 四边形ABCD为2矩形;
①作OP⊥AB,OQ⊥BC,垂足分别为P,Q,如图b所示:
∵ 四边形ABCD是矩形,∠B=90∘,
∴ 四边形BQOP是矩形.
∴ ∠POQ=90∘,OP // BC,OQ // AB.
∴ OPBC=AOAC,OQAB=COCA,
∵ O为AC中点,
∴ OP=12BC,OQ=12AB,
∵ ∠MON=90∘,
∴ ∠QON=∠POM,
∴ Rt△QON∽Rt△POM,
∴ ONOM=OQOP=ABBC=2,
∴ tan∠OMN=ONOM=2;
②如图c所示:
∵ 四边形ABCD为2矩形,CD=AB=2,
∴ BC=AD=1,
∵ BR⊥CM,
∴ 点R在以BC为直径的圆上,记BC的中点为I,
∴ CI=12BC=12,
∴ DR最小=CD2+CI2−12=(2)2+(12)2−12=32−12=1.
【考点】
四边形综合题
【解析】
(1)先证出∠DAG=45∘,进而判断出四边形ABCD是矩形,再求出AB:AD的值,即可得出结论;
(2)①作OP⊥AB,OQ⊥BC,垂足分别为P,Q,证出四边形BQOP是矩形.得出∠POQ=90∘,OP // BC,OQ // AB.由平行线得出OPBC=AOAC,OQAB=COCA,证出OP=12BC,OQ=12AB,证明Rt△QON∽Rt△POM,得出ONOM=OQOP=ABBC=2,求出tan∠OMN=ONOM=2即可;
②由2矩形的性质得出BC=AD=1,证出点R在以BC为直径的圆上,记BC的中点为I,得出CI=12BC=12,得出DR最小=CD2+CI2−12=1即可.
【解答】
证明:设正方形ABEF的边长为a,
∵ AE是正方形ABEF的对角线,
∴ ∠DAG=45∘,
由折叠性质可知AG=AB=a,∠FDC=∠ADC=90∘,
则四边形ABCD为矩形,
∴ △ADG是等腰直角三角形,
∴ AD=DG=a2,
∴ AB:AD=a:a2=2:1,
∴ 四边形ABCD为2矩形;
①作OP⊥AB,OQ⊥BC,垂足分别为P,Q,如图b所示:
∵ 四边形ABCD是矩形,∠B=90∘,
∴ 四边形BQOP是矩形.
∴ ∠POQ=90∘,OP // BC,OQ // AB.
∴ OPBC=AOAC,OQAB=COCA,
∵ O为AC中点,
∴ OP=12BC,OQ=12AB,
∵ ∠MON=90∘,
∴ ∠QON=∠POM,
∴ Rt△QON∽Rt△POM,
∴ ONOM=OQOP=ABBC=2,
∴ tan∠OMN=ONOM=2;
②如图c所示:
∵ 四边形ABCD为2
第25页 共28页 ◎ 第26页 共28页
矩形,CD=AB=2,
∴ BC=AD=1,
∵ BR⊥CM,
∴ 点R在以BC为直径的圆上,记BC的中点为I,
∴ CI=12BC=12,
∴ DR最小=CD2+CI2−12=(2)2+(12)2−12=32−12=1.
【答案】
用交点式函数表达式得:y=−(x+1)(x−3)=−x2+2x+3;
①∵ ∠CBO=∠FER,∴ △ERF∽△BCO,
∴ △ERF为等腰直角三角形
当△EFR周长最大时,EF最长,
设E(m, −m2+2m+3),F(m, −m+3),
∴ EF=−m2+3m,
当m=32时,
EF=94,E(32, 154),
则Rt△EFR中,ER=FR=928,
∴ △EFR周长为94+942;
②如图,连接OP,点H(32, 0)为OB的中点,
∵ Q是PB的中点,∴ HQ // OP,且HQ=12OP,
∵ EF=94,FH=34,
∴ 点M(32, 218),
∴ OM=BM=3658,
∵ OP≤OM+PM=3658+98,
∴ HQ≤36516+916,
即HQ的最大值大为:36516+916.
【考点】
二次函数综合题
【解析】
(1)用交点式函数表达式,即可求解;
(2)证明△ERF为等腰直角三角形,当△EFR周长最大时,EF最长,EF=−m2+3m,即可求解;②HQ=12OP,利用OP≤OM+PM=3658+98,即可求解.
【解答】
用交点式函数表达式得:y=−(x+1)(x−3)=−x2+2x+3;
①∵ ∠CBO=∠FER,∴ △ERF∽△BCO,
∴ △ERF为等腰直角三角形
当△EFR周长最大时,EF最长,
设E(m, −m2+2m+3),F(m, −m+3),
∴ EF=−m2+3m,
当m=32时,
EF=94,E(32, 154),
则Rt△EFR中,ER=FR=928,
∴ △EFR周长为94+942;
②如图,连接OP,点H(32, 0)为OB的中点,
∵ Q是PB的中点,∴ HQ // OP,且HQ=12OP,
∵ EF=94,FH=34,
∴ 点M(32, 218),
第25页 共28页 ◎ 第26页 共28页
∴ OM=BM=3658,
∵ OP≤OM+PM=3658+98,
∴ HQ≤36516+916,
即HQ的最大值大为:36516+916.
第25页 共28页 ◎ 第26页 共28页